Gemengd elektrisch circuit

We leggen uit wat een gemengd circuit is, de kenmerken, onderdelen, symbolen en geven verschillende voorbeelden

Wat is een gemengd circuit?

Hij gemengd elektrisch circuit Het is er een die elementen bevat die zowel in serie als parallel zijn verbonden, zodat bij het sluiten van het circuit verschillende spanningen en stromen in elk van hen worden vastgesteld.

De circuits zijn ontworpen met een breed scala aan doelstellingen en hun elementen behoren tot twee categorieën: activa en passiva.

De actieve elementen van het circuit zijn generatoren of spanning of stroombronnen, direct of alternatief. Aan de andere kant zijn de passieve elementen de weerstand, de condensatoren of condensatoren en de spoelen. Zowel één als anderen geven verbindingen in serie en parallel toe, evenals combinaties hiervan.

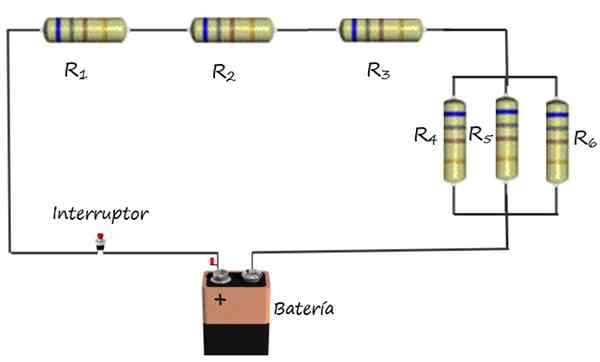
De bovenste figuur toont bijvoorbeeld een gemengde associatie van elektrische weerstanden met een batterij en een schakelaar. Weerstanden r₁, R₂ en r₃ Ze worden geassocieerd in serie, terwijl R weerstanden₄, R₅ en r₆ Ze zijn parallel verbonden.

Andere mogelijke verbindingen, verschillend van seriële parallelle associaties, zijn delta (of driehoek) en ster, vaak gebruikt in elektrische machines die gevoed zijn met een wisselstroom.

Kenmerken van een gemengd circuit

Over het algemeen wordt het volgende waargenomen in een gemengd circuit:

• Circuitvoer kan via een directe generator (batterij) of alternatief zijn.
• Er wordt aangenomen dat de kabels of draden die de verschillende elementen verenigen, geen huidige weerstand bieden.
• Zowel spanning als stroom kunnen constant of variabel zijn in de tijd. Kapitaalletters worden gebruikt om constante waarden aan te duiden en kleine letters wanneer variabel.
• In puur resistieve gemengde circuits is de stroom door reeksweerstanden hetzelfde, terwijl het in parallelle weerstanden in het algemeen anders is. Om de stroom en de spanning door elke weerstand te berekenen, wordt het circuit meestal gereduceerd tot een unieke weerstand, genaamd equivalente weerstand of r_eq .

Het kan u van dienst zijn: Vectoraftrekking: grafische methode, voorbeelden, oefeningen

Seriesweerstand

Weerstanden parallel

• Als het circuit uit N -condensatoren bestaat, wanneer de equivalente capaciteit C in serie is geassocieerd_eq resultaat:

Serie -condensatoren

Parallelle condensatoren

• De spoelen of inductoren volgen dezelfde associatieregels als weerstand. Dus wanneer u een Series -spoelvereniging wilt verminderen om de equivalente inductie L te verkrijgen_eq, De volgende formules worden gebruikt:

Seriële inductoren

Inductoren parallel

• Om de gemengde circuits op te lossen met weerstanden, worden de OHM -wet en de Kirchoff -wetten gebruikt. In eenvoudige resistieve circuits is de wet van Ohm voldoende, maar voor complexere netwerken is het noodzakelijk aanwezig.

Relatie tussen spanning en stroom

Afhankelijk van het circuitelement is er een verband tussen de spanning of spanning door het element met de intensiteit van de stroom die erdoorheen gaat:

Weerstand r

De wet van Ohm wordt gebruikt:

v_R(t) = r ∙ i_R(T)

Condensator C

Inductantie l

Delen van een gemengd circuit

In een elektrisch circuit worden de volgende delen onderscheiden:

Knoop

Unie -punt tussen twee of meer geleidende draden die enkele actieve of verplichtingen van het circuit verbinden.

Tak

Elementen, of het nu actieve of aansprakelijkheden zijn, die tussen twee opeenvolgende knopen zijn.

Mazen

Gesloten gedeelte van het circuit gereisd zonder tweemaal door hetzelfde punt te passeren. Het kan al dan niet een spanning of stroomgenerator hebben.

Kirchoff -wetten of regels

Kirchoff -regels zijn van toepassing, zowel of stromingen als spanningen constant zijn of dat ze afhankelijk zijn van de tijd. Hoewel ze meestal wetten worden genoemd, zijn het eigenlijk regels om instandhoudingsprincipes toe te passen op elektrische circuits.

Kan u van dienst zijn: Solid State Fysica: eigenschappen, structuur, voorbeelden

Eerste regel

Het stelt het principe van behoud van de belasting vast en wijst erop dat de som van de huidige intensiteiten die een knoop aangaan, gelijkwaardig aan de som van de intensiteiten die eruit komen:

∑ i_Ingang = ∑ i_Uitgang

Tweede regel

Bij deze gelegenheid wordt het principe van energiebesparing vastgesteld, wanneer het stelt dat de algebraïsche som van spanningen in een gesloten deel van het circuit (mesh) nul is.

∑ vi = 0

Symbolen

Om de analyse van de circuits te vergemakkelijken, worden de volgende symbolen gebruikt:

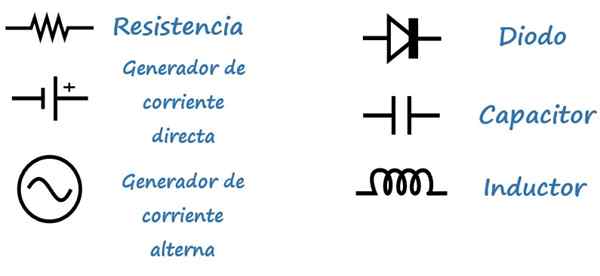
Voorbeelden van gemengde circuit

voorbeeld 1

Teken het gemengde circuit van de startfiguur compact, met behulp van de hierboven beschreven symbolen.

Antwoord

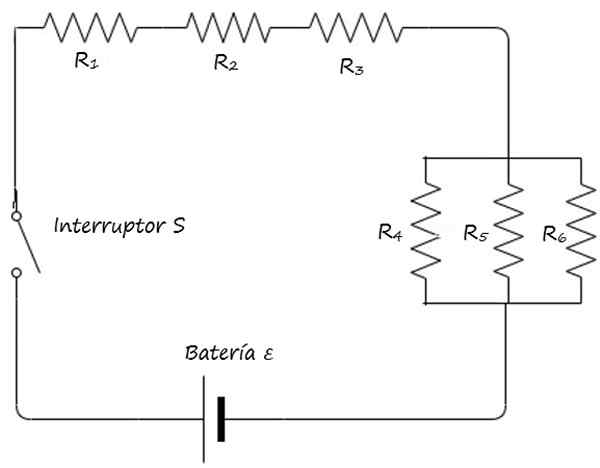
Voorbeeld 2

In het circuit van voorbeeld 1 heeft u de volgende waarden voor weerstanden en batterij:

R₁ = 50 Ω; R₂ = 100 Ω; R₃ = 75 Ω, r₄ = 24 Ω, r₅ = 48 Ω; R₆ = 48 Ω; ε = 100 V

Voor het getoonde circuit wordt de batterij als ideaal beschouwd, dat wil zeggen dat hij geen interne weerstand heeft. Meestal hebben echte batterijen een kleine interne weerstand die in serie met de batterij wordt getekend en hetzelfde wordt behandeld als de andere weerstanden in het circuit.

Bereken het volgende:

• a) De equivalente weerstand van het circuit.
• b) De waarde van de stroom die uit de batterij komt.
• c) De spanningen en stromen in elk van de weerstanden.

Antwoord op

De eerste groep weerstanden: r₁ = 50 Ω; R₂ = 100 Ω; R₃ = 75 Ω zijn in serie verbonden, daarom is de equivalente weerstand R₁₂₃:

R₁₂₃ = R₁ + R₂ + R₃ = 50 Ω + 100 Ω + 75 Ω = 225 Ω

Het kan u van dienst zijn: Derde wet van thermodynamica: formules, vergelijkingen, voorbeelden

Wat betreft de R -weerstandsgroep₄ = 24 Ω, r₅ = 48 Ω; R₆ = 48 Ω, zijn parallel aangesloten en de overeenkomstige formule moet worden toegepast:

 De wederzijdse of omgekeerde van het vorige resultaat is de equivalente weerstand voor de groep:

R₄₅₆ = 12 Ω

Het verkregen vereenvoudigde circuit wordt weergegeven in de volgende grafiek, bestaande uit twee series weerstanden met de batterij of batterij. Deze twee weerstanden worden toegevoegd om de equivalente weerstand van het oorspronkelijke R -circuit te vinden_eq:

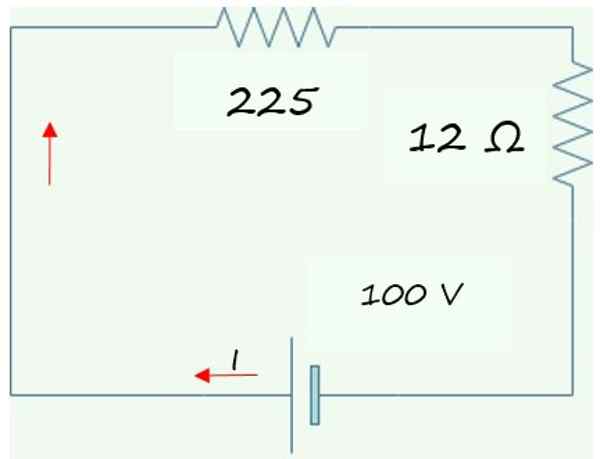
R_eq= 225 Ω + 12 Ω = 237 Ω

Antwoord B

De stroom die de batterij verlaat (volgens de conventie wordt altijd getekend door de positieve pool) wordt berekend met het vereenvoudigde circuit, dat bestaat uit de equivalente weerstand R_eq In serie met de batterij, waarop de wet van Ohm wordt toegepast:

ε = i · r

I = ε / r = 100 V / 237 Ω = 0.422 a

Antwoord C

Spanningen en stromingen in elk van de SA -weerstanden berekenen volgens de wet van Ohm. Het eerste dat wordt waargenomen, is dat de stroom die uit de batterij komt, de weerstanden R volledig kruist R₁ , R₂ en r₃ En in plaats daarvan wordt het gedeeld door R te kruisen₄ , R₅ en r₆.

De spanningen v₁, V₂ en v₃ Zijn:

V₁  = 0.422 A × 50 Ω = 21.1 V
V₂  = 0.422 a × 100 Ω = 42.2 V
V₃  = 0.422 a × 75 Ω = 31.7 V

Voltajes V van zijn kant₄, V₅ en v₆ Ze hebben dezelfde waarde, omdat de weerstanden parallel zijn:

V₄ = V₅ = V₆ = 0.422 a × 12 Ω = 5.06 V

En de respectieve stromingen zijn:

Je₄ = 5.06 V / 24 Ω = 0.211 a

Je₅ = I₆ = 5.06 V / 48 Ω = 0.105 a

Merk op dat door I₄, Je₅ en ik₆ De totale stroom die uit de batterij komt, wordt opnieuw verkregen.