Zwaartepunt eigenschappen, berekening, voorbeelden

Hij zwaartekrachtcentrum van een meetbaar lichaam lichaam is het punt waar het gewicht wordt beschouwd als toegepast. Het is daarom een ​​van de belangrijkste concepten van statische.

De eerste benadering in problemen met de elementaire fysica is om aan te nemen dat elk object zich als een specifieke massa gedraagt, dat wil zeggen dat het dimensies mist en de hele massa op één punt is geconcentreerd. Dit is geldig voor een doos, een auto, een planeet of een subatomair deeltje. Dit model staat bekend als deeltjesmodel.

Figuur 1. In de hoogte springt de atleet ze zodat het zwaartepunt zich buiten het lichaam bevindt. Bron: Pixabay

Natuurlijk is dit een aanpak, die voor veel toepassingen zeer goede resultaten oplevert. Het is geen gemakkelijke taak om het individuele gedrag van de duizenden en miljoenen deeltjes te overwegen die elk object zou kunnen bevatten.

Er moeten echter rekening worden gehouden met de echte dimensies van dingen als u wilt. Omdat we zich meestal in de directe omgeving van de aarde bevinden, is de altijd huidige kracht op elk lichaam precies het gewicht.

[TOC]

Overwegingen om het zwaartepunt te vinden 

Als er rekening wordt gehouden met de lichaamsgrootte, waar het gewicht specifiek wordt toegepast? Als u willekeurig een continu object heeft, is het gewicht een Gedistribueerde kracht tussen elk van zijn samenstellende deeltjes.

Laat deze deeltjes m₁, M₂, M₃... elk van hen ervaart de overeenkomstige zwaartekracht M m ervaart₁g, m₂g, m₃G ..., allemaal parallel. Dit is zo, omdat het zwaartekrachtveld van de aarde in de overgrote meerderheid van de gevallen als constant wordt beschouwd, gezien het feit dat objecten klein zijn in vergelijking met de grootte van de planeet en dicht bij het oppervlak zijn.

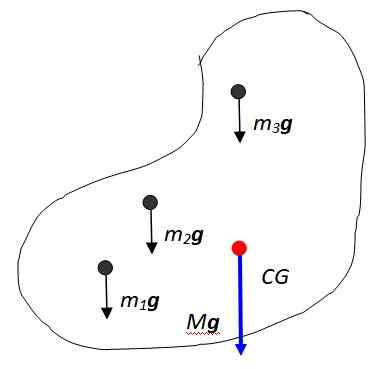Figuur 2. Het gewicht van het object is een gedistribueerde massa. Bron: zelf gemaakt.

De vector som van deze krachten resulteert in het gewicht van het object, toegepast op het punt dat het zwaartepunt wordt aangeduid als CG, dat vervolgens samenvalt met de Massacentrum. Het massacentrum is op zijn beurt het punt waar de hele massa kan worden beschouwd als geconcentreerd.

Het resulterende gewicht heeft een grootte Mg waar M Het is de totale massa van het object, en natuurlijk wordt het verticaal gericht naar het midden van de aarde. Sumory -notatie is nuttig om het totale lichaam van het lichaam uit te drukken:

Symmetrische en homogene objecten, die gelijkwaardig zijn aan hun dichtheid die uniform is, hebben hun zwaartepunt in het geometrische centrum: kubussen, parallellepipeds, ringen, banden of bollen.

Het zwaartepunt komt niet altijd overeen met een materiaalpunt. De CG van een hoepel bevindt zich bijvoorbeeld in zijn geometrische centrum, waar er geen deeg zelf is. Toch, als u de krachten wilt analyseren die op een hoepel werken, moet het gewicht op dit precieze punt worden toegepast.

In welke gevallen waarin het object willekeurig is, als het homogeen is, kan het massacentrum nog steeds worden berekend door de zwaartepunt o Baricentro van de figuur.

Kan je dienen: Mercury (planeet)

Hoe wordt het zwaartepunt berekend??

In principe Als het zwaartepunt (CG) en het massacentrum (CM) samenvallen wanneer het zwaartekrachtveld uniform is, kan de CM worden berekend en erop worden aangebracht.

Overweeg twee gevallen: de eerste is er een waarin de massadistributie discreet is; dat wil zeggen, u kunt elke massa tellen die het systeem vormt en een nummer I toewijzen, zoals in het vorige voorbeeld is gedaan.

De coördinaten van het massamiddelpunt voor een discrete massadistributie zijn: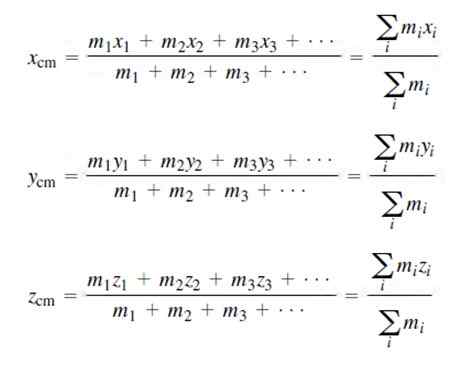

Natuurlijk is de som van alle massa's gelijk aan de totale massa van het M -systeem, zoals hierboven aangegeven.

De drie vergelijkingen worden teruggebracht tot een compacte vorm bij het overwegen van de vector r_cm o Positievector van het massacentrum:

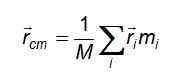
En in het geval van een continue massaverdeling, waarbij de deeltjes van differentiële grootte zijn en niet kunnen worden onderscheiden om ze te tellen, wordt de som vervangen door een integrale die wordt gemaakt over het volume dat wordt bezet door het object in kwestie:

Waar R Het is de positievector van een differentiële massa DM En de definitie van masserdichtheid om het massale differentieel uit te drukken is gemaakt DM opgenomen in een volumeverschil Dv:

De dichtheid van het object kan constant zijn, in welk geval het uit de integraal komt, of een functie is van de ruimtelijke coördinaten en we moeten de afhankelijkheid ervan weten (x, y, z) om de integrale op te lossen.

Eigenschappen

Enkele belangrijke overwegingen over het massacentrum zijn de volgende:

- Hoewel een referentiesysteem vereist is om posities vast te stellen, hangt het massamiddelpunt niet af van de keuze die van het systeem is gemaakt, omdat het een eigenschap van het object is.

- Wanneer het object een as of een symmetrievlak heeft, bevindt het massacentrum zich op de as of het vlak. Profiteer van deze omstandigheid, bespaart de berekeningstijd.

- Alle externe krachten die op het object werken, kunnen op het massacentrum worden toegepast. Het volgen van het spoor van dit punt geeft een globaal idee van de beweging van het object en vergemakkelijkt het werk van het bestuderen van zijn gedrag.

-Het zwaartepunt van een lichaam vinden in een statisch evenwicht

Stel dat het lichaam van de vorige figuur in de statische balans is.

figuur 3. Schema om het gewichtskoppel te berekenen ten opzichte van Point of.

Het moment van netto torsie ten opzichte van O, volgens figuur 3 is: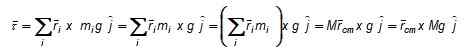Een kracht f uitgeoefend verticaal in het midden van de zwaartekracht (of ook boven of onder, op de as die erdoorheen gaat) zou een tegenovergestelde torsie produceren die de rotatie van het object zou voorkomen en de rotatiebalans zou behouden. De grootte van F wordt gekozen zodat het object ook niet wordt overgedragen en op deze manier zullen we het in statisch evenwicht hebben.

Kan u van dienst zijn: golvende optica

-Opgelost voorbeeld

Een dunne staaf uniform materiaal heeft een lengte van 6 m en weegt 30 n. Aan het einde is een 50 N west en een van de 20 n aan de rechterkant opgehangen. Vind: a) de grootte van de stijgende kracht die nodig is om de balans van de staaf te handhaven, b) het zwaartepunt van de set.

Oplossing

Het krachtenschema wordt getoond in de volgende figuur. Het gewicht van de balk wordt aangebracht in het zwaartepunt, dat samenvalt met zijn geometrische centrum. De enige dimensie van de balk is de lengte in rekening gebracht, omdat de verklaring informeert dat deze dun is.

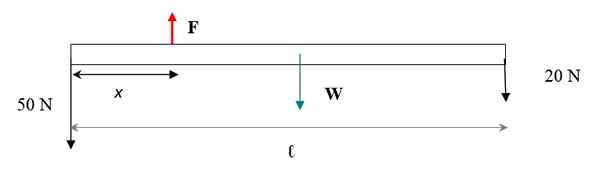Figuur 4. Pàra La Barra Diagram.

Om het bar + gewichtssysteem in de vertaalbalans te blijven, moet de som van de krachten nul zijn. De krachten zijn verticaal, als we overwegen met een bord + en omlaag met een bord - dan:

F- 50- 20-30 N = 0

F = 100 n

Deze kracht garandeert de balans van vertaling. Het nemen van de momenten van torsie van alle krachten met betrekking tot een as die door het linkeruiteinde van het systeem gaat en de definitie toepast:

t = r x f

De momenten van al deze krachten ten opzichte van het geselecteerde punt staan ​​loodrecht op het vlak van de balk:

T_F = xf = 100x

T_W = -(l/2) mg = -3m . 30 n = -90 n.M

T₁ = 0 (omdat de kracht van 50 N door de geselecteerde draaias gaat en geen moment uitoefent)

T₂ = -Lf₂ = 6 m . 20 n = -120 n.M

Daarom:

100 x -90 -120 n.M = 0

x = 2.10 m

Het zwaartepunt van de barbalk + gewichten bevindt zich op 2.10 meter vanaf het linkeruiteinde van de bar.

Verschil met het massamiddelpunt

Het zwaartepunt valt samen met het massamiddelpunt, zoals aangegeven, zolang het land van het land van het land constant is voor alle punten van het object dat moet worden overwogen. Het zwaartekrachtveld van de aarde is niets anders dan de goed bekende en vertrouwde waarde van g = 9.8 m/s² verticaal gericht.

Hoewel de waarde van g variaties met breedtegraad en hoogte ervaart, hebben ze meestal geen invloed op objecten waarover de meeste tijden worden behandeld. Heel anders zou zijn als het wordt beschouwd als een groot lichaam in de buurt van de aarde, bijvoorbeeld een asteroïde die dicht bij de planeet zou komen.

De asteroïde heeft zijn eigen massacentrum, maar het zwaartepunt zou hier niet langer mee moeten samenvallen, sindsdien G Het zou waarschijnlijk aanzienlijke variaties in grootte ervaren, gezien de grootte van de asteroïde en dat de gewichten van elk deeltje mogelijk niet parallel zijn.

Een ander fundamenteel verschil is dat het massacentrum is, ongeacht of er een kracht wordt genoemd, wordt het toegepaste gewicht op het object genoemd. Het is een intrinsieke eigenschap van het object die onthult hoe zijn massa wordt verdeeld in relatie tot zijn geometrie.

Kan u van dienst zijn: wat is de diëlektrische constante?

Het massacentrum bestaat zowel als er gewicht wordt toegepast alsof het niet is. En bevindt zich in dezelfde positie, hoewel het object wordt overgebracht naar een andere planeet waarin het zwaartekrachtveld anders is.

Aan de andere kant is het zwaartepunt duidelijk gekoppeld aan de toepassing van gewicht, zoals we in de vorige paragrafen hebben kunnen waarderen.

M het zwaartekracht voorbeelden

Zwaartepunt van onregelmatige objecten

Het is heel gemakkelijk om erachter te komen waar het zwaartepunt van een onregelmatig object is als een beker. Eerst wordt het aan elk punt gesuspendeerd en van daaruit wordt een verticale lijn getekend (in figuur 5 is het de Fuchsia -lijn in de linker afbeelding).

Dan wordt het opgehangen aan een ander punt en wordt een nieuwe verticale (turquoise lijn in de rechterafbeelding) getekend. De kruising van beide lijnen is het zwaartepunt van de beker.

Figuur 5 . CG -locatie van een beker. Bron: Modified Pixabay.

Balans van objecten

Laten we de stabiliteit van een vrachtwagen analyseren die langs de weg circuleert. Wanneer het zwaartepunt zich boven de basis van de vrachtwagen bevindt, zal het niet gieten. De afbeelding links is de meest stabiele positie.

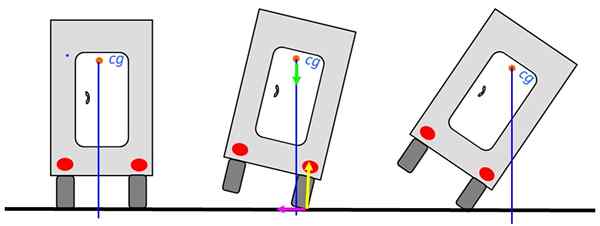Figuur 6. Truckbalans. Bron: zelf gemaakt.

Zelfs wanneer de vrachtwagen naar rechts leunt, kan terugkeren naar de stabiele evenwichtspositie, zoals bij de tekening van het medium, omdat de verticaal nog steeds door de basis gaat. Wanneer deze lijn echter buiten de truck gaat, draait de vrachtwagen.

Het diagram toont de krachten op het ondersteuningspunt: het normale in geel, het gewicht in groen en de statische wrijving links in Fuchsia. Normaal en Rubb. Daarom zullen ze niet bijdragen aan het dumpen van de vrachtwagen.

Het gewicht blijft bestaan, die een moment van torsie uitoefent, gelukkig in de anti -horaire zin en dat heeft de neiging om terug te keren naar de vrachtwagen naar zijn evenwichtspositie. Merk op dat de verticale lijn door het steunoppervlak gaat, dat is de band.

Wanneer de vrachtwagen zich in de positie van uiterste rechts bevindt, verandert de tijd van torsie van gewicht en wordt in een gespannen richting. Niet in staat zijn om op een ander moment tegen te gaan, zal de vrachtwagen gieten.

Referenties

1. Bauer, W. 2011. Fysica voor engineering en wetenschappen. Deel 1. MC Graw Hill.  247-253.
2. Giancoli, D.  2006. Fysica: principes met toepassingen. 6e ... Ed Prentice Hall. 229-238.
3. Resnick, r. (1999). Fysiek. Vol. 1. 3e ed. in het Spaans. Continental Editorial Company s.NAAR. van C.V. 331-341.
4. Rex, a. 2011. Fundamentals of Physics. Pearson.146-155.
5. Sears, Zemansky. 2016. Universitaire natuurkunde met moderne natuurkunde. 14e. ED. Deel 1.340-346.