Punctuele laadeigenschappen en Coulomb -wetgeving

A Punctuele belasting, In de context van elektromagnetisme is het die elektrische lading van zo kleine dimensies, die als een punt kunnen worden beschouwd. Elementaire deeltjes met elektrische lading, proton en elektronen zijn bijvoorbeeld zo klein dat hun afmetingen in tal van toepassingen kunnen worden weggelaten. Bedenk dat een lading punctueel is, vergemakkelijkt het werk van het berekenen van de interacties en het begrijpen van de elektrische eigenschappen van de zaak.

Elementaire deeltjes zijn niet de enige die specifieke belastingen kunnen zijn. De geïoniseerde moleculen kunnen ook zijn, de geladen bollen die Charles vroeger. Coulomb (1736-1806) in zijn experimenten en zelfs hetzelfde land. Allen kunnen worden beschouwd als specifieke belastingen, zolang we ze op afstanden zien die veel groter zijn dan de grootte van het object.

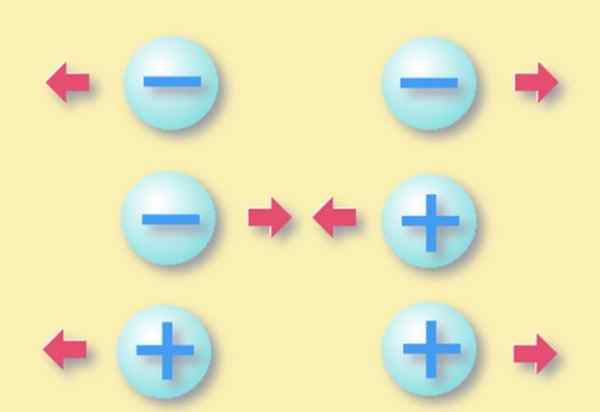
Figuur 1. De specifieke belastingen van hetzelfde teken worden afgestoten, terwijl het tegenovergestelde teken wordt aangetrokken. Bron: Wikimedia Commons.

Omdat alle lichamen van elementaire deeltjes zijn gemaakt, is elektrische lading een inherente eigenschap van materie, net als de massa. U kunt geen elektron zonder massa hebben, en niet zonder load.

[TOC]

Eigenschappen

Voor zover we vandaag weten, zijn er twee soorten elektrische lading: positief en negatief. De elektronen hebben een negatieve typebelasting, terwijl de protonen het positief hebben.

Er worden een ladingen van hetzelfde teken afgestoten, terwijl het tegenovergestelde teken wordt aangetrokken. Dit is geldig voor elk elektrische lading, punctueel of gedistribueerd over een object van meetbare afmetingen.

Bovendien vonden zorgvuldige experimenten dat de protonbelasting en het elektron exact dezelfde grootte hebben.

Een ander zeer belangrijk punt om te overwegen is dat de elektrische lading is gekwantiseerd. Tot op heden zijn geïsoleerde elektrische belastingen niet minder gevonden dan de elektronenbelasting. Het zijn allemaal veelvouden hiervan.

Ten slotte wordt de elektrische lading behouden. Met andere woorden, de elektrische lading wordt niet gecreëerd, noch wordt vernietigd, maar kan worden overgedragen van het ene object naar het andere. Op deze manier, als het systeem geïsoleerd is, blijft de totale belasting constant.

Kan u van dienst zijn: 21 belangrijke gebeurtenissen in de natuurkunde

Elektrische ladingseenheden

De eenheid voor elektrische lading in het internationale systeem van eenheden (SI) is Coulomb, afgekort met een Capital C, ter ere van Charles. Coulomb (1736-1806), die de wet ontdekte die zijn naam draagt ​​en de interactie beschrijft tussen twee specifieke ladingen. Later zullen we over haar praten.

De elektroneneleverkleding, die de kleinst mogelijke is die van aard kan worden geïsoleerd, heeft een omvang van:

En^- = 1.6 x 10 ^-16 C

Coulomb is een vrij grote eenheid, dus submultiples worden vaak gebruikt:

-1 Mili C = 1 MC = 1 x 10^-3 C

-1 Micro C = 1 μC = 1 x 10^-6 C

-1 nano c = 1 nc = 1 x 10^-9 C

En zoals we eerder hebben vermeld, het teken van En^- Het is negatief. De protonbelasting heeft exact dezelfde grootte, maar met een positief teken.

De tekenen zijn een kwestie van conventie, dat wil zeggen, er zijn twee soorten elektriciteit en het is noodzakelijk om ze te onderscheiden, daarom is de ene toegewezen teken (-) en het andere teken (+). Benjamin Franklin heeft deze aanduiding gemaakt en kondigde ook het principe van de belastingbehoud uit.

Voor Franklin's tijd was de interne structuur van het atoom nog onbekend, maar Franklin had opgemerkt dat een zijden gewreven glazen balk elektrisch was geladen, die dit soort elektriciteit positief noemde.

Elk object dat zich tot dergelijke elektriciteit aangetrokken voelde, had een negatief teken. Nadat het elektron was ontdekt, werd waargenomen dat de geladen glazen staaf ze aantrok, en dit is hoe de elektronenbelasting negatief was.

Coulomb Law voor specifieke belastingen

Aan het einde van de 18e eeuw wijdde Coulomb, een ingenieur van het Franse leger, veel tijd om de eigenschappen van de materialen te bestuderen, de krachten die op de stralen en de wrijvingsmacht werken.

Maar het wordt meer onthouden door de wet die zijn naam draagt ​​en de interactie beschrijft tussen twee specifieke elektrische ladingen.

Kan u van dienst zijn: magnetisme: magnetische eigenschappen van materialen, gebruik

Laat twee elektrische ladingen Q₁ En Q₂. Coulomb bepaalde dat de kracht tussen hen, al uit aantrekkingskracht of afstoting, recht evenredig was met het product van beide ladingen, en omgekeerd evenredig met het kwadraat van de afstand daartussen.

Wiskundig:

F∝ q₁ . Q₂ / R²

In deze vergelijking, F vertegenwoordigt de omvang van de kracht en R Het is de afstand die de belastingen scheidt. Gelijkheid vereist een evenredigheidsconstante, die elektrostatische constante wordt genoemd en wordt aangeduid als k_En.

Dus:

F = K. Q₁ . Q₂ /R²

Coulomb ontdek ook dat de kracht was gericht langs de lijn die zich bij de ladingen voegt. Dan ja R Het is de eenheidsvector langs die lijn, de wet van Coulomb als een vector is:

 Deze vorm van de Coulomb -wet is alleen van toepassing op specifieke belastingen.

Toepassing van de Coulomb -wet 

Coulomb gebruikte een apparaat met de naam Torsiebalans Voor uw experimenten. Hierdoor kan de waarde van de elektrostatische constante worden vastgesteld in:

k_En = 8.99 x 10⁹ N m²/C² ≈ 9.0 x 10⁹ N m²/C²

Vervolgens zullen we een applicatie zien. Je hebt drie specifieke belastingen die_NAAR, Q_B en Q_C gevonden in de posities aangegeven in figuur 2. Laten we de netto kracht op q berekenen_B.

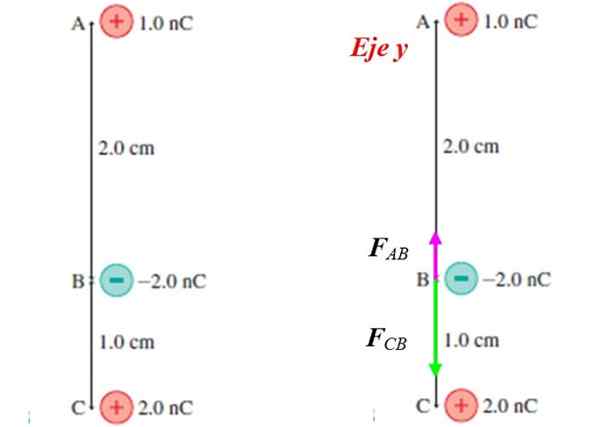Figuur 2. De kracht op de negatieve belasting wordt berekend door de wet van Coulomb. Bron: f. Zapata.

De lading q_NAAR trekt de belasting aan Q aan_B, Omdat het tegengestelde tekenen zijn. Hetzelfde kan gezegd worden over Q_C. Het geïsoleerde lichaamsdiagram bevindt zich in figuur 2 aan de rechterkant, waaruit blijkt dat beide krachten worden gericht langs de verticale as of y -as en tegengestelde zintuigen hebben.

De netto kracht op de belasting q_B is:

F_R = F_Aab + F_CB (Superposition Principle)

Het blijft alleen om numerieke waarden te vervangen, en zorg ervoor dat alle eenheden in het International System (SI) worden geschreven.

F_Aab = 9.0 x 10⁹ x 1 x 10^-9 x 2 x 10^-9 / (2 x 10^-2)) ² N (+En) = 0.000045 (+En) N

F_CB = 9.0 x 10⁹ x 2 x 10^-9 x 2 x 10^-9 / (1 x 10^-2)) ² N (-En) = 0.00036 (-En) N

F_R = F_Aab + F_CB = 0.000045 (+En) + 0.00036 (-En) N = 0.000315 (-En) N

Zwaartekracht en elektriciteit

Deze twee krachten hebben dezelfde wiskundige vorm. Natuurlijk verschillen ze in de waarde van de evenredigheidsconstante en waarin zwaartekracht werkt met massa's, terwijl elektriciteit het doet met belastingen.

Kan u van dienst zijn: dynamiek van een deeltjessysteem: voorbeelden, oefeningen

Maar het belangrijkste is dat beide afhankelijk zijn van het omgekeerde van het kwadraat van de afstand.

Er is een uniek type massa en wordt als positief beschouwd, dus de zwaartekracht trekt altijd aan, terwijl ladingen positief of negatief kunnen zijn. Daarom kunnen elektrische krachten aantrekkingskracht of afstoting zijn, zoals het geval.

En we hebben dit detail dat voortkomt uit het bovenstaande: alle objecten in vrije val hebben dezelfde versnelling, terwijl ze in de buurt van het aardoppervlak zijn.

Maar als we een proton en een elektron in de buurt van een geladen vlak loslaten, zal het elektron bijvoorbeeld een veel grotere versnelling hebben dan dat van het proton. Bovendien zullen versnellingen tegengestelde zintuigen hebben.

Ten slotte wordt de elektrische lading gekwantiseerd, zoals vermeld. Dat betekent dat we ladingen 2,3 of 4 keer kunnen vinden die van het elektron -of dat van het proton -maar nooit 1.5 keer deze belasting. De massa zijn in plaats daarvan geen veelvouden van een unieke massa.

In de wereld van subatomaire deeltjes overschrijdt de elektrische kracht de zwaartekrachtgrootte. Op macroscopische schalen is de zwaartekracht echter degene die overheerst. Waar? Op het niveau van de planeten, het zonnestelsel, van de melkweg en meer.

Referenties

1. Figueroa, D. (2005). Serie: Physics for Science and Engineering. Deel 5. Elektrostatica. Uitgegeven door Douglas Figueroa (USB).
2. Giancoli, D. 2006. Fysica: principes met toepassingen. 6e. Ed Prentice Hall.
3. Kirkpatrick, l. 2007. Natuurkunde: een blik op de wereld. 6e afgekort editie. Cengage leren.
4. Ridder, r. 2017. Fysica voor wetenschappers en engineering: een strategiebenadering. Pearson.
5. Sears, Zemansky. 2016. Universitaire natuurkunde met moderne natuurkunde. 14e. ED. V 2.