Axiale belasting hoe berekend en opgeloste oefeningen

De Axiale belasting Het is de kracht die parallel is gericht aan de symmetrieas van een element dat een structuur vormt. Axiale kracht of belasting kan spanning of compressie zijn. Als de werklijn van de axiale kracht samenvalt met de symmetrieas die door het zwaartepunt van het beschouwde element gaat, wordt gezegd dat het een concentrische axiale belasting of kracht is.

Integendeel, als het een axiale kracht of belasting is parallel aan de symmetrieas, maar wiens werklijn niet op de as zelf staat, is het een excentrieke axiale kracht.

Figuur 1. Axiale belasting. Bron: zelf gemaakt

In figuur 1 vertegenwoordigen gele pijlen krachten of axiale belastingen. In het ene geval is het een concentrische spanningskracht en in de andere worden we geconfronteerd met een excentrieke compressiekracht.

De maateenheid van de axiale belasting in het internationale systeem als het de Newton (N) is. Maar andere krachteenheden zoals kilogram-force (kg-F) en pond sterkte (LB-F) worden vaak gebruikt (LB-F).

[TOC]

Hoe wordt het berekend?

Om de waarde van de axiale belasting in de elementen van een structuur te berekenen, moeten de volgende stappen worden gevolgd:

- Maak het krachtdiagram op elk element.

- Pas de vergelijkingen toe die het translationele evenwicht garanderen, dat wil zeggen dat de som van alle krachten nietig is.

- Overweeg de vergelijking van knooppunten of momenten zodat de rotatiebalans is vervuld. In dit geval moet de som van alle knooppunten nietig zijn.

- Bereken de krachten, en identificeer axiale krachten of belastingen in elk van de elementen.

Axiale belastingrelatie met normale inspanning

De gemiddelde normale inspanning wordt gedefinieerd als het quotiënt tussen de axiale belasting verdeeld tussen de dwarsdoorsnede van het gebied. De eenheden van normale inspanningen in het internationale systeem.Je. Ze zijn Newton op vierkante meter (N/ m²) of Pascal (PA). Figuur 2 illustreert het concept van normale inspanningen voor duidelijkheid.

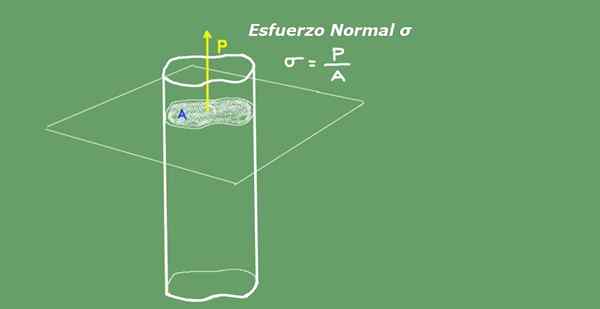Figuur 2. Normale inspanning. Bron: zelf gemaakt.

Opgeloste oefeningen

-Oefening 1

Overweeg een cilindrische betonnen kolom H en radio R. Neem aan dat de dichtheid van beton ρ is. De kolom ondersteunt geen extra belasting dan zijn eigen gewicht en wordt ondersteund op een rechthoekige basis.

- Zoek de waarde van de axiale belasting op punten A, B, C en D, die zich in de volgende posities bevinden: A aan de basis van de kolom, B A ⅓ van de hoogte H, C A ⅔ van de hoogte H en eindelijk D aan de bovenkant van de kolom.

- Bepaal ook de gemiddelde normale inspanning in elk van deze posities. Neem de volgende numerieke waarden: h = 3m, r = 20 cm en ρ = 2250 kg/m³

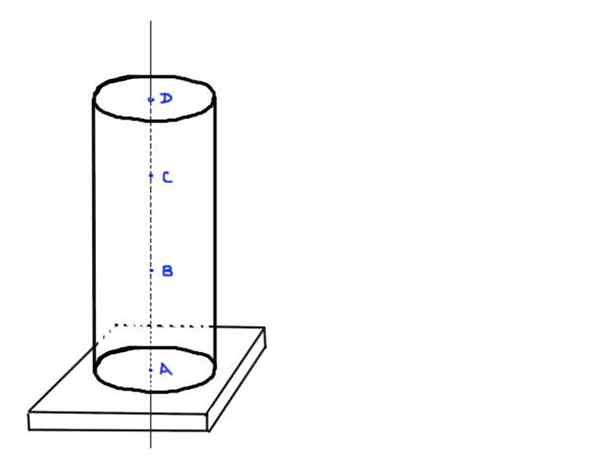figuur 3. Cilindrische kolom. Bron: zelf gemaakt.

Oplossing

Totale kolomgewicht

Het totale gewicht W van de kolom is het product van zijn dichtheid door het volume vermenigvuldigd met de versnelling van de zwaartekracht:

W = ρ ∙ h ∙ π ∙ r² ∙ g = 8313 n

Axiale belasting in een

Op het punt naar de kolom moet het zijn gehele gewicht ondersteunen, zodat de axiale belasting op dit punt is compressie gelijk is aan het gewicht van de kolom:

Pa = w = 8313 n

Axiale belasting in B

Op punt B zal alleen zijn ⅔ van de kolom, dus de axiale belasting op dat punt zal compressie zijn en de ⅔ waarde van het gewicht van de kolom:

Pb = ⅔ w = 5542 n

figuur 3. Cilindrische kolom. Bron: zelf gemaakt.

Boven positie C zijn er alleen kolom ⅓, dus de axiale compressiebelasting zal ⅓ van zijn eigen gewicht zijn:

Pc = ⅓ w = 2771 n

Axiale belasting in D

Eindelijk op punt D dat het bovenste uiteinde van de kolom is, is er geen belasting, dus de axiale kracht op dat punt is nietig.

Pd = 0 n

Normale inspanningen in elk van de posities

Om de normale inspanning in elk van de posities te bepalen, is het nodig om de dwarsdoorsnede van gebied A te berekenen, die wordt gegeven door:

A = π ∙ r² = 0.126m²

Op deze manier zal de normale inspanning in elk van de posities het quotiënt zijn tussen de axiale kracht in elk van de punten verdeeld tussen de al berekende doorsnede, die in deze oefening voor alle punten hetzelfde is omdat het een kolomcilindrisch is.

σ = p/a; σa = 66,15 kPa; σb = 44.10 kPa; σc = 22,05 kPa; σd = 0,00 kPa

-Oefening 2

De figuur toont een structuur die bestaat uit twee staven die we AB en CB zullen noemen. De AB -balk wordt aan het einde A met de ene door een pin ondersteund en aan het andere uiteinde verbonden met de andere balk via een andere b -pin.

Evenzo wordt de CB -balk aan het einde C ondersteund door middel van een pin en aan het einde B met pin B die deze verenigt naar de andere balk. Een verticale kracht of belasting F wordt toegepast op pennen B zoals getoond als de volgende figuur laat zien:

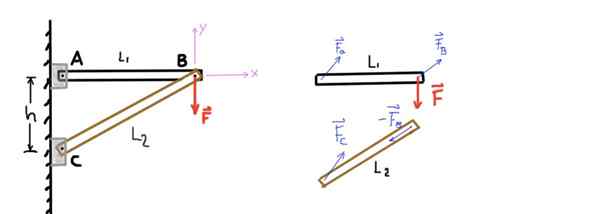Figuur 4. Twee bars structuur en vrij lichaamsdiagram. Bron: zelf gemaakt.

Ga uit van het gewicht van de verachtelijke balken, omdat de kracht F = 500 kg-F veel groter is dan het gewicht van de structuur. De scheiding tussen ondersteuning A en C is h = 1,5 m en de lengte van de AB -balk is L1 = 2 m. Bepaal de axiale belasting in elk van de staven, wat aangeeft of het axiale compressie of spanningsbelasting is.

Oplossing 2

De figuur toont, door een vrij lichaamsdiagram, de krachten die op elk van de elementen van de structuur werken. Het Cartesiaanse coördinatensysteem wordt ook aangegeven waarmee de evenwichtsvergelijkingen van krachten zullen worden verhoogd.

De knooppunten of momenten worden berekend op punt B en worden als positief beschouwd als ze uit het scherm wijzen (Z -as). De balans van krachten en knooppunten voor elke balk is:

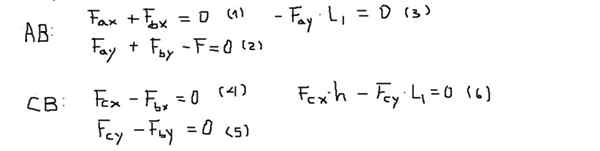
Vervolgens zijn de componenten van de krachten van elk van de vergelijkingen duidelijk na de volgende volgorde:

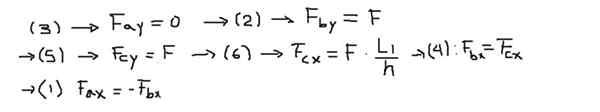
Ten slotte worden de resulterende krachten berekend aan de uiteinden van elke balk:

Opgemerkt kan worden dat de krachten aan de uiteinden van elk van de staven parallel aan hen zijn, wat bevestigt dat het axiale krachten of belastingen zijn. In het geval van de AB -balk is het een axiale spanningskracht waarvan de waarde is:

F ∙ (L1/H) = 500 kg-F ∙ (2,0 m/1,5 m) = 666,6 kg-F = 6533.3 n

De CB Bar is in compressie vanwege de twee krachten die aan hun uiteinden werken die evenwijdig zijn aan de bar en naar hun centrum wijzen. De grootte van de axiale compressiekracht in de CB -balk is:

F ∙ (1 + l1²/h²) 1/2 = 500 kg-f ∙ (1 + (2/1.5) ²) 1/2 = 833,3 kg-f = 8166.6 n

Referenties

1. Bier f ... materiële mechanica. 5e. Editie. 2010. MC Graw Hill. 1-130.
2. Hibbeler R. Materiaalmechanica. Achtste editie. Prentice Hall. 2011. 3-60.
3. Gere J. Materiaalmechanica. Achtste editie. Cengage leren. 4-220.
4. Giancoli, D. 2006. Fysica: principes met toepassingen. 6e ed. Prentice Hall. 238-242.
5. Valera Negrete, J. 2005. ALGEMENE FYSICA -NOTIES. UNAM. 87-98.