Golfkenmerken

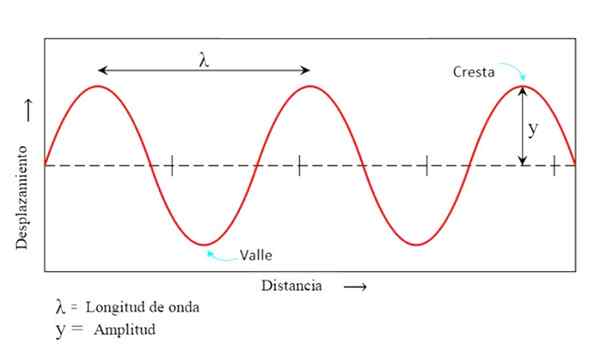
Figuur 1. Representatieve parameters van een sinusvormige golf. Bron: f. Zapata.

De Golfkenmerken Ze zijn het onderscheidende van het golvende fenomeen: de golflengte, de frequentie, de valleien, de richels, de snelheid, de energie en anderen die we in dit artikel zullen verklaren.

In golven zijn het geen deeltjes die reizen met verstoring, maar energie. Wanneer een golf zich verspreidt in een materiaalmedium, dat onder andere water, lucht of een touw kan zijn, bewegen de deeltjes gewoon van de evenwichtspositie, om er na een korte tijd naar terug te keren.

De beweging wordt echter van het ene deeltje naar het andere overgedragen, waardoor elk van hen trilt. Op deze manier verspreidt de verstoring die we noemen zich in het midden verspreiden stemming, Zoals de golf van fans in de stadions doet, wanneer voetbalwedstrijden worden gespeeld.

De studie van golven is erg interessant, omdat we in een wereld vol van hen leven: licht, zeegolven, het geluid van muziek en stem zijn allemaal golvende fenomenen, hoewel van verschillende aard. Zowel licht als geluid zijn bijzonder belangrijk, omdat we ze voortdurend nodig hebben om met de buitenwereld te communiceren.

Wat zijn de kenmerken van de golven?

Trilling

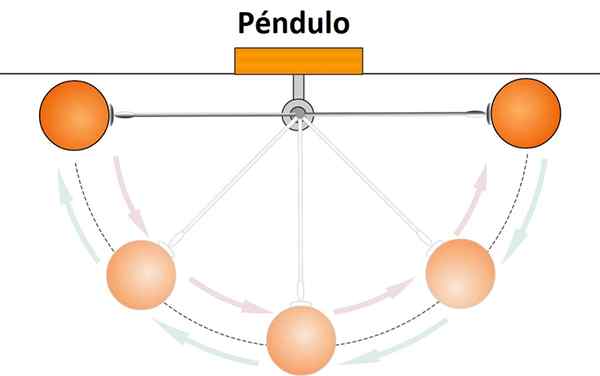
Het is de complete tour die een deeltje maakt in zijn swingende beweging. Een slinger heeft bijvoorbeeld een beweging van swing, omdat het vanaf een bepaald punt een boog beschrijft, stopt wanneer deze een bepaalde hoogte bereikt en terugkeert naar zijn oorspronkelijke positie.

Als het niet voor wrijving was geweest, zou deze beweging voor onbepaalde tijd volgen. Maar vanwege wrijving wordt de beweging langzamer en langzamer en de minst brede oscillatie, totdat de slinger stopt.

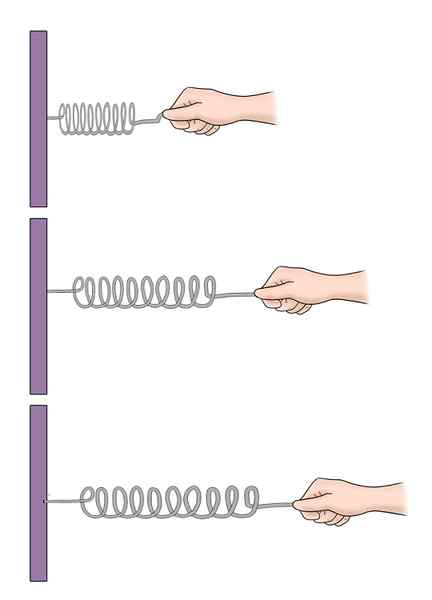
Het kan u van dienst zijn: tweede wet van thermodynamica: formules, vergelijkingen, voorbeelden

Wanneer een horizontaal gespannen touw wordt verstoord, trillen de deeltjes van het touw in een verticale richting, dat wil zeggen van boven naar beneden, terwijl de verstoring horizontaal langs het touw reist.

Oscillatiecentrum

Wanneer een deeltje zijn slingerende beweging maakt, maakt het het beweegt ten opzichte van een bepaald punt, genaamd Origin of Oscillation Center.

In het voorbeeld van de slinger is het op het laagste punt in evenwicht en oscilleert hier rond als we het een beetje van deze positie scheiden. Daarom kan dit punt worden beschouwd als het centrum van de oscillatie.

We kunnen ons ook een veer of veer voorstellen op een horizontale tafel, onderhevig aan het ene uiteinde aan een muur, en met een blok aan de andere kant. Als het Spring-brush-systeem niet in de buurt is, bevindt het blok zich in een bepaalde evenwichtspositie.

Bij het een beetje comprimeren of strekken van de veer begint het systeem te oscilleren rond die evenwichtspositie.

Verlenging

Het is de afstand die het deeltje na een tijdje weggaat van het oscillatiecentrum. Het wordt gemeten in meters wanneer het internationale systeem wordt gebruikt als.

Als een veer wordt gecomprimeerd of uitgerekt met een blok aan de ene kant, wordt gezegd dat het een verlenging van het "X" aantal meters, centimeters of de eenheid heeft ervaren die wordt gebruikt om de afstand te meten.

Richels en valleien

Ze zijn respectievelijk de hoogste en laagste punten die het deeltje bereikt ten opzichte van de evenwichtspositie y = 0 (zie figuur 1).

Amplitude

De golven van de zee, wanneer ze veel amplitude hebben, dragen veel energie

Het is de maximale afstand die het deeltje scheidt van het oscillatiecentrum en ook in meters wordt gegeven. Het wordt aangeduid als NAAR of als En. Daar valt de evenwichtspositie samen met y = 0 en komt overeen met de ribbels en golfvalleien.

Kan u van dienst zijn: dynamische of kinetische wrijving: coëfficiënt, voorbeelden, oefeningen

De amplitude is een belangrijke parameter, omdat deze gerelateerd is aan de energie die de golf transporteert. Hoe groter de amplitude, hoe groter de energie, zoals bij de golven van de zee, bijvoorbeeld.

Knooppunt

De knooppunten zijn de punten waarop het deeltje door het oscillatiecentrum of evenwichtspositie gaat.

Fiets

Dit wordt een complete oscillatie genoemd, wanneer het deeltje van de ene top naar de volgende gaat, of van een vallei naar de volgende. Dan zeggen we dat hij een cyclus heeft gemaakt.

De slinger voert een volledige oscillatie uit wanneer een bepaalde hoogte van de evenwichtspositie wordt verplaatst, door het laagste punt gaat, stijgt naar dezelfde hoogte op een reis en keert terug naar de eerste hoogte in retourtrip.

Periode

Omdat de golven repetitief zijn, is de deeltjesbeweging krant. De periode is de tijd die nodig is om een ​​volledige oscillatie te maken en wordt meestal geweigerd met de Letter T hoofdletters. De eenheden van de periode in het internationale systeem als ze de tweede zijn.

Frequentie

Het is de omgekeerde of wederzijdse grootte van de periode en is gerelateerd aan de hoeveelheid oscillaties of cycli die per tijdseenheid is gemaakt. Het wordt aangeduid met de brief F.

Aangezien de hoeveelheid oscillaties geen eenheid is, worden de seconden voor de frequentie gebruikt^-1 (S^-1), Hertz of Hertzios genoemd en afgekort Hz.

Omdat we het omgekeerde van de periode zijn, kunnen we een wiskundige relatie tussen beide magnitudes schrijven:

F = 1 /t

O goed:

T = 1/f

Als bijvoorbeeld een slinger 30 cycli in 6 seconden uitvoert, is de frequentie ervan:

F = (30 cycli)/(6 s) = 5 cycli/s = 5 Hz.

Kan u van dienst zijn: Relatieve dichtheid: berekening, voorbeelden, oefeningen

Golflengte

Het is de afstand tussen twee punten van een golf die op dezelfde hoogte is, op voorwaarde dat een volledige oscillatie is uitgevoerd. Het kan worden gemeten van de ene top naar de andere opeenvolgende opeenvolgende.

De golflengte wordt aangegeven door de Griekse letter λ, die "lambda" leest en wordt gemeten in afstandseenheden zoals de meters van het internationale systeem, hoewel er zo'n grote verscheidenheid aan golflengten is, dat de veelvouden en ondermultaten frequent zijn.

Golfnummer

Het is de omgekeerde grootte van de golflengte, vermenigvuldigd met nummer 2π. Daarom hebben we door het golfnummer aan te geven met letter K:

K = 2π / λ

Propagatiesnelheid

Het is de snelheid waarmee de verstoring reist. Als het medium waarin de golf zich voortplant, homogeen en isotropisch is, dat wil zeggen, de eigenschappen zijn overal hetzelfde, dan is deze snelheid constant en wordt gegeven door:

V = λ / t

De eenheden van de voortplantingssnelheid zijn dezelfde als die van een andere snelheid. In het internationale systeem komt overeen met M/S.

Aangezien de periode het omgekeerde van de frequentie is, kan deze ook worden uitgedrukt:

v = λ . F

En omdat de snelheid constant is, het product λ.F ook, zodat als bijvoorbeeld de golflengte wordt gewijzigd, de frequentie verandert zodat het product hetzelfde blijft.

Referenties

1. Giancoli, D.  2006. Fysica: principes met toepassingen. 6e. Ed Prentice Hall.
2. Hewitt, Paul. 2012. Conceptuele fysieke wetenschap. 5e. ED. Pearson.
3. Sears, Zemansky. 2016. Universitaire natuurkunde met moderne natuurkunde. 14e. ED. Deel 1. Pearson.
4. Serway, r., Jewett, J. (2008). Natuurkunde voor wetenschap en engineering. Deel 1. 7e. ED. Cengage leren.
5. Tipler, p. (2006) Natuurkunde voor wetenschap en technologie. 5e ed. Deel 1. Redactioneel teruggekeerd.