elektrisch veld

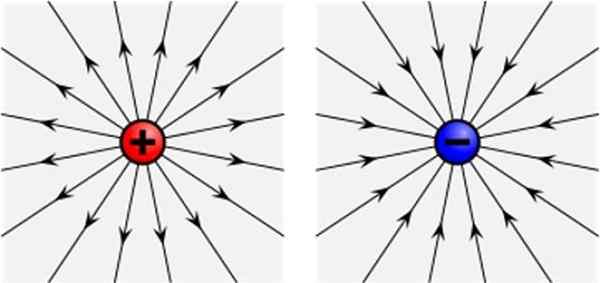
Het elektrische veld van een positieve (links) en negatieve (rechts). Bron: Wikimedia Commons

Wat is het elektrische veld?

Hij elektrisch veld Het is de eigenschap die de objecten geladen hebben met het beïnvloeden van de omliggende ruimte, die wordt waargenomen door andere elektrisch geladen lichamen. Maar in tegenstelling tot de elektrische kracht tussen belastingen, hangt het elektrische veld alleen af ​​van de belasting die het produceert.

Michael Faraday (1791-1867), een Engelse natuurkundige, creëerde het concept van veld door op te merken dat elke elektrische lading de ruimte beïnvloedt, zodat het niet in contact hoeft te zijn met een andere belasting zodat de interactie optreedt.

Het is zelfs niet nodig dat de belastingen zich in een materiaalmedium bevinden, omdat de interactie in een vacuüm kan worden gegeven.

Om de vorm van een elektrisch veld te visualiseren, stel dat een specifieke en positieve belasting, +Q wordt genoemd, waarvan de grootte zo klein is dat het niet nodig is om rekening te houden met de afmetingen. Het veld dat ze produceert, is in staat om andere ladingen te beïnvloeden, zoals een andere positieve testpuntbelasting q_of.

De testbelasting wordt op verschillende locaties rond +Q geplaatst, en voor beide positief, de kracht die +Q uitgeeft op Q_of Het is afstoting.

De krachtkracht tekenen op de belasting q_of Op elk punt van de ruimte die het inneemt, en het verwijdert, is er een set lijnen die radiaal uit de load +q tevoorschijn komen (zie de afbeelding hierboven, links).

Bij het herhalen van de ervaring met een negatieve belasting - q, zijn de lijnen ook radiaal, maar komen naar - q. In beide gevallen zijn de lijnen rangent naar het vector elektrische veld van de belasting, het extra in de omgang wanneer het positief is en inkomend als het negatief is.

Formule en eenheden

Als er in een ruimte met ruimte een elektrisch veld is EN, Een elektrische lading Q_of Ervaring, dankzij hem, een kracht gegeven door:

Kan u van dienst zijn: Willekeurige fout: formule en vergelijkingen, berekening, voorbeelden, oefeningen

F = q_ofEN

Zodat:

De elektrische veldeenheid in het internationale systeem van eenheden is Newton/Coulomb, dat is afgekort N/C. Het is ook gebruikelijk om het elektrische veld uit te drukken in termen van een scalaire grootte die elektrische potentiaal wordt genoemd, in welk geval het veld voor het veld de volt/meter (v/m) is.

Het elektrische veld van een punctuele belasting

Veld EN wordt geproduceerd door een object met belasting Q. De proefbelasting erg klein maken, dat wil zeggen, Q maken_of neig naar 0, de vector EN is:

Met F_of De kracht tussen Q en Q_of.

De intentie bij het nemen van de limiet is om de proefbelasting klein genoeg te maken, zodat het veld niet verandert die wil berekenen.

Als wat een punctuele last is, volgens de wet van Coulomb, de kracht tussen de aanklachten Q en Q_of, Beide gescheiden een afstand R, wordt gegeven door:

In deze vergelijking is k de elektrostatische constante en de eenheidsvector in de richting van de lijn die Q en Q en Q verenigt_of is:

Deze uitdrukking vervangt in de definitie van het veld, deze wordt verkregen:

 Zodat het veld EN, Geproduceerd door de punctuele belasting Q op punt P, is:

Dus, EN Het hangt niet af van de proefbelasting, maar van de belasting die het produceert. De grootte van het veld is recht evenredig met de grootte van de belasting en omgekeerd evenredig met het kwadraat van de afstand tussen de belasting en het punt P.

En zoals in het begin vermeld, de adres Vanuit het veld is het radiaal en de richting is extravert naar de belasting wanneer deze positief is en inkomend wanneer het negatief is.

Elektrische veldintensiteit

Het elektrische veld is vector en de intensiteit verwijst naar zijn module of grootte, die zonder vet wordt aangeduid. Voor een punctuele belasting is de intensiteit van zijn elektrische veld eenvoudig:

Kan u van dienst zijn: oppervlakkige verwijding: formule, coëfficiënten en voorbeelden

 En omdat het de module van een hoeveelheid is, is het altijd positief.

De intensiteit van het elektrische veld geproduceerd door een belasting q = - 4.3 μC (μC luidt "Microcoulomb" en is gelijk aan de miljoenste van een Coulomb), op een afstand van 2 cm van de belasting, het is:

Merk op dat de afstand van 2 cm meters werd, vermenigvuldigd door de kracht 10⁻², Omdat de elektrostatische constante zich in eenheden bevindt als. En hoewel de belasting negatief is, is de intensiteit van het veld dat het produceert altijd positief, maar de elektrische veldvector is inkomend aan de belasting, zoals eerder uitgelegd.

Voorbeelden van elektrische veld

1. Elektrisch veld van een discrete verdeling van belastingen

Een reeks specifieke kosten wordt genoemd Discrete laadverdeling. In dat geval wordt het resulterende elektrische veld op punt P berekend door het toepassen van de Superpositieprincipe, dat is de somvector van het veld dat elk van de ladingen produceert in P:

EN_netto = EN₁ + EN₂ + EN₃ +..

De volgende afbeelding toont een verdeling bestaande uit vijf specifieke belastingen en het elektrische veld dat elk produceert op punt P:

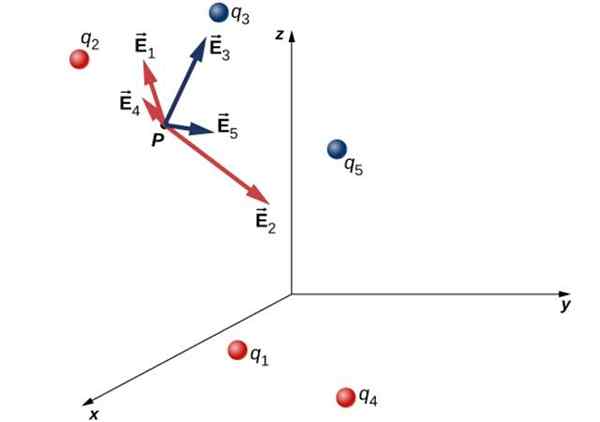Elektrisch veld op punt P, vanwege een discrete verdeling van belastingen

• De ladingen q₃ en Q₅ Ze zijn negatief en het veld dat ze produceren is inkomend voor hen. Ze worden in het blauw onderscheiden.
• Van zijn kant, de ladingen q₁, Q₂ en Q₄ Ze zijn positief en creëren een opvallend veld in rood.

2. Elektrisch veld van een continue verdeling van belastingen

Een continue belastingsverdeling bestaat uit een uitgebreid object, elektrisch geladen, zoals die getoond in de volgende figuur. Aangezien het object aanzienlijke dimensies heeft, is het veld dat een deel van het lichaam in P produceert aanzienlijk anders dan het lichaam dat nog een andere (of dichtstbijzijnde) van P produceert.

Kan u van dienst zijn: Kirchhoff -wetten

Stel dat een kleine elektrische lading van dit object wordt genomen, DQ genoemd en verondersteld positief, die in P een kleine bijdrage produceert aan het totale elektrische veld. Deze bijdrage is een verschil van de elektrische veldvector dEN.

Omdat de DQ -belasting erg klein is, is het veld als dat van een punctuele belasting, dus de vergelijking kan worden toegepast voordat het wordt gezien:

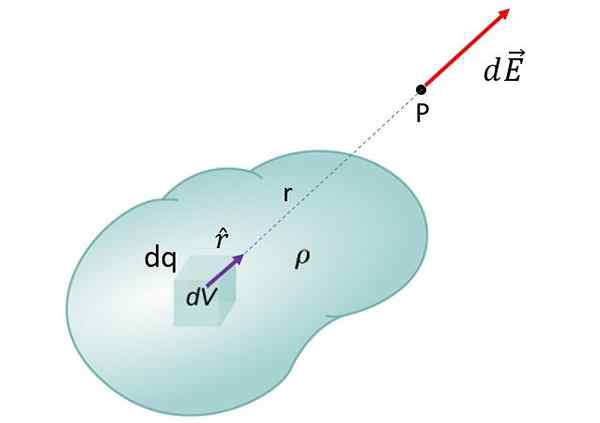Om het elektrische veld van een uitgebreid object te berekenen, is het boven al zijn volume geïntegreerd. De belastingsdichtheid (belasting per volume -eenheid) wordt aangeduid als ρ

Om het totale veld van het object op punt P te verkrijgen, worden de bijdragen van alle DQ die op het object kunnen worden genomen, toegevoegd. Dit leidt tot de integraal:

Oefening opgelost

Een punctuele belasting q = 2.0 × 10⁻⁸ C wordt op een punt P geplaatst in een elektrisch veld, waarin het een stijgende kracht van grootte 4 ervaart 4.0 × 10⁻⁶ N. Berekenen:

a) het elektrische veld in p

b) De kracht op een belasting q = −1.0 × 10⁻⁸ C gelegen in P.

Oplossing voor

Wees de grootte van het elektrische veld waarin de belasting wordt geplaatst. Op grond van dit veld ervaart deze belasting de opwaartse kracht van grootte F, zodat:

F = q ∙ e

Dus:

E = f /q = 4.0 × 10^-6 N/ 2.0 × 10^-8 C = 200 N/C.

Positief zijn De last, kracht en veld hebben dezelfde richting en betekenis.

Oplossing B

De omvang van de kracht die werkt op wat is:

Wanneer deze last negatief is, hebben kracht en veld dezelfde richting, maar tegengestelde zintuigen.

Referenties

1. Bauer, W. 2011. Fysica voor engineering en wetenschappen. Deel 2. MC Graw Hill. 
2. Veld en elektrische potentiaal van een punctuele belasting. Opgehaald uit: SC.Ehu.is.
3. Resnick, r. (1999). Fysiek. Vol. 1. 3e ed. in het Spaans. Continental Editorial Company s.NAAR. van C.V.
4. Sears, Z. (2016). Universitaire natuurkunde met moderne natuurkunde. 14e. ED. Deel 1. Pearson.
5. Universiteitsfysica. Elektrisch veld. Vol. 2. Opgehaald uit: OpenStax.borg.