Randen van een kubus

Wat is de rand van een kubus?

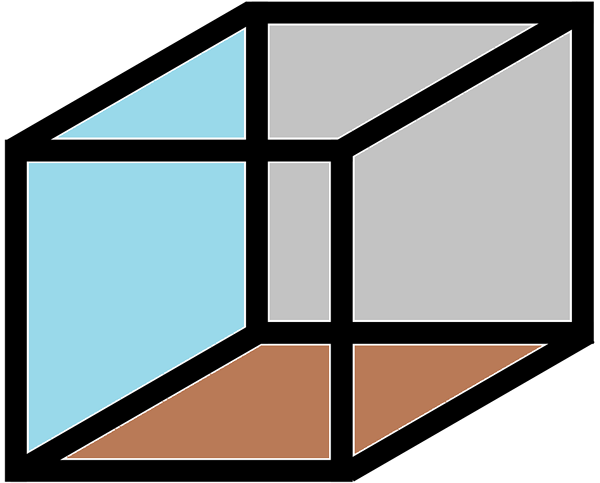
De rand van een kubus Het is een rand ervan: het is de lijn die samenkomt met twee hoekpunten of hoeken. Een rand is de lijn waar twee zijden van een geometrische figuur worden onderschept. Een kubus heeft 12 randen.

De vorige definitie is algemeen en is van toepassing op een geometrische figuur, niet alleen voor de kubus. Als het gaat om een ​​vlakke figuur, komen de randen overeen met de zijkanten van genoemde figuur.

Het wordt parallellepiped genoemd met een geometrische figuur met zes gezichten in de vorm van parallellogrammen, waarvan de tegenstellingen gelijk en parallel aan elkaar zijn.

In het specifieke geval waarin de gezichten vierkant zijn, wordt de parallellepiped een kubus of hexaedro genoemd, een figuur die wordt beschouwd als een reguliere polyhedron.

Manieren om de randen van een kubus te identificeren

Voor een betere illustratie kunnen alledaagse objecten worden gebruikt om nauwkeurig te bepalen welke de randen van een kubus zijn.

1- Armando een papieren kubus

Als u kunt zien hoe een papieren of kartonnen emmer is gebouwd, kunt u zien wat uw randen zijn. Het begint een kruis te trekken zoals de figuur en bepaalde lijnen binnen zijn gemarkeerd.

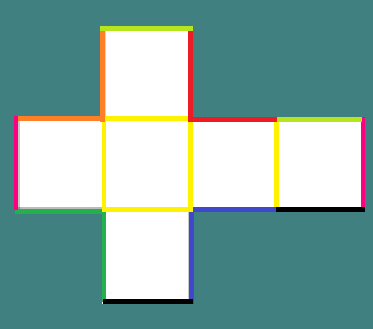
Elk van de gele lijnen vertegenwoordigt een vouw, die een rand van de kubus (rand) zal zijn.

Evenzo zal elk paar lijnen met dezelfde kleur een voorsprong vormen wanneer ze zich aansluiten. In totaal heeft een kubus 12 randen.

2- Een kubus tekenen

Een andere manier om te zien wat de randen van een kubus zijn, is om te observeren hoe het wordt getekend. Je begint met het tekenen van een vierkant van zij L; Elke kant van het vierkant is een rand van de kubus.

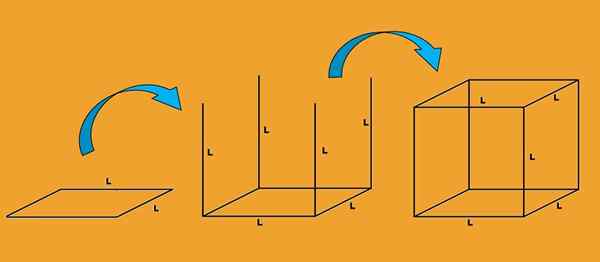
Vervolgens worden vier verticale lijnen uit elk hoekpunt getrokken, en de lengte van elk van deze lijnen is L. Elke lijn is ook een emmerrand.

Ten slotte wordt nog een vierkant L getekend, zodat de hoekpunten samenvallen met het einde van de randen die in de vorige stap zijn getekend. Elk van de zijkanten van dit nieuwe vierkant is een rand van de kubus.

3- Rubik-kubus

Om de geometrische definitie te illustreren die zich in het begin heeft voorgedaan, kunt u een Rubik -kubus zien.

Elk gezicht heeft een andere kleur. De randen worden weergegeven door de lijn waar gezichten worden onderschept met verschillende kleuren.

Euler Stelling

De stelling van Euler voor polyhedros zegt dat, gezien een polyhedron, het aantal gezichten C plus het aantal hoekpunten V gelijk is aan het aantal randen aan plus 2. Dat wil zeggen, c+v = a+2.

In de vorige afbeeldingen is te zien dat een kubus 6 gezichten, 8 hoekpunten en 12 randen heeft. Daarom vervult het de Euler -stelling voor polyhedra, sinds 6+8 = 12+2.

Het is erg handig om de lengte van een rand van een kubus te kennen. Als de lengte van een rand bekend is, is de lengte van al zijn randen bekend, die bepaalde kubusgegevens kunnen verkrijgen, zoals het volume.

Het volume van een kubus wordt gedefinieerd als l³, waarbij l de lengte van de randen is. Om het volume van de kubus te kennen, is het daarom alleen nodig om de waarde van L te kennen.