Boog (geometrie) maat, soorten bogen, voorbeelden

Hij boog, In geometrie is het elke gebogen lijn die twee punten verbindt. Een gebogen lijn, in tegenstelling tot een rechte lijn, is dat wiens richting anders is op elk punt van hetzelfde. Het tegenovergestelde van een boog is een segment, omdat dit een rechte sectie is die zich bij twee punten verbindt.

De boog die het meest wordt gebruikt in de geometrie is de omtrekboog. Andere bogen van gemeenschappelijk gebruik zijn de parabolische boog, elliptische boog en de vloeiende boog. De boogvorm wordt ook vaak gebruikt in de architectuur als een decoratief element en structureel element. Dit is het geval van de lateien van de deuren en ramen, evenals van de bruggen en aquaducten.

Figuur 1. De regenboog is een gebogen lijn die twee punten aan de horizon verbindt. Bron: Pixabay

[TOC]

De boog en zijn maatregel

De maat van een boog is de lengte, die afhangt van het type curve dat de twee punten en de locatie ervan verbindt.

De lengte van een cirkelvormige boog is een van de gemakkelijkste te berekenen te berekenen, omdat de volledige booglengte of omtrek van een cirkel bekend is.

De omtrek van een cirkel is twee pi keer je radio: P = 2 π r. Dit weten, als u de lengte wilt berekenen S van een cirkelvormige boog van hoek α (gemeten in radianen) en radio R, Er wordt een aandeel toegepast:

(s / p) = (α / 2 π)

Dan opruimen S van de vorige uitdrukking en het vervangen van de omtrek P door zijn uitdrukking afhankelijk van de radio R, Je hebt:

S = (α / 2 π) p = (α / 2 π) (2 π r) = α r.

Dat wil zeggen, de maat van een cirkelvormige boog is het product van zijn hoekopening door de cirkelvormige boogradius.

Voor een boog op een algemene manier is het probleem ingewikkelder, tot het punt dat de grote denkers van de oudheid beweerden dat het een onmogelijke taak was.

Het kan u van dienst zijn: wat zijn algebraïsche uitdrukkingen en welke zijn de meest voorkomende?

Het was pas in de komst van de differentiaal- en integrale calculus in 1665, dat het probleem van de maat voor een boog naar tevredenheid werd opgelost. 

Vóór de uitvinding van de differentiële calculus konden alleen oplossingen worden gevonden door het gebruik van polygonale lijn- of omtrekbogen die de ware boog benaderden, maar deze oplossingen waren niet exact. 

Soorten bogen

Vanuit het oogpunt van de geometrie worden de bogen geclassificeerd volgens de gebogen lijn die twee punten van het vliegtuig verbindt. Er zijn andere classificaties volgens het architectonische gebruik en de vorm ervan.

Circulaire boog

Wanneer de lijn die twee punten van het vlak verbindt een stuk omtrek van een bepaalde straal is, is er een cirkelvormige boog. Figuur 2 toont een cirkelvormige boog van straal R die punten A en B verbindt.

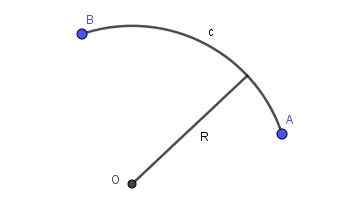Figuur 2. Radio R Circulaire boog die punt A en B verbindt. Bereid door Ricardo Pérez.

Parabolische boog

De gelijkenis is het traject dat volgt op een object dat in schuine vorm in de lucht is gegooid. Wanneer de curve die twee punten verbindt een gelijkenis is, dan is er een parabolische boog zoals die wordt getoond in figuur 3.

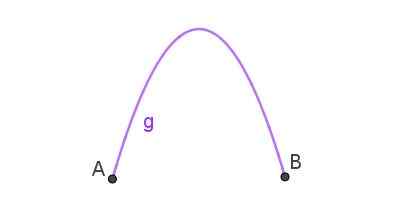figuur 3. Parabolische boog die punten A en B verbindt. Bereid door Ricardo Pérez.

Dit is de vorm die de waterstraal aanneemt die uit een slang komt die wijst. De parabolische boog kan worden waargenomen in de waterbronnen.

Figuur 4. Parabolische boog gevormd door water uit een bron in Dresden. Bron: Pixabay.

Citesair boog

De vloeiende boog is een andere natuurlijke boog. De vloeiender is de curve die van nature wordt gevormd wanneer een ketting of een touw comfortabel hangt van twee afzonderlijke punten.

Kan u van dienst zijn: wat zijn de elementen van een hoek?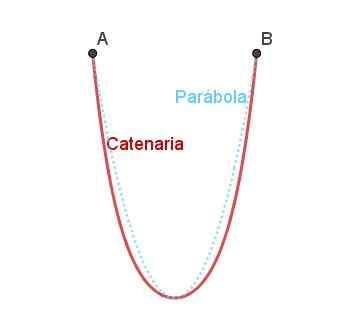 Figuur 5. Cpenary boog en vergelijking met de parabolische boog. Bereid door Ricardo Pérez.

De vloeiendheid is vergelijkbaar met de parabola, maar het is niet precies hetzelfde als het kan worden opgemerkt in figuur 4.

De omgekeerde boogvormige boog wordt in de architectuur gebruikt als een structureel element van hoge compressieresistentie. In feite kan worden aangetoond dat het het meest resistente boogtype is bij alle mogelijke vormen. 

Om een ​​solide boven- en ketting te bouwen, wordt alleen de vorm van een touw of ketting gekopieerd, dan draait de gekopieerde vorm om om deze in de deur lintel of raam te reproduceren.

Elliptische boog

Een boog is elliptisch als de curve die twee punten verbindt een stuk of stuk ellips is. De ellips wordt gedefinieerd als de geometrische plaats van de punten waarvan de afstand tot twee gegeven punten altijd een constante hoeveelheid toevoegt.

De ellips is een curve die in de natuur verschijnt: het is de curve van het traject van de planeet rond de zon, zoals Johannes Kepler demonstreert in 1609.

In de praktijk kan een ellips worden getrokken door twee stutten op de vloer of twee pinnen op papier te zetten en een touw aan hen te binden. Dan is het touw gespannen met de marker of potlood en de curve is getekend. Een stuk ellips is een elliptische boog. De volgende animatie illustreert hoe de ellips wordt getekend:

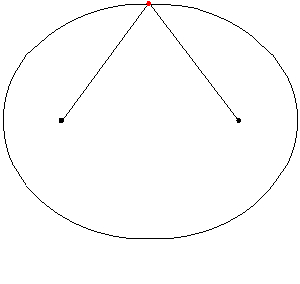Figuur 5. Posen van een ellips met behulp van een gespannen touw. Bron: Wikimedia Commons

Afbeelding 6 toont een elliptische boog die punten g en h verbindt.

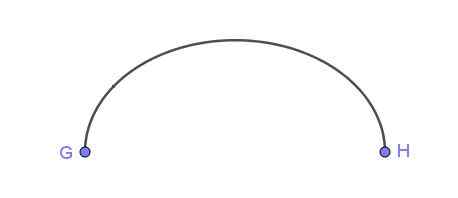Figuur 6. Elliptische boog die twee punten verbindt. Bereid door Ricardo Pérez.

Voorbeelden van bogen

De volgende voorbeelden verwijzen naar hoe de omtrek van sommige specifieke bogen te berekenen.

Kan u van dienst zijn: transcendente nummers: wat zijn, formules, voorbeelden, oefeningen

voorbeeld 1

Figuur 7 toont een venster dat is afgesloten in gesneden cirkelvormige boog. De afmetingen die in de figuur worden getoond, zijn op voeten. Bereken de booglengte.

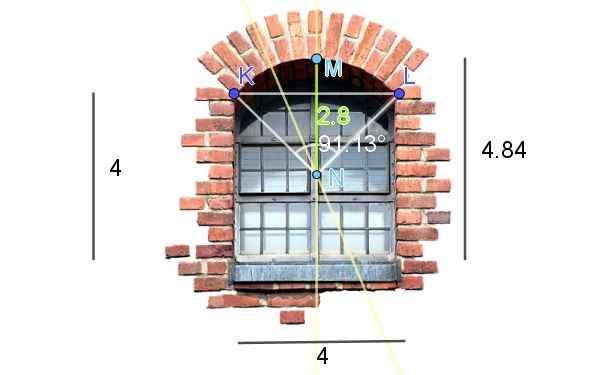Figuur 7. Berekening van de cirkelvormige booglengte van een venster. (Eigen annotaties - Vensterafbeelding in Pixabay)

Om het midden en de straal van de cirkelvormige boog van het latei van het raam te krijgen, worden de volgende constructies op de afbeelding gemaakt:

-Het KL -segment is getekend en de mediatrix is ​​getekend.

-Dan bevindt het hoogste punt van de lintel zich, die we m noemen. Het KM -segment wordt vervolgens overwogen en zijn mediatrix is ​​getekend.

De onderschepping van de twee mediatrices is punt N en is ook het midden van de cirkelvormige boog.

-Nu moet u de lengte van het NM -segment meten, die samenvalt met de straal R van de cirkelvormige boog: r = 2.8 voet.

-Om de lengte van de boog naast de straal te kennen, de hoek die de boog vormt. Die kan worden bepaald door twee methoden, of wordt gemeten met een transporter, of afwisselend berekend met behulp van trigonometrie.

In het getoonde geval is de hoek die de boog vormt 91,13º, die moet worden omgezet in radianen:

 91,13º = 91,13º * π / 180º = 1.59 radialen

We berekenen eindelijk de lengte S van de boog door de formule S = α r.

S = 1,59 * 2.8 voet = 4,45 voet

Voorbeeld 2

Zoek de lengte van de elliptische boog getoond in figuur 8, bekend R en de kleine semi -as S van de ellips.

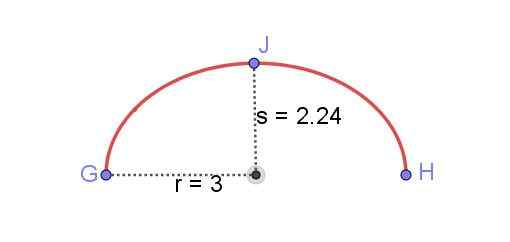Figuur 8. Elliptische boog tussen GH. Bereid door Ricardo Pérez.

Het vinden van de lengte van een ellips was lange tijd een van de moeilijkste problemen van de wiskunde. Oplossingen uitgedrukt door elliptische integralen kunnen worden verkregen, maar om een ​​numerieke waarde te hebben, moeten deze integralen in de power -serie worden uitgebreid. Een exact resultaat zou oneindige termen van die series vereisen.

Gelukkig vond het wiskundige genie van de hindoe -oorsprong Ramanujan, die tussen 1887 en 1920 leefde, een formule die zeer precies de omtrek van een ellips benadert:

Perimeter van een ellips = π [3 (r + s) - √ ((3r + s) (r + 3s))]]]

De perimeter van een ellips met r = 3 cm en s = 2.24 cm is 16,55 cm. De getoonde elliptische boog heeft echter de helft van die waarde:

Elliptische booglengte GH = 8.28 cm.

Referenties

1. Clemens S. 2008. Geometrie en trigonometrie. Pearson Education.
2. Garcia F. Numerieke procedures in Java. Lengte van een ellips. Opgehaald uit: SC.Ehu.is
3. Dynamische geometrie. Bogen. Hersteld van geometriadinamica.is
4. Pizedas. Ellipsen en gelijkenissen om ons heen. Opgehaald uit: pizedas.com
5. Wikipedia. Arc (geometrie). Hersteld van: het is.Wikipedia.com