X Squared

We leggen uit wat X Squared is, de eigenschappen, voorbeelden en oefeningen opgelost

Het gebied van een vierkant van "x" kant is x kwadraat. Bron: f. Zapata.

De algebraïsche werking van "X Squared"Het wordt uitgevoerd door de hoeveelheid" x "twee keer met zichzelf te vermenigvuldigen. Het maakt deel uit van de potentiëringsoperaties en in wiskundige symbolen wordt het op deze manier uitgedrukt:

x ∙ x = x²

Dit is een bepaald geval van empowerment, waarin "x" de baseren En de "2" is de exponent. Als in een bewerking de term X verschijnt², Het leest precies als "X Squared" of "X Square verhoogd".

Natuurlijk zijn andere exponenten mogelijk, bijvoorbeeld als de exponent 3 is, dan wordt de stroom geschreven als:

x ∙ x ∙ x = x³

En lees als "x naar de drie", "x verhoogd naar de kubus" of gewoon "x naar de kubus".

Over het algemeen kan de exponent waaraan de basis hoog is elk getal zijn, "n" genoemd en in dat geval wordt de overeenkomstige kracht geschreven:

X^N = x ∙ x ∙ x ∙… ∙ x

Hier geven de suspensieve punten aan dat "x" met zichzelf "n" moet worden vermenigvuldigd, dat wil zeggen, zo vaak als de exponent het aangeeft.

Enkele eenvoudige voorbeelden van "X Squared", met cijfers, zijn de volgende:

3² = 3 ∙ 3 = 9

(−4)² = (−4) ∙ (−4) = 16

Later worden verschillende toepassingen beschreven waarvoor het nodig is.

Potentiëringseigenschappen

Over het algemeen, het product van elk bedrag met zichzelf, n keer, wordt het potentiëring genoemd. De berekening van X Squared is slechts een bepaald geval van potentiëring, twee andere gevallen verschijnen wanneer u een bedrag wilt verhogen tot exponent 1, waardoor hetzelfde bedrag wordt verkregen:

Kan u van dienst zijn: wetten van exponenten

Aangezien deze bewerkingen frequent zijn, om met bases en exponenten te werken, worden enkele eenvoudige bedieningsregels gevolgd, genaamd Wetten van de exponenten, die hieronder worden vermeld:

Wetten van de exponenten

In wat volgt, "x" is de basis en "n" en "m" zijn de exponenten.

1.- Product van gelijke basismachten

Door twee (of meer) krachten van gelijke basis te vermenigvuldigen, wordt de basis verhoogd tot de som van de exponenten verkregen:

X^N∙ x^M = x^n+m

In het geval van X High wordt deze regel als volgt toegepast, ter vervanging van N en M voor 1:

X¹∙ x¹ = x¹⁺¹ = x²

2.- Bevoegdverdeling van gelijke basis

Door machten van dezelfde basis te verdelen, wordt de basis verkregen, verhoogd tot de aftrekking tussen de respectieve exponenten van de teller en de noemer:

X^N ÷ x^M = x^N-M

Aangezien de divisie door 0 niet wordt gedefinieerd, moet deze worden vervuld, op voorwaarde dat x ≠ 0.

3.- Kracht van een kracht

Het resultaat van het vermogen van een vermogen is gelijk aan de basis die is verheven tot het product van de exponenten:

(X^M))^N = x^M∙N

Het kan opnieuw worden verkregen x vierkant, bij het doen van m = 1 en n = 2:

(X¹))² = x^1∙2 = x²

4.- Negatieve exponent

Voor negatieve exponenten is de te uitvoeren bewerking:

Wanneer x ≠ 0. Merk op dat het vermogen in dit geval een fractie wordt met een teller gelijk aan 1.

5.- Fractionele exponent

Fractionele exponenten kunnen worden geschreven als de nde wortel van de basis:

Op voorwaarde dat n verschilt van 0. Deze waarde wordt de root -index, terwijl M de exponent wordt van de hoeveelheid onder de root, die in dit geval x is.

Kan u van dienst zijn: wat is de richtlijn? (Geometrie)

Producten en quotiënten van verschillende bases

Wanneer u producten en quotiënten van verschillende "X" en "Y" -bases moet verbeteren, worden deze regels gevolgd:

1.- Productkracht

Om dit vermogen uit te voeren, wordt elke hoeveelheid verhoogd tot de exponent n en het resulterende product is vastgesteld:

(x ∙ y)^N = x^N ⋅ en^N

2.- Verhouding van het quotiënt

Nogmaals, elk bedrag moet worden verhoogd tot de exponent n afzonderlijk en het quotiënt vaststellen dat resulteert, volgens de regel dat het bedrag "y" verschilt van 0, in het geval van positieve "n":

(x ÷ y)^N = x^N ÷ y^N

Wanneer "N" negatief is, moet voorzichtigheid worden gebracht, vanwege eigenschap 4 van de vorige sectie, wordt de teller een noemer. In dit geval moeten beide bedragen verschillen van 0, omdat de divisie met 0 kosteloos moet worden vermeden.

Voorbeelden

Voorbeeld 1: vierkanten van natuurlijke getallen

De vierkanten van de eerste tien natuurlijke nummers zijn:

• 1²= 1 × 1 = 1
• 2²= 2 × 2 = 4
• 3²= 3 × 3 = 9
• 4²= 4 × 4 = 16
• 5²= 5 × 5 = 25
• 6²= 6 × 6 = 36
• 7²= 7 × 7 = 49
• 8²= 8 × 8 = 64
• 9²= 9 × 9 = 81
• 10²= 10 × 10 = 100

Voorbeeld 2: het vierkant van negatieve getallen

Het kwadraat van een negatief getal is altijd positief, omdat daarom twee hoeveelheden gelijk worden vermenigvuldigd:

(-x) · (-x) = x ∙ x = x²

Bijvoorbeeld:

(-2) · (-2) = (-2)² = 4

Voorbeeld 3: Vierkant van de som en het verschil

Het is vaak nodig om het kwadraat van de som van twee hoeveelheden, of het verschil, bewerkingen die zijn opgenomen in de categorie opmerkelijke producten te berekenen.

De bewerking wordt opgelost met de gegeven indicaties en de hulp van distributieve eigenschap:

Vierkant van de som

Laat twee "x" en "y" bedragen, en u wilt het kwadraat van zijn som vinden (x + y)²:

Kan u van dienst zijn: hiërarchie van operaties

(x + y)² = (x + y) ∙ (x + y) = x ∙ x + x ∙ y + y ∙ x + y ∙ y = x² + 2x ∙ y + en²

Deze uitdrukking luidt als volgt: "Vierkant van de eerste, plus het dubbele product van de eerste voor de tweede plus het vierkant van de tweede".

Vierkant van verschil

Het wordt analoog opgelost, maar rekening houdend met het negatieve teken:

(x - y)² = (x - y) ∙ (x - y) = x ∙ x - x ∙ y + y ∙ x - y ∙ y = x² - 2x ∙ en + en²

Voorbeeld 4: het gebied van een vierkant

Het vierkant is een 4 -zijdige polygoon, die dezelfde maatregel heeft. Laat ℓ de zijmeting zijn, dan wordt gebied A van de figuur gegeven door:

A = ℓ²

Voorbeeld 5: Pythagoras Stelling

Deze stelling is van toepassing op rechthoekige driehoeken, die waarop twee van zijn zijden rechtstreeks hoek vormen. Deze zijden staan ​​bekend als "categorieën" en de resterende zijde is de "hypotenuse".

De stelling stelt vast dat het kwadraat van de hypotenusa gelijk is aan de som van de vierkanten van de categorieën. 'A' en 'B' naar de categorieën noemen, en 'C' naar de hypotenuse, is de stelling geschreven als:

C² = a² + B²

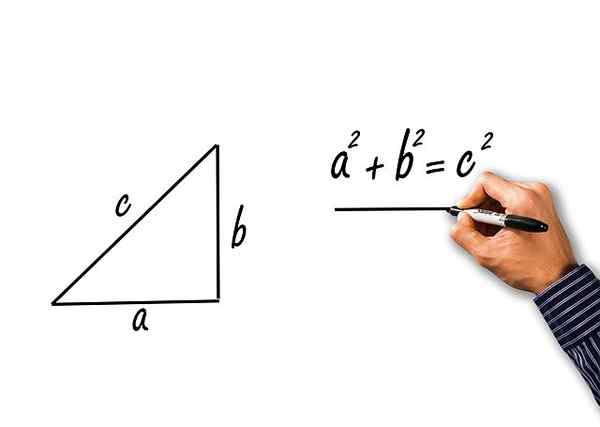Pythagoras Stelling voor een rechthoekige driehoek van katten A en B, en hypotenusa c

Opgeloste oefeningen

Oefening 1

Bereken het kwadraat van de hypotenuse waarvan de benen 3 en 5 eenheden meet.

Oplossing

Volgens de stelling van Pythagoras is het plein van de hypotenuse:

C² = A² + B²

De waarden vervangen:

C² = 3² + 5²= (3 × 3) + (5 × 5) = 9 + 25 = 34

Oefening 2

Bepaal het gebied van een zijkantoor ℓ = 6 cm

Oplossing

A = ℓ² = (6 cm)² = 36 cm²