Karakteristieke eenheidsvectoren, hoe het eruit te krijgen, voorbeelden

De eenheidsvectoren zijn die wiens module, grootte of grootte gelijk is aan de numerieke waarde één. De eenheidsvectoren zijn nuttig om de richting van andere niet -eenheid vectoren aan te geven.

Bedenk dat vectoren wiskundige entiteiten zijn die wiskundig de fysieke magnitudes weergeven die afhankelijk zijn van richting, zoals sterkte, snelheid, versnelling en andere.

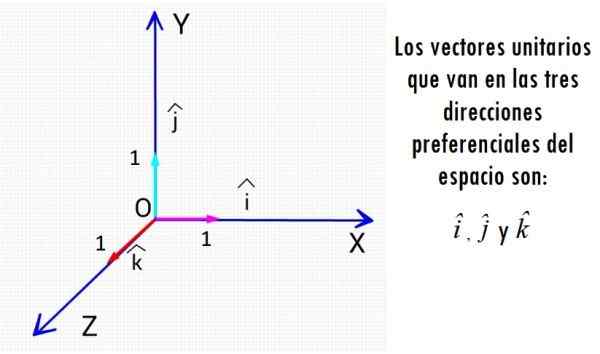
De bekendste eenheidsvectoren zijn de drie vectoren die in de richtingen van de Cartesiaanse assen gaan. Bron: f. Zapata.

Ongeacht de fysieke omvang die geassocieerd is, zijn de eenheidsvectoren entiteiten die eenheden van maatregelen missen en hun grootte is altijd 1, een puur aantal.

De snelheid van een deeltje dat bij 3 m/s beweegt en in de positieve richting van de Cartesiaanse X -as gaat, wordt aangeduid: v = (3 m/s) Je, waarbij de gewaagde letter wordt gebruikt om de vectorbedragen aan te duiden. In dit voorbeeld de module van v Het is 3 m/s en de eenheidsvectormodule Je is 1 (zonder eenheden).

[TOC]

Module, richting en betekenis

Gezien het belangrijke. Op het moment van het weergeven van een vectorbedrag is het noodzakelijk om deze aspecten duidelijk aan te geven.

Nu kan een eenheidsvector elke richting en de betekenis hebben die de voorkeur heeft, maar de grootte moet altijd gelijk zijn aan 1.

Eenheidsvectoren worden gebruikt om een ​​privéadres in de ruimte of in het vlak aan te geven. Als we bijvoorbeeld moeten werken met alle krachten die langs de horizontale as werken, omdat een eenheidsvector in die richting ons helpt deze krachten te onderscheiden van anderen gericht in een andere richting.

En om ze te onderscheiden van niet -eenheid vectoren, wordt de BOLD meestal gebruikt in print en plaatst u een circumflex -accent bovenop, bijvoorbeeld:

Het kan u van dienst zijn: Stationaire staatstheorie: geschiedenis, uitleg, nieuws

Voor handgeschreven teksten is het voldoende om de circumflejo te plaatsen om te begrijpen dat het een eenheidsvector is.

Kenmerken van een eenheidsvector

Wiskundig de eenheidsvector:

Het is een element dat tot een vectorruimte ℛ van dimensie n behoort, zodat |v| = 1, waarbij de balken "module" betekenen.

Dus we kunnen vaststellen dat:

-De unitaire vectormodule is altijd 1, het maakt niet uit of het een sterkte, snelheid of andere vector is.

-Eenheidsvectoren hebben een bepaalde richting, evenals richting, zoals de eenheidsvector in de verticale richting, die kan worden opgelopen of omlaag.

-Eenheidsvectoren hebben een punt van oorsprong. Wanneer weergegeven door een Cartesiaans coördinatensysteem, valt genoemde punt samen met de oorsprong van het systeem: (0.0) als het het vlak of (0,0,0) is als de vector zich in de drie -dimensionale ruimte bevindt.

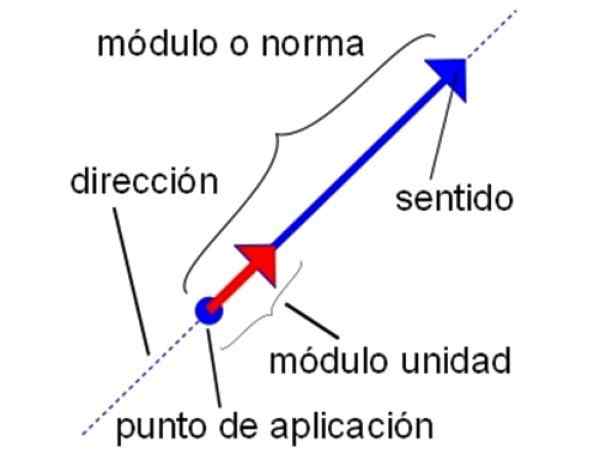De kenmerken van de eenheidsvector. Bron: Wikimedia Commons.

-Ook met de eenheidsvectoren kunnen alle bewerkingen van som, aftrekking en vector vermenigvuldiging die door reguliere vectoren worden gemaakt, worden uitgevoerd. Daarom is het geldig om de eenheidsvector te vermenigvuldigen met een scalair, en het puntproduct en het kruisproduct uit te voeren.

-Met een eenheidsvector in een bepaalde richting kunnen ook andere vectoren worden uitgedrukt die ook in die richting zijn georiënteerd.

De eenheidsvectoren in de ruimte

Om een ​​vector in de ruimte of in het vlak uit te drukken, kunt u een reeks unitaire vectoren loodrecht op elkaar gebruiken, die een ortonormale basis vormen. Elk van de drie voorkeursrichtingen heeft een eigen eenheidsvector.

Laten we teruggaan naar het voorbeeld van de krachten die langs de horizontale as zijn gericht. Dit is de X -as, die twee mogelijkheden heeft: richting rechts en richting links. Stel dat er een eenheidsvector op de X -as is en naar rechts gericht, die we door een van deze vormen kunnen aangeven:

Kan u van dienst zijn: Thomson Atomic Model: kenmerken, postulaten, subatomaire deeltjes

Elk van hen is geldig. Stel nu een kracht F₁ van grootte 5 n langs deze as en naar rechts gericht, kan een dergelijke kracht worden uitgedrukt als:

Als de kracht langs de X -as zou worden gericht, maar in de tegenovergestelde richting, dat wil zeggen links, dan kan een negatief teken worden gebruikt om dit verschil vast te stellen.

Een kracht van 8 N bijvoorbeeld, op de X -as en naar links gericht, zou bijvoorbeeld zo zijn:

Of zo:

En voor vectoren die niet langs de Cartesiaanse bijlen zijn gericht, is er ook een manier om ze te vertegenwoordigen in termen van de orthogonale eenheidsvectoren, via hun Cartesiaanse componenten.

Hoe u de eenheidsvector kunt verwijderen/berekenen?

Om de eenheidsvector te berekenen in de richting van elke willekeurige vector v, De volgende formule wordt toegepast:

Waar:

Het is de module of grootte van de vector v, wiens vierkant als volgt wordt berekend:

|v|² = (v_X))² +  (v_En))²+  ((v_Z))²

Een willekeurige vector in termen van de eenheidsvector

Als alternatief de vector v Het kan als volgt worden uitgedrukt:

Dat wil zeggen het product van zijn module door de bijbehorende eenheidsvector. Dit is precies wat er eerder werd gedaan, wanneer het sprak over de kracht van 5 N van grootte gericht langs de positieve X -as.

Grafische weergave

Grafisch, wat er wordt gezegd, wordt gezien in deze afbeelding, waar de vector v Het is blauw en de bijbehorende eenheidsvector in zijn richting is in rood.

In dit voorbeeld is de vector v Het heeft een grootte groter dan die van de eenheidsvector, maar de verklaring is zelfs geldig als dit niet gebeurt. Met andere woorden, we kunnen vectoren hebben die bijvoorbeeld 0 zijn.25 keer de eenheidsvector.

Kan u van dienst zijn: gewicht (fysiek): berekening, eenheden, voorbeelden, oefeningen

Voorbeelden van eenheidsvectoren

De loodrechte eenheidsvectoren I, J en K

Zoals we eerder hebben gezien, loodrechte eenheidsvectoren Je, J En k Ze zijn erg handig om een ​​andere vector in het vlak of de ruimte weer te geven en vectorbewerkingen uit te voeren. In termen van genoemde vector wordt een willekeurige vector v weergegeven als:

v = V_X Je + v_En J + v_Z k

Waar v_X, v_En en v_Z zijn de rechthoekige componenten van de vector v, die beklimmen -Bold worden niet gebruikt om ze in gedrukte tekst weer te geven-.

De wet van Coulomb

Unitaire vectoren verschijnen vaak in de natuurkunde. Daar hebben we bijvoorbeeld de wet van Coulomb die kwantitatief de interactie beschrijft tussen twee specifieke elektrische ladingen.

Het geeft aan dat de kracht F van aantrekkingskracht of afstoting tussen deze belastingen is evenredig met het product ervan, omgekeerd evenredig met het kwadraat van de afstand die ze scheidt en wordt gericht in de richting van de eenheidsvector die de belastingen aansluit.

Deze vector wordt meestal vertegenwoordigd door:

En de wet van Coulomb is zo, in een vectorvorm:

Waar k Het is de elektrostatische constante, Q₁ En Q₂ Zij zijn de ladingen en R Het is de afstand die hen scheidt.

Oefening opgelost

Vind de eenheidsvector in de richting van de vector v = 5Je + 4J -8k, Gegeven in willekeurige eenheden.

Oplossing

De definitie van eenheidsvector hierboven wordt hierboven toegepast:

Maar eerst moet u de vectormodule berekenen, die zoals deze drie componenten heeft, wordt bepaald door:

|v|² = (v_X))² +  (v_En))² +  (v_Z))²

Verblijven:

|v|² = (5)² +  (4)² +  (-8)²= 25 + 16 + 64 = 105

Daarom de module van v is:

|v| = √105

De door een unitaire vector gezochte is eenvoudig:

Dat leidt ons uiteindelijk naar:

v = 0.488 Je + 0.390 J - 0.781 k

Referenties

1. Bauer, W. 2011. Fysica voor engineering en wetenschappen. Deel 1. MC Graw Hill.
2. Bedford, 2000. NAAR. Mechanica voor engineering: statisch. Addison Wesley.
3. Figueroa, D. (2005). Serie: Physics for Science and Engineering. Deel 1. Kinematica. Uitgegeven door Douglas Figueroa (USB).
4. Giambattista, een. 2010. Natuurkunde. 2e. ED. McGraw Hill.
5. Resnick, r. (1999). Fysiek. Vol. 1. 3e ed. in het Spaans. Continental Editorial Company s.NAAR. van C.V.