Gelijktijdige vectoren kenmerken, voorbeelden en oefeningen

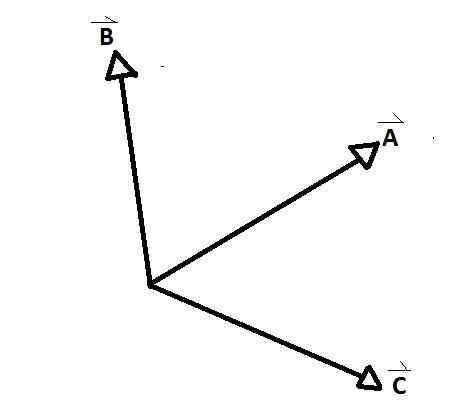
De gelijktijdige vectoren Het zijn de groepen vectoren waarvan de bijlen op een bepaald punt samenvallen en zich tussen elk paar van hen een interne en een externe hoek vormen. Een duidelijk voorbeeld wordt waargenomen in de onderste figuur, waarbij A, B en C gelijktijdige vectoren met elkaar zijn.

D en E In tegenstelling tot de rest zijn dat niet. Er zijn hoeken gevormd onder gelijktijdige vectoren AB, AC en CB. Relatiehoeken tussen vectoren worden genoemd.

[TOC]

Kenmerken

-Ze hebben een gemeenschappelijk punt, dat samenvalt met hun oorsprong: alle grootten van de gelijktijdige vectoren beginnen vanuit een gemeenschappelijk punt naar hun respectieve uitersten.

-De oorsprong wordt beschouwd als het vectoractiepunt: er moet een actiepunt worden vastgesteld dat rechtstreeks door elk van de gelijktijdige vectoren zal worden beïnvloed.

-Uw domein in het vlak en de ruimte is R² en r³ respectievelijk: gelijktijdige vectoren zijn vrij om de hele geometrische ruimte te dekken.

-Maakt verschillende notaties mogelijk in dezelfde groep vectoren. Volgens de takken van de studie zijn verschillende notaties aanwezig in operaties met vectoren.

Soorten vectoren

De tak van de vectoren heeft meerdere onderverdelingen, onder sommigen kunnen ze worden benoemd: de parallelle, loodrechte, coplanarios, overeenkomend, tegenover en eenheid. Gelijktijdige vectoren verschijnen op deze lijst en zoals al die eerder benoemde, hebben ze veel toepassingen in verschillende wetenschappen.

Ze zijn heel gebruikelijk in de vectorstudie, omdat ze een winstgevende generalisatie vertegenwoordigen in de operaties met hen. Zowel in het vlak als in de ruimte zijn gelijktijdige vectoren voor actueel gebruik voor de weergave van verschillende elementen en bestuderen hun invloed op een bepaald systeem.

Vectornotatie

Er zijn verschillende manieren om een ​​vectorelement weer te geven. De belangrijkste en bekendste zijn:

Cartesiaans

Voorgesteld door dezelfde wiskundige benadering, geeft vectoren aan met een lijst die overeenkomt met de magnitudes van elke as (x, y, z)

A: (1, 1, -1) Ruimte A: (1, 1) Plan

Polair

Ze dienen alleen om vectoren in het vlak aan te duiden, hoewel in de integrale berekening de dieptecomponent is toegewezen. Het bestaat met een lineaire omvang R en een hoek ten opzichte van de polaire as Ɵ.

Kan u van dienst zijn: Inferentiële statistieken: geschiedenis, kenmerken, waarvoor is het voor voorbeelden

A: (3, 45⁰ ) Plan A: (2, 45⁰ , 3) ruimte

Analytisch

Definieer de magnitudes van de vector door de versoren. De versoren (R&E + K) vertegenwoordigen de eenheidsvectoren die overeenkomen met de assen X, Y En

A: 3i + 2J - 3K

Bolvormig

Ze zijn vergelijkbaar met polaire notatie, maar met de toevoeging van een tweede hoek die in het vliegtuig veegt XY gesymboliseerd door δ.

A: (4, 60^of , π/4)

Bewerkingen met gelijktijdige vectoren

Gelijktijdige vectoren worden meestal gebruikt om bewerkingen tussen vectoren te definiëren, omdat het gemakkelijker is om de elementen van de vectoren te vergelijken wanneer ze op een gelijktijdige manier voorkomen.

Som (a + b)

De som van gelijktijdige vectoren is bedoeld om de resulterende vector te vinden V_R. Die, volgens de studietak, overeenkomt met een laatste actie

Bijvoorbeeld: 3 snaren zijn gebonden a, b, c aan een doos, elk uiteinde van het touw is in handen van een onderwerp. Elk van de 3 onderwerpen moet het touw in een andere richting trekken dan de andere 2.

A: (Axe, Ay, Az) B: (Bx, By, Bz) C: (Cx, Cy, Cz)

A+b+c = (ax+bx+cx; ay+door+cy; az+bz+cz) = V_R

De doos kan daarom slechts in één richting bewegen V_R zal de richting en het gevoel van de verplaatsing van de doos aangeven.

Verschil (a - b)

Er zijn veel criteria met betrekking tot het verschil tussen vectoren, veel auteurs kiezen ervoor om het uit te sluiten en beweren dat alleen de som tussen vectoren wordt bepaald, waarbij het verschil de som van de tegenovergestelde vector is. De waarheid is dat algebraïsch vectoren kunnen worden afgetrokken.

A: (Axe, Ay, Az) B: (BX, BY, BZ)

A-b = a + (-b) = (ax-bx; ay-be; az-bz) = [ax + (-bx); Ay + (-By); az + (-bz)]

Scalair product (a . B)

Ook bekend als Punto -product, genereert een scalaire waarde die kan worden gerelateerd aan verschillende magnitudes volgens de studietak.

Voor geometrie geeft het parallellogramgebied aan dat wordt gevormd door het paar gelijktijdige vectoren via de parallellogrammethode. Voor mechanische fysica definieert het werk dat door een kracht is gedaan F Door een lichaam op een afstand te bewegen Δr.

Het kan u van dienst zijn: samengestelde evenredigheid: uitleg, drie samengestelde regel, oefeningen

ѡ = f . Δr

Zoals de naam al aangeeft, genereert het een scalaire waarde en wordt het als volgt gedefinieerd:

Wees de vectoren a en b

A: (Axe, Ay, Az) B: (BX, BY, BZ)

-Analytische vorm:

( NAAR . B) = | a |.| B |.Cos θ

Waarbij θ de interne hoek is tussen beide vectoren

-Algebraïsche vorm:

( NAAR . B) = (bijl.Bx + ay.door + az.BZ)

Vectorproduct (a x b)

Het vector- of puntproduct tussen twee vectoren, definieert een derde vector C dat heeft de kwaliteit van loodrecht op B En C. In de natuurkunde definieert het vectormoppel τ Basiselement van rotatiedynamiek.

-Analytische vorm:

| A X B | = | A |.| B |.Sin θ

-Algebraïsche vorm:

(A x b) = = = (Bijl . door - ay . bx)- (bijl . BZ - AZ . bx) J + (Bijl . door - ay . bx) k

-Relatieve beweging: r_A/B

De basis van relativiteit is de relatieve beweging en de gelijktijdige vectoren vormen de basis van de relatieve beweging. U kunt posities, snelheden en relatieve versnellingen afleiden door de volgende volgorde van ideeën toe te passen.

R _A/B = r_NAAR - R_B    ; Relatieve positie met betrekking tot B

v _A/B = V_NAAR - v_B  ; Relatieve snelheid van respect voor B

naar _A/B = a_NAAR - naar_B  ; Relatieve versnelling van respect voor B

Voorbeelden: opgeloste oefeningen

Oefening 1

Laat A, B en C gelijktijdige vectoren.

A = (-1, 3, 5) B = (3, 5, -2) C = (-4, -2, 1)

-Definieer de resulterende vector V_R = 2a - 3b + c

2a = (2 (-1), 2 (3), 2 (5)) = (-2, 6, 10)

-3b = (-3 (3), -3 (5), -3 (-2)) = (-9, -15, 6)

V_R = 2a + (-3b) + c = (-2, 6, 10) + (-9, -15, 6) + (-4, -2, 1)

V_R = ([-2+(-9)+(-4)]; [6+(-15)+(-2)]; (10+6+1))

V_R = (-15, -11, 17)

-Definieer het scalaire product (a . C)

( NAAR . C) = (-1, 3, 5) . (-4, -2, 1) = (-1) (-4) + 3 (-2) + 5 (1) = 4-6 + 5

( NAAR . C) = 3

-Bereken de hoek tussen a en c

( NAAR . C) = | a |.| C |.Cos θ waarbij θ de kortste hoek is tussen vectoren

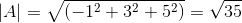
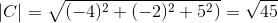
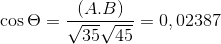
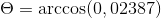
θ = 88.63⁰

 -Vind een vector loodrecht op A en B

Hiervoor is het noodzakelijk om het vectorproduct te definiëren tussen (-1, 3, 5) en (3, 5, -2). Zoals eerder uitgelegd, wordt een 3 x 3 matrix gebouwd waar de eerste rij bestaat uit de lijst met eenheidsvectoren (i, j, k). Dan bestaat de 2e en 3e rij uit de te bedienen vectoren, met respect voor de operationele orde.

Kan u van dienst zijn: decimale notatie

(A x b) = = [(-1) . 5 - (3 . 3)] Je  - [(-1) . (-2) - (5 . 3)] J + [(-1) . 5 - (3 . 3)] k

(A x b) = (-5 - 9) Je - (2 - 15) J + (-5 - 9) k         

(A x b) =  -14 i + 13 j - 14 k

Oefening 2 

Laat V_naar en v_B De snelheidsvectoren van respectievelijk a en b. Bereken de B -snelheid van a.

V_naar = (3, -1, 5) v_B = (2, 5, -3)

In dit geval wordt de relatieve snelheid van B gevraagd V_B/a

V_B/a = V_B - V_NAAR

V_B/a = (2, 5, -3) -(3, -1, 5) = (-1, 6, -8)

Dit is de Veloc Vector van B gezien vanuit een. Waarbij een nieuwe vector van de B -snelheid wordt beschreven door verwijzing naar een waarnemer geplaatst in A en beweegt met de snelheid van een.

Voorgestelde oefeningen

1-construct 3 vectoren A, B en C die gelijktijdig zijn en 3 operaties tussen hen relateren via een praktische oefening.

2 -vectoren A: (-2, 4, -11), B: (1, -6, 9) en C: (-2, -1, 10). Zoek loodrechte vectoren aan: A en B, C en B, Sum A + B + C.

4-determine 3 vectoren die loodrecht op elkaar staan, zonder rekening te houden met de coördinaatassen.

5 definiëren het werk dat wordt gedaan door een kracht die een massablok van 5 kg optilt, vanaf de bodem van een diepe put van 20 meter.

6-Swamker-algebraïsche dat de aftrekking van vectoren gelijk is aan de som van de tegenovergestelde vector. Rechtvaardigen uw postulaten.

7-Denote een vector in alle notaties die in dit artikel zijn ontwikkeld. (Cartesian, Polar, Analytics and Sferical).

8-De magnetische krachten die worden uitgeoefend op een magneet die op een tafel rust, wordt gegeven door de volgende vectoren; V: (5, 3, -2), t: (4, 7, 9), h: (-3, 5, -4). Bepaal in welke richting de magneet zal bewegen als alle magnetische krachten tegelijkertijd werken.

Referenties

1. Euclidische geometrie en transformaties. Clayton W. Slimmigheidje. Couer Corporation, 1 januari. 2004
2. Hoe op te lossen Mathematica Problemen toepassen L. Moiseiwitsch. Couer Corporation, 10 april. 2013
3. Basisconcepten van geometrie. Walter Prenowz, Meyer Jordan. Rowman & Littlefield, 4 oktober. 2012
4. De vectoren. Rocío Navarro Lacoba, 7 juni. 2014
5. Lineaire algebra. Bernard Kolman, David R. HEUVEL. Pearson Education, 2006