A rhomboid Het is een vlakke figuur van vier zijden, -a vierhoekig -in waarvan de zijkanten en de interne hoeken zijn twee tot twee verschillend. Daarom behoort de rhomboid tot de groep schuine parallellogrammen.

Geometrische cijfers maken deel uit van de natuur en in het bijzonder die van vier zijden zoals de rhomboid, hebben veel toepassingen in architectuur en ontwerp.

Figuur 1. De lichtpanelen van het Allianz Arena Stadium in München, Duitsland, verlichten met de kleuren van het lokale team en met wit licht wanneer de selectie van dat land speelt. Bron: Pxhere.

We hebben een deel van de gevel van het Allianz Arena Football Stadium in München. Het zijn rhomboid -panelen die oplichten met de kleuren van het lokale team.

Het is daarom een ​​figuur met veel visuele dynamiek, omdat het, in tegenstelling tot andere vierhoekige vierkanten, geen symmetrieas heeft. De volgende figuur toont verschillende rhomboids met gevarieerde oriëntaties in het vlak.

Figuur 2. Verschillende rhomboid met verschillende oriëntaties in het vlak. Bron: f. Zapata.

[TOC]

Romboid -kenmerken

Vervolgens de belangrijkste kenmerken van deze interessante geometrische figuur:

-Bladnummer: 4.

-Aantal hoekpunten: 4.

-De tegenoverliggende zijden zijn hetzelfde en parallel, maar de aangrenzende kanten zijn ongelijk.

-Het heeft 4 interne hoeken: twee acute (minder dan 90º), aangegeven door de Griekse letter α en twee stompe (meer dan 180º), β genoemd (zie figuur 3).

-Door twee aaneengesloten hoeken van de rhomboid toe te voegen, wordt 180º verkregen, daarom zijn α en β Aanvullend.

-De som van de 4 interne hoeken is gelijk aan 360º.

-Een diagonaal is een segment dat begint bij een hoekpunt en eindigt bij het tegenovergestelde hoekpunt.

-Het punt waarop de diagonalen van de rhomboid kruising worden genoemd barycenter.

-De rhomboid -diagonalen hebben verschillende maten.

Over de diagonalen van de rhomboid zijn er enkele belangrijke details die we hieronder zullen bespreken.

Kan u van dienst zijn: in afwachting van een lijn: formule en vergelijkingen, representatie, voorbeelden

Diagonalen van de rhomboid

Het is heel belangrijk om te benadrukken dat de diagonalen van de rhomboids niet bisectrical zijn, dat wil zeggen dat ze de interne hoeken van de figuur niet in twee gelijke delen verdelen.

De diagonalen staan ​​niet loodrecht op elkaar. We kunnen ze echter gemakkelijk berekenen met de cosinus -stelling. Dus de belangrijkste diagonale D_M In de rhomboid van figuur 3 is:

D_M = √ (a² + B² - 2.Aab.cos β)

En de kleine diagonale D_M Ik zou zijn:

D_M = √ (a² + B² - 2.Aab.cos α)

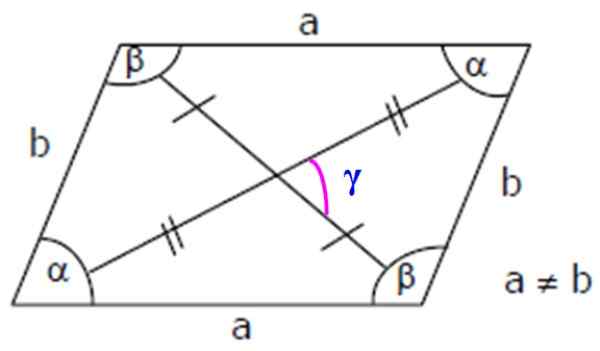figuur 3. Romboid -elementen: zijden, interne en diagonale hoeken. Bron: Wikimedia Commons.

Belangrijk: Aangezien α en β aanvullend zijn, wordt vervuld dat:

sin α = sin β

cos α = -cos β

Deze eigenschappen van trigonometrische redenen moeten in aanmerking worden genomen bij het oplossen van de oefeningen.

Hoe u de perimeter en het gebied uithaalt

Om de perimeter en het gebied te vinden dat we de zijkanten van de rhomboid zullen geven, zullen deze zijn naar En B. We hebben ook de hoogte van de rhomboid, genoemd H, die de lijn is die uit een van de hoekpunten is getrokken en loodrecht op de andere kant van de figuur is gericht.

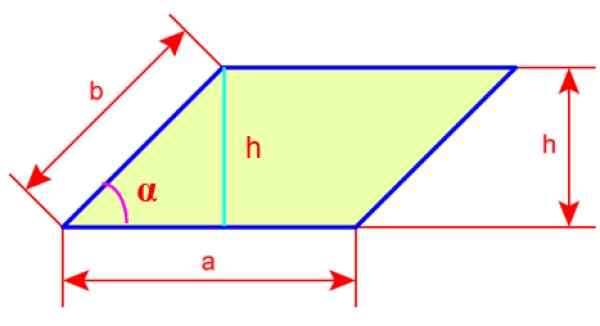Figuur 4. Zijkanten en rhomboidhoogte. Bron: Wikimedia Commons.

Perimeter van de rhomboid

De omtrek van de rhomboid wordt berekend door de lengtes van zijn vier zijden toe te voegen. Laten we P aan de omtrek bellen, dan:

P = 2A + 2B

We kunnen het ook uitdrukken door:

P = 2 (A+B)

Perimeter die de hoogte kent

Als we er goed uitzien, kan de hoogte h worden bepaald uit de driehoek aan de linkerkant in figuur 4. Zijde B zou de hypotenusa zijn en de hoogte is daarom de cateto die tegen de hoek α was:

sin α = tegenovergestelde / hypotenusa cateto

O goed:

sin α = h / b

Dan wissen we B:

b = h / sin α

We vervangen in de omtrek P:

P = 2 [a + (h / sin α)]]

Romboid gebied

Het rhomboid -gebied is de maat van het oppervlak. En omdat het een parallellogram is, wordt het gebied A gegeven door de goed bekende uitdrukking:

Kan u van dienst zijn: gemeenschappelijke factor voor het groeperen van termen: voorbeelden, oefeningen

A = basis x hoogte

Dat volgens figuren 3 en 4 het wordt uitgedrukt door:

A = a x h

Gebied die beide kanten kent en een interne hoek

Door de basistrigonometrie van de vorige sectie toe te passen, vinden we equivalente uitdrukkingen voor het rhomboid -gebied:

h = B. sin α

Dan is het gebied als volgt:

A = A. B. sin α

Onthouden wat we hierboven hebben gezegd over de aanvullende hoeken, kunnen we sen α vervangen door sen β indien nodig.

Gebied die de diagonalen en de hoek ertussen kent

Ten slotte, als we de diagonalen kennen D_M en D_M, Plus de hoek γ daartussen (zie figuur 3), kan het gebied worden berekend door het semi -product van de diagonalen door de boezem van die hoek:

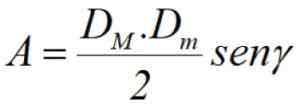
Oefening opgelost

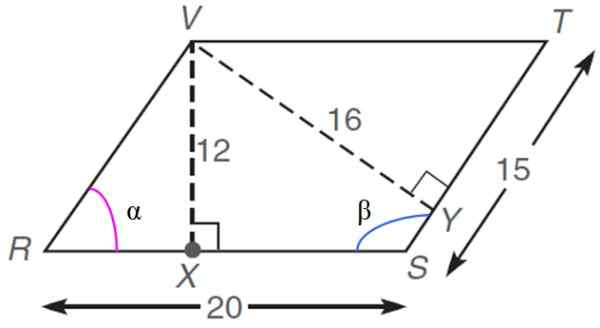
In de volgende rhomboid, wiens afmetingen worden gegeven in willekeurige eenheden of.naar., vinden:

a) de omtrekwaarde

b) het gebied

c) interne hoeken α en β

d) de lengte van het Rx -segment

e) de maat van elk van de diagonalen

Oplossing voor

De omtrek P is:

P = 2 (A + B)

We identificeren eerst de waarden van A en B:

A = 20

B = 15

We vervangen de formule en berekenen:

P = 2. (20 + 15) = 70 u.naar.

Oplossing B

Het diagram biedt hoogte h = 12 u.A, daarom kan het gebied worden berekend met de formule:

A = a x h

A = 20 x 12 u.naar.² = 240 u.naar.²

Ongeacht de geselecteerde eenheid om de zijkanten en hoogte te meten, wordt het gebied altijd uitgedrukt in vierkante eenheden.

Hetzelfde resultaat als u komt bij het berekenen van het gebied met de andere hoogte van de rhomboid, die 16 u waard is.naar. Inderdaad:

A = 16 x 15 u.naar.² = 240 u.naar.²

Oplossing C

De hoek α kan worden berekend door:

Het kan u van dienst zijn: positiemaatregelen, centrale neiging en dispersie

h = B. sin α

Omdat H- en B -waarden daarom bekend zijn:

α = arcsen (h/b) = arcsen (12/15) = 53.13e

Herinnerend dat α- en β -hoeken aanvullend zijn, is het vervuld:

α + β = 180º ⇒ β = 180 - 53.13e = 126.87º

Oplossing D

De RX -segmentlengte wordt gemakkelijk berekend, omdat er voldoende informatie is om deze te vinden. Bijvoorbeeld door:

Rx = rv . cos α = 15 . Cos 53.13e u.naar. = 9 u.naar.

Ook door de stelling van Pythagoras door de rechthoekige driehoek van zijkanten 15 en 12 u.naar:

(RV)² = (Rx)² + H²

De lengte van het belangensegment vrijmaken:

Rx = √ [(RV)² - H²] = √ [15² - 12²] = √81 = 9

Oplossing e

De maat van een van de diagonalen, bijvoorbeeld de diagonale die zich bij de hoekpunten r en t verbindt, die een grote diagonaal is, wordt gegeven door de cosinusstelling, zoals eerder uitgelegd, dus we vervangen daar waarden:

D_M = √ (20² + 25² - 2. twintig. vijftien .Cos 126.87º) = 37.22 U.naar.

Voor de kleine diagonaal:

D_M = √ (20² + 25² - 2. twintig. vijftien .Cos 53.13e) = 25.79 u.naar.

Referenties

1. Alexander, D. 2013. Geometrie. 5e. Editie. Cengage leren.
2. Baldor, een. 1973. Geometrie en trigonometrie. Midden -Amerikaans cultureel redactioneel.
3. EN. NAAR. 2003. Geometrie -elementen: met oefeningen en kompasgeometrie. Universiteit van Medellin.
4. Jiménez, r. 2010. Wiskunde II. Geometrie en trigonometrie. Tweede druk. Prentice Hall.
5. Regelmatige polygonen. Hersteld van: maat.engineering.USAC.Edu.GT.
6. Universe -formules. Rhomboid. Hersteld van: UniversOFormulas.com.
7. Wikipedia. Rhomboid. Hersteld van: is.Wikipedia.borg.