Oblicual Parabolic Shot -kenmerken, formules, vergelijkingen, voorbeelden

Hij Oblicual Parabolic Shot Het is een bepaald geval van de vrije valbeweging waarin de initiële snelheid van het projectiel een bepaalde hoek vormt met de horizontale, wat resulteert in een parabolisch pad.

De vrije val is een geval van beweging met constante versnelling, waarbij versnelling die van de zwaartekracht is, die altijd verticaal naar beneden wijst en een grootte heeft van 9,8 m/s^2. Het hangt niet af van het deeg van het projectiel, zoals Galileo Galilei heeft aangetoond in 1604.

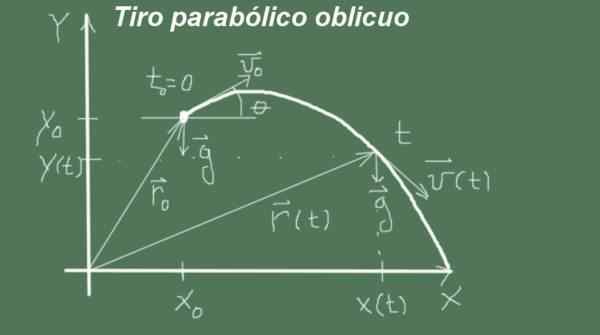
Figuur 1. Oblicual Parabolic Shot. (Eigen uitwerking)

Als de initiële projectielsnelheid verticaal is, heeft de vrije val een recht en verticaal traject, maar als de initiële snelheid dan schuin is, is het traject van vrije val een parabolische curve, ook aangetoond door Galileo.

Voorbeelden van parabolische beweging zijn het traject dat volgt op een honkbal, de kogel afgevuurd door een kanon en de waterstraal die uit een slang komt.

Figuur 1 toont een schuin parabolisch schot van 10 m/s met een hoek van 60º. De schaal bevindt zich in meters en de opeenvolgende P -posities worden genomen met een verschil van 0,1 s vanaf het beginmoment 0 seconden.

[TOC]

Formules

De beweging van een deeltje wordt volledig beschreven als zijn positie bekend is, zijn snelheid en zijn versnelling als een functie van de tijd.

De parabolische beweging als gevolg van een schuin schot is de superpositie van een horizontale beweging met constante snelheid, plus een verticale beweging met constante versnelling gelijk aan de versnelling van de zwaartekracht.

De formules die van toepassing zijn op het schuine parabolische schot zijn degene die overeenkomt met een beweging met constante versnelling A = G, Merk op dat BOLD is gebruikt om aan te geven dat versnelling een vectorbedrag is.

Kan u van dienst zijn: natuurlijke satellieten

Positie en snelheid 

In een constante versnellingsbeweging hangt de positie wiskundig af van de tijd op een kwadratische manier.

Als we aangeven R(T) De positie naar tijd T, Rof De eerste instant positie, vof De eerste snelheid, G versnelling en t = 0 Als het eerste moment de formule die de positie voor elk moment geeft T is:

R(t) = R_of + v_of T + ½ G T²

Vetgedrukt in de vorige uitdrukking duidt op dat het een vectorvergelijking is.

De snelheid als een functie van tijd wordt verkregen door het nemen van het derivaat ten opzichte van de positie en het resultaat is:

v(t) = v_of + G T

En om versnelling te verkrijgen als functie van de tijd, de snelheid afgeleid van T resulterend:

naar(t) = G

Wanneer de tijd niet beschikbaar is, is er een relatie tussen snelheid en positie, die wordt gegeven door:

v² = Vof² - 2 g (en - ik)

Vergelijkingen

Vervolgens zullen we de vergelijkingen vinden die van toepassing zijn op een schuin parabolisch schot in Cartesiaanse vorm.

Figuur 2. Variabelen en parameters van de schuine parabolische schot. (Eigen uitwerking)

De beweging begint op dit moment t = 0 Met de eerste positie (Xo, ik) en magnitude snelheid vof en hoek θ, dat wil zeggen dat de initiële snelheidsvector is (vof cosθ, vof Senθ). De beweging gaat voorbij met versnelling 

G = (0, -g).

Parametrische vergelijkingen

Als de vectorformule die de positie als een functie van de tijd geeft, wordt toegepast en componenten worden gegroepeerd en gelijkgesteld, worden de vergelijkingen gegeven door de coördinaten van de positie tot een tijdstip van tijd t verkregen.

x (t) = x_of + v_os T 

en (t) = y_of + v_Oy t -½ g t²

Evenzo worden vergelijkingen gehad voor snelheidscomponenten als een tijdfunctie.

Het kan u van dienst zijn: normale inspanning: waar het uit bestaat, hoe het wordt berekend, voorbeelden

v_X(t) = V_os

v_En(t) = V_Oy - g t 

Waar: v_os = Vof cosθ; v_Oy = Vof Senθ

Trajectvergelijking

y = a x^2 + b x + c

A = -g/(2 Vos^2)

B = (vOy/Vos + G Xof/Vos^2)

C = (enof - vOy Xof / Vos))

Voorbeelden 

voorbeeld 1

Beantwoord de volgende vragen:

a) Waarom veracht in parabolische schietproblemen meestal het effect van wrijving met lucht?

b) doet de vorm van het object in het parabolische schot?

Antwoorden

a) Voor de beweging van een projectiel dat parabolisch is, is het belangrijk dat de luchtwrijvingskracht veel lager is dan het gewicht van het object dat wordt gelanceerd. 

Als een kurkbal of wat licht materiaal wordt gegooid, is de wrijvingskracht vergelijkbaar met het gewicht en het traject ervan kan een parabool niet benaderen.

Integendeel, als het een zwaar object als een steen is, is de wrijvingskracht te verwaarlozen in vergelijking met het gewicht van de steen en het traject is dicht bij een parabool.

b) De vorm van het gelanceerde object is ook relevant. Als een plata van vliegtuig in de vorm van een Avionncito wordt gelanceerd, is de beweging niet vrij of parabolisch, omdat de vorm de luchtweerstand begunstigt.

Aan de andere kant, als hetzelfde vel papier compact is in de vorm van een bal, is de resulterende beweging erg vergelijkbaar met een parabool.

Voorbeeld 2

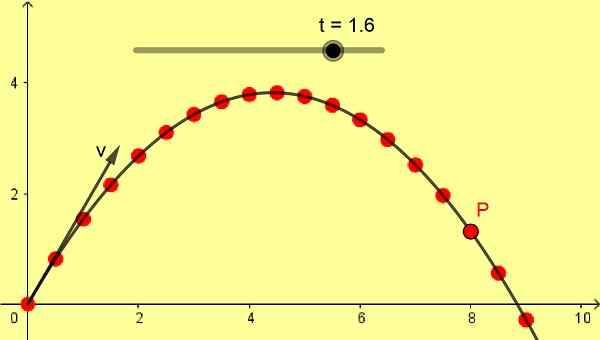
Een projectiel wordt snel vanaf de horizontale vloer gelanceerd van 10 m/s en 60º hoek. Dit zijn dezelfde gegevens waarmee figuur 1 is ontwikkeld. Met deze gegevens vind ik:

a) moment waarop het de maximale hoogte bereikt.

Kan u van dienst zijn: wat zijn de thermische eigenschappen en wat zijn? (Met voorbeelden)

b) de maximale hoogte.

c) de snelheid op de maximale hoogte.

d) De positie en snelheid op 1,6 s.

e) Op het moment dat hij weer grond speelt.

f) horizontale reikwijdte.

Oplossing voor)

De verticale snelheid afhankelijk van tijd is

v_En(t) = V_Oy - G T = V_of Senθ - G T = 10 Sen60º - 9.8 T = 8.66 - 9.8 t 

Op het moment dat de maximale hoogte wordt bereikt, is de verticale snelheid nul voor een ogenblik.   

8.66 - 9.8 t = 0 ⇒ t = 0.88 s.

Oplossing B)

De maximale hoogte wordt gegeven door de coördinaat En Voor het moment waarop die hoogte wordt bereikt:

en (0.88S) = Yo ik zal t -½ g t^2 = 0 + 8.66*0.88-½ 9.8 0.88^2 = 

3.83 m

Daarom is de maximale hoogte 3.83 m.

Oplossing c)

De snelheid op maximale hoogte is horizontaal:

v_X(t) = V_os = V_of cosθ = 10 cos60º = 5 m/s 

D) Oplossing

De positie op 1.6 s is:

X (1.6) = 5*1.6 = 8,0 m

en 1.6) = 8.66*1.6½ 9.8 1.62 = 1.31 m

Oplossing e)

Wanneer de coördinaat raakt en deze wordt geannuleerd, dan:

en (t) = 8.66*T -½ 9.8 t2 = 0 ⇒ t = 1,77 s

Oplossing f)

De horizontale reikwijdte is de X -coördinaten op het moment dat grond speelt:

X (1.77) = 5*1.77 = 8,85 m

Voorbeeld 3

Zoek de trajectvergelijking met voorbeeld 2 -gegevens.

Oplossing 

De parametrische vergelijking van het traject is:

x (t) = 5*t

en (t) = 8.66*T -½ 9.8 t^2

En de Cartesiaanse vergelijking wordt verkregen door T van de eerste op te ruimen en in de tweede te vervangen

y = 8.66*(x/5) --½ 9.8 (x/5)^2

Vereenvoudiging:

y = 1,73 x - 0,20 x^2 

Referenties

1. P. P. Teodorescu (2007). "Kinematica". Mechanische systemen, klassieke modellen: deeltjesmechanica. Springer.
2. Resnick, Halliday & Krane (2002). Fysica Volume 1. CECSA, Mexico.
3. Thomas Wallace Wright (1896). Elementen van mechanica, waaronder kinematica, kinetiek en statica. E en FN Spon.
4. Wikipedia. Parabolische beweging. Hersteld van ES.Wikipedia.borg.
5. Wikipedia. Projectielbeweging.Opgehaald van.Wikipedia.borg.