Soorten functies en hun grafieken

Er zijn divers Soorten functies die worden gebruikt om problemen in takken van kennis te modelleren, zoals natuurwetenschappen, administratie, economie en sociale wetenschappen. Wiskundig gezien is een functie een relatie tussen twee of meer variabelen.

Vaak zijn bepaalde objecten of hoeveelheden aan elkaar gerelateerd. Deze bedragen worden weergegeven door variabelen. Er zijn bijvoorbeeld twee gerelateerde variabelen, behorende tot twee sets A en B, niet noodzakelijk numeriek, hoewel ze meestal zijn-.

Om als een functie te worden beschouwd, moet deze relatie aan twee voorwaarden voldoen: de eerste is dat alle elementen van de startset om deel te nemen, en de tweede, dat elk element van deze set gerelateerd is aan slechts één van de elementen van set B.

Variabelen worden meestal met letters aangeroepen X En En, met X als de onafhankelijke variabele En En als de afhankelijke variabele. Natuurlijk kunnen ze op een andere manier worden aangeroepen en de naam van de variabele kiezen in overeenstemming met de grootte die het vertegenwoordigt.

De relatie tussen de twee wordt aangegeven via de brief F -of een andere letter van het alfabet-, en wordt op verschillende manieren weergegeven, zoals een set geordende paren, een grafiek, een verbale uitdrukking of een algebraïsche formule:

• f (x) = x + 1
• Bevolking P van een bepaalde stad in een bepaald tijdsinterval t.
• H (x) = (1,3); (2,4); (3,5); (4.6)

Functies worden gekenmerkt door te hebben domein En bereik of route. Domein is de set van waarden die de variabele X U kunt nemen, terwijl het bereik de set waarden is die de afhankelijke functie of variabele verwerft en.

Classificatie van functies

De functies kunnen worden gegroepeerd in 5 grote categorieën, zoals weerspiegeld in het volgende schema, waarin elke groep wordt gelabeld met een Romeins nummer en een kleur. Van links naar rechts worden de functies geclassificeerd volgens:

• I) zijn vorm.
• Ii) symmetrie.
• Iii) De manier om de variabele uit te drukken.
• Iv) zijn continuïteit en eentonigheid.
• V) De manier waarop de domeinelementen gerelateerd zijn aan die van het bereik.

Hoofdclassificatiecriteria voor functies. Bron: f. Zapata.

Volg nu een korte beschrijving van elk van de soorten functies met hun respectieve voorbeelden.

I) functioneert volgens zijn vorm

Je.1) Algebraïsche functies

Ze behoren tot de meest gebruikte functies op tal van wetenschapsgebieden, en daarom zijn ze de bekendste. Ze worden gekenmerkt door als een correspondentieregel, een algebraïsche uitdrukking.

Op hun beurt zijn algebraïsche functies onderverdeeld in de volgende typen:

• Je.1.a) polynoom of polynoom.
• Je.1.b) rationeel.
• Je.1.c) irrationeel.
• Je.1.d) door secties.

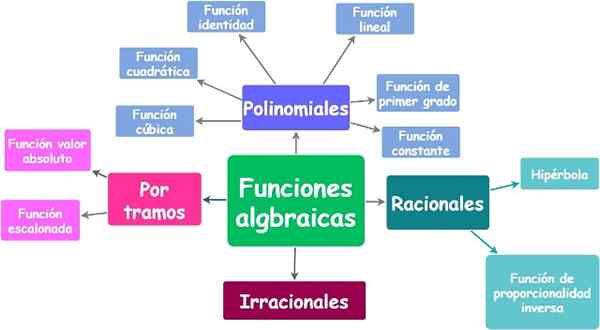Algebraïsche functies en hun typen. Bron: f. Zapata.

Je.1.a) polynoom- of polynoomfuncties

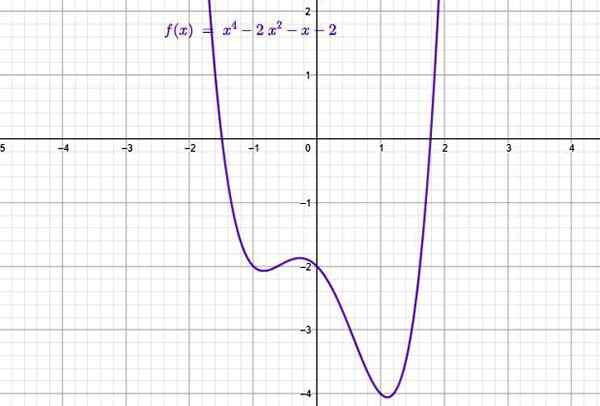Voorbeeld van de functie van het polynoomtype. Bron: f. Zapata door Geogebra.

Ze bestaan ​​uit sommen termen waarvan de algemene vorm is:

P (x) = a_NX^N + naar _N-1X^N-1 +… naar₁x + a₀

Waar de coëfficiënten_N, naar _N-1… naar₁, naar₀ Het zijn reële getallen en n is een geheel getal. Het domein van polynoomfuncties is de set R van reële getallen en zijn ook continue functies in dat domein.

In de bovenste figuur staat de grafiek van de volgende polynoomfunctie van volgorde 4:

f (x) = x⁴ - 2x² - X -2

Onder de polynoomfuncties worden sommige specifieke gevallen onderscheiden, volgens de waarden van de coëfficiënten. Het is de moeite waard om zorgvuldig te overwegen, omdat ze in meerdere situaties erg nuttig zijn:

i) constante functie

Er is een constante functie wanneer alle coëfficiënten worden geannuleerd, behalve₀:

f (x) = a₀ = K

De grafiek van de constante functie is een rechte lijn parallel aan de horizontale as, zoals lijnen:

• f (x) = 2
• g (x) = π
• H (x) = -3/2

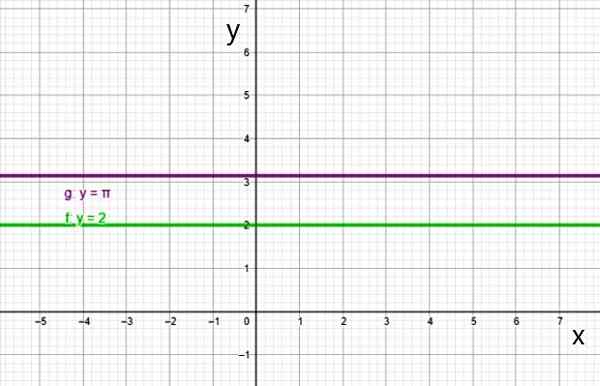Twee voorbeelden van constante functie. Bron: f. Zapata.

Ii) Eerste graadfunctie

De eerste functie -uitroeibare of gerelateerde functie is dat wiens grafiek een rechte lijn is. Het is een bepaald geval van de polynoomfunctie waarbij alle anne -coëfficiënten₁ al₀. Het wordt gegeven door:

f (x) = a₁x + a₀

De waarde a₁ Het is de helling van de lijn, die een maat voor zijn helling geeft, en₀ Het is de snit van de lijn met de verticale as. Beide kunnen positieve of negatieve waarden nemen.

Voorbeelden van eerste graadfunctie zijn de volgende:

• G (x) = 2x -1
• H (x) = -6x +5/2

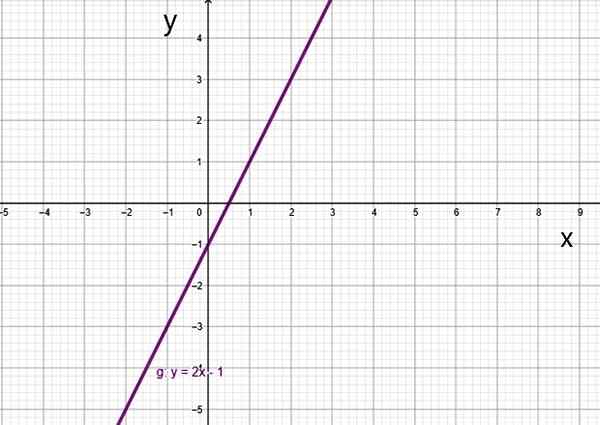Eerste graad functie f (x) = 2x-1. Bron: f. Zapata.

Er is een speciaal geval, wat de lineaire functie is.

Kan u van dienst zijn: centrale neigingsmaatregelen voor gegroepeerde gegevens: formules, oefeningen

iii) lineaire functie

Wanneer de coëfficiënt is₀ Het is 0, de functie gaat altijd door de oorsprong en wordt uitgedrukt door f (x) = a₁X, bellen lineaire functie, Hoe is het:

• f (x) = 5x
• G (x) = -7x

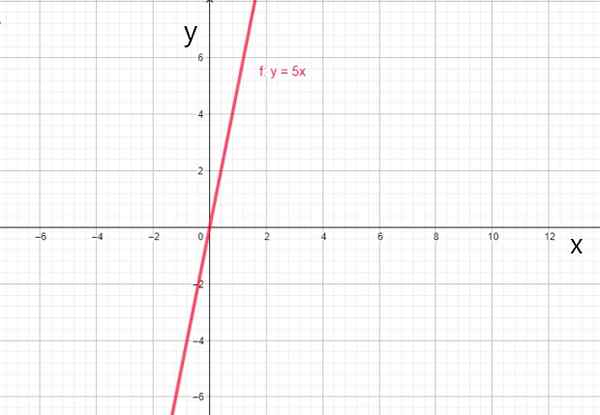Lineaire functie f (x) = 5x. Bron: f. Zapata.

iv) identiteitsfunctie

Het is een bepaald geval van de lineaire functie, waarin₁ = 1:

f (x) = x

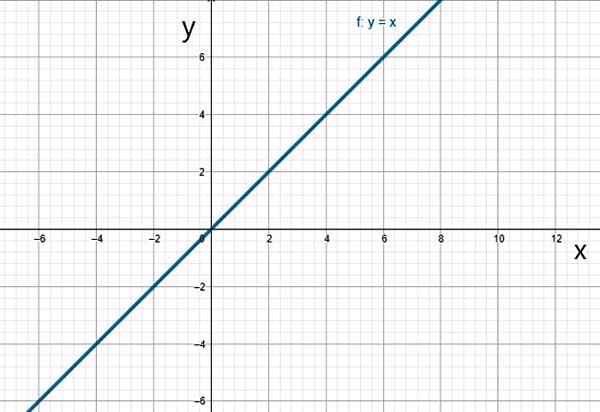De identiteitsfunctie. Bron: f. Zapata.

v) kwadratische functie

Het heeft de algemene vorm:

f (x) = a₂X² +naar₁x + a₀

Met een₂  ≠ 0.

De grafiek is een gelijkenis waarvan de axiale of symmetrieas parallel is aan de as van de ordinaten. Snijdt altijd de verticale as op het coördinaatpunt x = 0, y = a₀. Wat betreft kruispunten met de horizontale as, deze kan maximaal 2 hebben.

Voorbeelden van kwadratische functies zijn:

• f (x) = x² - 3x - 4
• G (x) = 4x²
• H (x) = x²-1

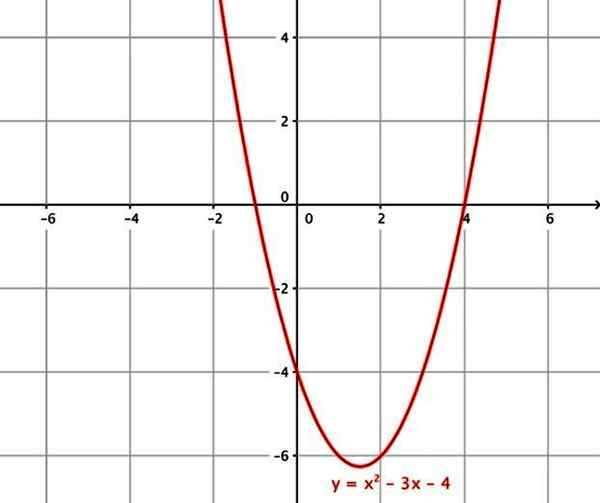De kwadratische functie. Bron: Wikimedia Commons.

vi) kubieke functie

Zoals de naam al aangeeft, bevat de kubieke functie een kracht van 3:

f (x) = a₃X³ + naar₂X² + naar₁x + a₀

De coëfficiënt a₃ Het is altijd anders dan 0, zoals in deze gevallen:

• f (x) = x³
• G (x) = 5x³ - 2
• H (x) = -3x³ + 4x² + 10x + 1

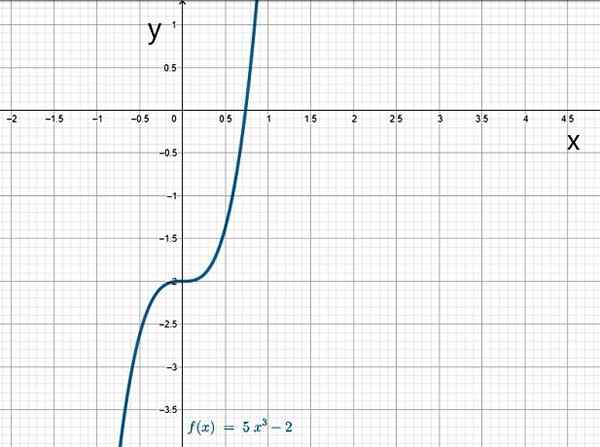Kubieke functie. Bron: f. Zapata.

Je.1.b) Rationele functies

Rationele functies hebben de vorm:

 Waar p (x) en q (x) onherleidbare polynomen zijn, dat wil zeggen dat ze geen gemeenschappelijke factor hebben en in elk geval q (x) ≠ 0.

Uit het domein van rationele functies, alle waarden die de noemer q (x) annuleren, dat wil zeggen zijn wortels, terwijl de waarden van de waarden van de waarden van de waarden van En die de horizontale asymptoten bepalen.

Een asymptoot is een lijn waarop de functie nadert, zowel aan de linkerkant als aan de rechterkant, boven of onder, maar kruist nooit. Dergelijke lijnen kunnen verticaal, horizontaal of hellend zijn.

Voorbeelden van rationele functies zijn:

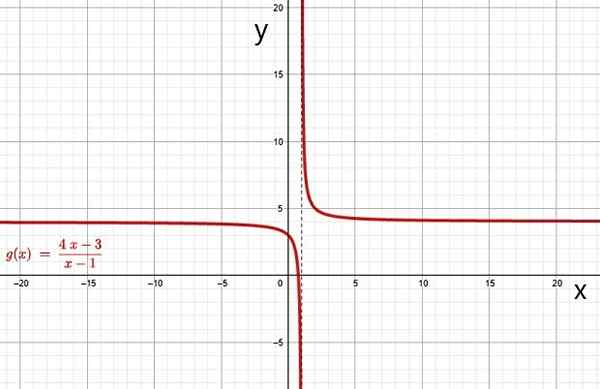Rationele functie. Bron: f. Zapata door Geogebra.

i) HYPERBOLA

De grafiek van een rationele functie is een hyperbool wanneer polynoom in noemer Q (x) graad 1 heeft. De grafiek van de functies f (x) en g (x) van de bovenstaande voorbeelden zijn hyperbolen, het kan eenvoudig worden gecontroleerd via een gratis online grafische software, zoals Geogebra.

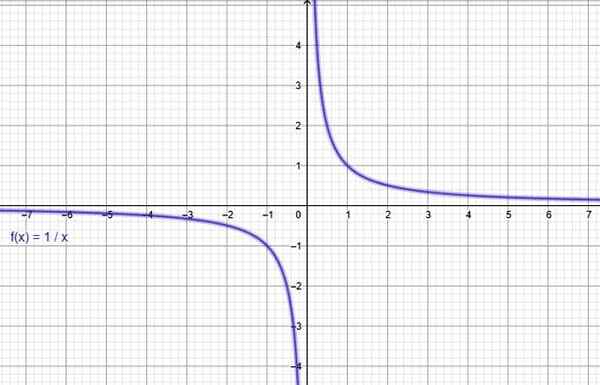De functie y = 1/x. Bron: f. Zapata door Geogebra.

Ii) omgekeerde evenredigheidsfunctie

Het is een functie van vorm:

Waarbij C een reëel getal is dan 0. Het domein is de set reële getallen behalve 0.

Je.1.c) irrationele functies

Zijn degenen wiens onafhankelijke variabele onder een radicaal teken staat. De algemene vorm is:

Sommige van deze functies kunnen zijn:

• 
• 

Het domein van deze functies wordt als volgt bepaald:

-Als de wortels van koppelindex zijn, moet de subradische hoeveelheid f (x) altijd 0 of positief zijn.

-Wanneer de wortels vreemd zijn, kan f (x) positief of negatief zijn. Daarom zijn in dit geval het domein van de functie de reële getallen.

Bijvoorbeeld het domein van:

Het is de set reële getallen zodanig dat X-3 groter is dan of gelijk is aan 0. In dit geval moet X groter zijn dan of gelijk zijn aan 3. Daarom is het domein van deze functie de set van waarden van het interval [3, ∞+).

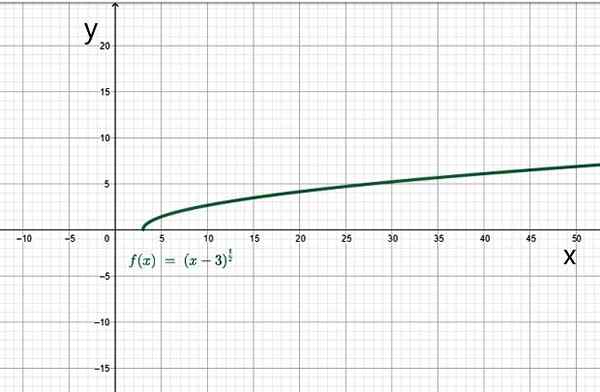 Voorbeeld van irrationele functie. Bron: f. Zapata.

Je.1.d) functioneert in stukken of door secties

De functie in delen, door secties of stukken is er een die meer dan één formule vereist voor verschillende domeinwaarden. Hier zijn enkele voorbeelden van uw toepassing:

-Tarieven voor het verzenden van pakketten per post, afhankelijk van het gewicht of volume, oorsprong en bestemming van hetzelfde.

-Tarieven voor diensten, bijvoorbeeld telefonie en elektriciteit.

-Verkoop van tickets voor musea of ​​pretparken, afhankelijk van de leeftijd.

In wiskundige vorm kan een functie in delen bijvoorbeeld zijn:

Het domein van een functie in delen hangt af van de definitie ervan. In het vorige voorbeeld is het domein de set gevormd door: (-∞, -1) ∪ [1,+∞).

De absolute waarde -functie. Bron: f. Zapata door Geogebra.

Ii) Escalonada -functie

De grafiek van deze functie door secties bestaat uit stappen, zoals die van een ladder of van verschillende hoogten kunnen zijn, afhankelijk van de manier waarop de functie is gedefinieerd.

Het kan je bedienen: Hipparco van Nicea: biografie en bijdragen aan de wetenschap

Hiervoor wordt een eindig interval [a, b] gekozen dat een bepaald eindig aantal discontinuïteiten bevat, genaamd x_Je < x₁ < x₂ <… . x_N  En er wordt een open interval gekozen (x_Je , X_I+1) Om het een constante van waarde te geven S_Je, Met de sprongen op punten x_Je. De waarde van s_Je Het is de hoogte van de stap in de stap.

Een voorbeeld van een gespreide functie is het hele deel, dat elk getal nodig heeft en het associeert met het volgende gehele getal, hetzij door overtollig of standaard. Het volgende is een volledig deel:

[x] = (groter gehele getal ≤ x)

Volgens deze functie, het hele deel van 2.5 is:

[2.5] = (groter gehele getal ≤ 2.5) = 2

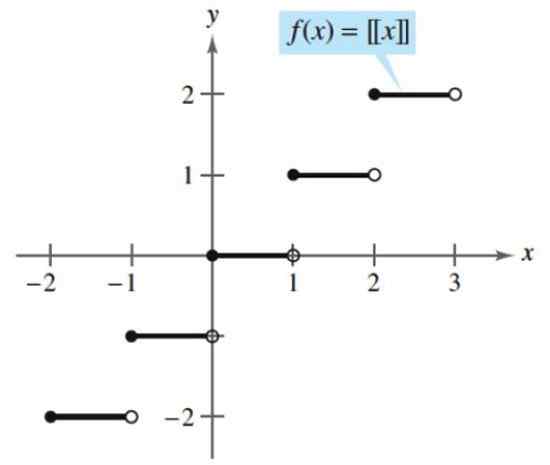Het hele deel van. Bron: Larson, r. Berekening met analytische geometrie. McGraw-Hill.

Je.2) Transcendente functies

Niet -algebraïsche functies worden transcendent genoemd. De exponentiële, logaritmische en trigonometrische functies zijn transcendente functies.

In hen de variabele X Het maakt deel uit van het argument van de functie of als onderdeel van de exponent of de index van een root, bijvoorbeeld:

• f (x) = log (x+1)
• H (x) = -0.2⋅8^-3x

Transcendente functies hebben veel toepassingen, bijvoorbeeld in de studie van trillingen en golven, waarschijnlijkheidsverdelingen, modellering van de golven, de groei van verschillende populaties, radioactief verval, rentetarieven en nog veel meer. 

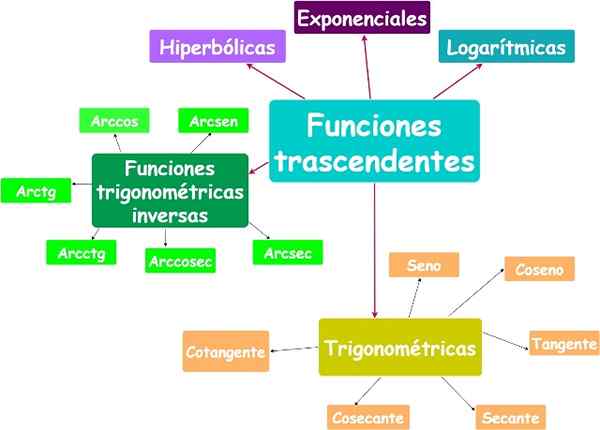Belangrijkste transcendente functies. Bron: f. Zapata.

Je.2.a) exponentiële functie 

De exponentiële functie wordt gedefinieerd door:

f (x) = a^X

Waarbij a de basis is, wat altijd een positief getal is van 1, en de variabele, een reëel getal, verschijnt in de exponent. Over het algemeen is de exponentiële functie geschreven:

f (x) = a⋅a^Bx

Hier zijn A en B echte coëfficiënten. De volgende zijn functies van dit type:

• f (x) = 5e^X
• H (x) = 4. 10^5x
• g (t) = 8e^-2t

Baseren En, waar En Het is het aantal Euler 2.71828 ... verschijnt vaak in problemen van wetenschap en engineering, evenals statistieken. Wanneer de functie heeft, wordt deze basis genoemd Natuurlijke exponentiële functie.

Het domein van de exponentiële functie is de set reële getallen, terwijl het bereik de positieve cijfers is.

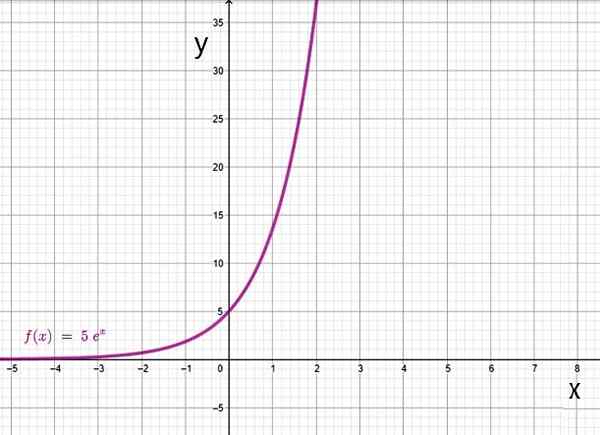Exponentiële functie op basis van. Bron: f. Zapata door Geogebra.

Je.2.b) Logaritmefunctie

Van zijn kant, de logaritm -functie gebaseerd op naar Het is de omgekeerde functie van de exponentiële functie op basis van naar. Ja:

aanroepen_naar x = y

Dus:

x = a^En

In het bijzonder, als de basis van de logaritme nummer E is, wordt de functie opgeroepen Neperian logaritm -functie En het wordt aangeduid als ln. Functies van dit type zijn:

• f (x) = ln x
• g (x) = log (x+1)
• H (t) = 1 - log x²

Het domein van de Logaritm -functie, ongeacht de basis, zijn de positieve reële getallen, exclusief de 0. Dat wil zeggen, er zijn geen logaritmen van negatieve getallen of 0.

Een logaritme kan echter 0 of negatief zijn: de logaritme van het getal tussen 0 en 1 is negatief en bereikt van zijn deel_naar 1 = 0.

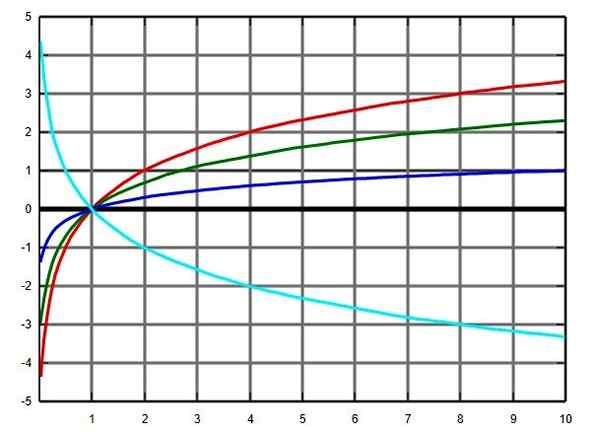Logaritm -functiegrafiek in verschillende basen: basis 2 in rood, groen E, blauwbasis en turquoise op basis 0.5. Bron: Wikimedia Commons.

Je.2.c) trigonometrische functies

Het zijn degenen die voortkomen uit de trigonometrische redenen: sinus, cosinus, raaklijn, drogen, harmoneren en cotangent van een hoek x. Ze worden respectievelijk aangeduid als:

Sen X, Cos X, Tg X, Sec X, Harm X en COTG X

Het zijn periodieke functies, wat betekent dat de vorm ervan repetitief is, dus ze zijn erg nuttig om natuurlijke fenomenen te beschrijven, zoals signalen, oscillaties, cirkelvormige beweging en swingbewegingen, die worden gekenmerkt door repetitief te zijn.

Voorbeelden van trigonometrische functies zijn:

• f (x) = sin x
• G (t) = 5⋅cos (ωt + π)
• H (x) = tg (x/2)

Variabele X wordt uitgedrukt in radianen.

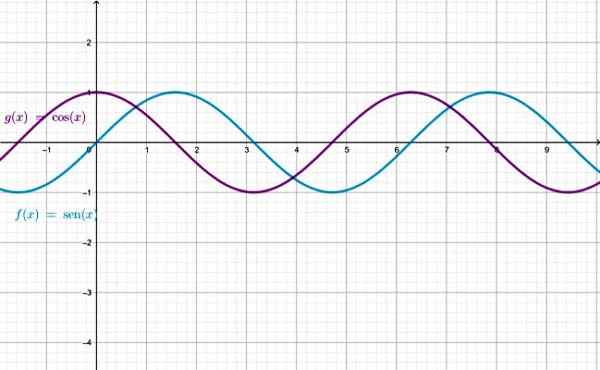Grafiek van de functies Sen X en Cos X, merk op dat ze identiek zijn, behalve dat de ene is verplaatst met betrekking tot de andere. Bron: f. Zapata door Geogebra.

De beheersing van de functies Sen X en Cos X is de set reële getallen. Voor de resterende functies zijn er X -waarden waarvoor de functie niet is gedefinieerd:

-De Tg X -functie bestaat niet wanneer x = ± π /2, ± 5π /2 ... Dit is alle oneven veelvouden van π /2.

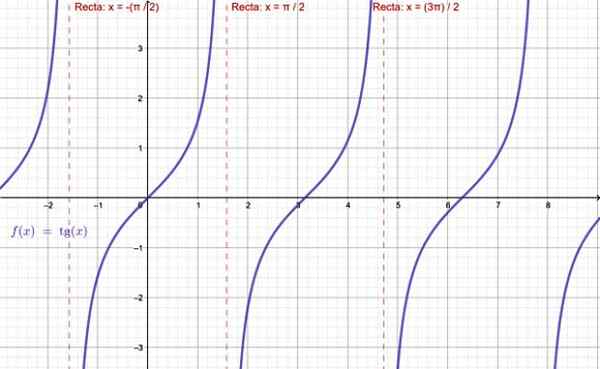Grafiek van de tangens -functie. Bron: f. Zapata door Geogebra.

-Wat f (x) = cotg x, deze functie wordt niet gedefinieerd voor de gehele veelvouden van π: ± π, ± 2π, ± 3π ..

Kan u van dienst zijn: wet van tekenen

-De Y = Sec X -functie is niet geldig wanneer cos x = 0, die x = ± π /2, ± 5π /2 ... van het domein uitsluit.

-Ten slotte behoren de gehele veelvouden van π niet voor f (x) = harm x, niet tot hun domein.

Je.2.d) Hyperbolische functies

Hyperbolische functies zijn speciale combinaties van exponentiële en^X en e^-X En ze worden genoemd als een boezem, Coseno .. .hyperbolisch. Net als bij trigonometrische functies, ook wel "circulaire" genoemd, zijn er 6 hyperbolische functies:

-Hyperbolische sinus Senh X:

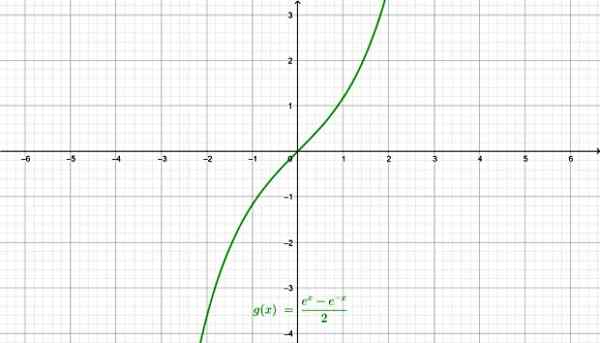De hyperbolische sinusfunctie. Bron: f. Zapata door Geogebra.

-Hyperbolische cosinus Cosh X:

 -Hyperbolische raaklijn tanh x:

 -Hyperbolische oogst CSCH X:

 -Hyperbolisch secant SECH X:

-Hyperbolisch cotangent Coth x:

Een flexibele kabel, gemaakt van uniform en hangmateriaal tussen twee punten, neemt de vorm aan van een curve genaamd katten-, die wordt uitgedrukt als een hyperbolische cosinus:

Je.2.e) Inverse trigonometrische functies

Ze komen overeen met het omgekeerde van trigonometrische functies. Wat zou bijvoorbeeld de hoek (boog) zijn waarvan de boezem 0 waard is.5?

Het antwoord is arc sen 0.5, dat luidt: “Arc sinus van 0.5 ”, en deze hoek is 30º, hoewel dit in principe niet de enige hoek zou zijn waarvan de boezem 0 waard is.5, omdat de Sen X -functie periodiek is. Wat er gebeurt, is dat als de Sen X -functie door zijn domein wordt genomen, deze niet inverse zou zijn, dus de arcoseno -functie kon niet worden gedefinieerd. Het probleem wordt opgelost door alles te beperken tot de hoeken tussen -π/2 en +π/2.

Dit kan als volgt worden uitgedrukt:

Als arc sen x = θ, betekent dit dat sin θ = x

Met -π/2 ≤ θ ≤ π/2.

Een andere notatie die wordt gebruikt voor boog sen x is f (x) = sin^-1 X. De grafiek wordt hieronder weergegeven:

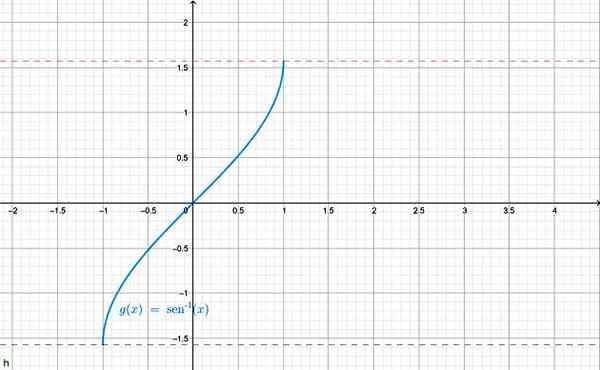Arcsen X -functie Graphics. Bron: f. Zapata door Geogebra.

Het is ook mogelijk om inverse te definiëren voor de andere trigonometrische functies, bijvoorbeeld: boog cos x = θ en dus. Voor elke rang is de rang op de juiste manier beperkt, om de omgekeerde van de overeenkomstige trigonometrische functie te zijn.

Ii) functioneert volgens zijn symmetrie

II.1) Par

Als voor alle x die tot het domein van f (x) hoort, wordt vervuld dat:

f (x) = f (-x)

Er wordt gezegd dat de functie zelfs is, zoals die volgen:

• f (x) = x² - 3
• g (x) = cos x
• 

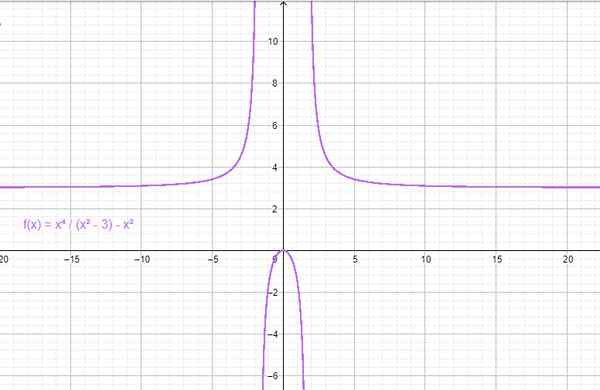  Voorbeeld van een paarfunctie. Bron: f. Zapata door Geogebra.

Bijvoorbeeld x = 1 in f (x) = x² - 3 is verkregen:

f (1) = 1² - 3 = -2.

En als x = -1, dan:

f (-1) = (-1)² - 3 = -2.

Beide resultaten zijn identiek.

De gelijkmatige functies hebben symmetrie rond de verticale as, zoals te zien is in de vorige figuur.

II.2) vreemde functie

Aan de andere kant, ja:

f (-x) = -f (x)

De functie is vreemd.

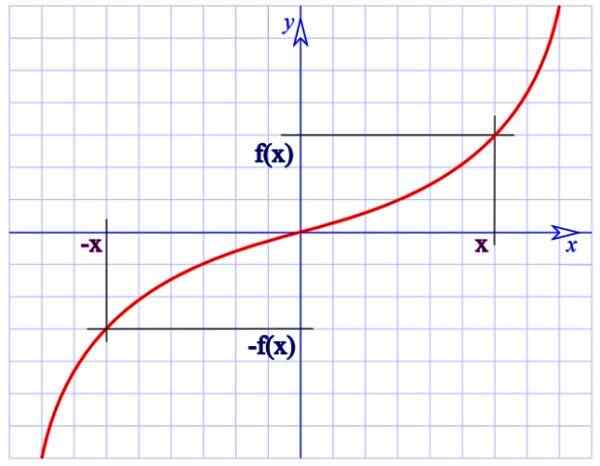Een vreemde functie. Bron: Wikimedia Commons.

De functie f (x) = 1/x van de bovenste figuur is bijvoorbeeld vreemd, omdat:

f (-x) = -1/x

EN

-f (x) = -1/x

Een andere belangrijke imparfunctie is f (x) = sin x.

Merk op dat oneven functies 180º rotatiesymmetrie hebben rond de oorsprong (de grafiek is niet gewijzigd als elk punt ervan 180º wordt gedraaid ten opzichte van de oorsprong van coördinaten).

Iii) functie volgens de expressie van de variabele

III.1) Expliciete functies

Ze worden direct uitgedrukt in termen van de afhankelijke variabele zoals y = f (x). Bijvoorbeeld:

• f (x) = x³

III.2) Impliciete functies

In impliciete functies lijkt geen van de variabelen duidelijk. Ze worden uitgedrukt als f (x, y) = 0, zoals:

• X² + En² -3xy = 0
• xy = - x²+ X-5

De functies die in dit artikel worden beschreven, zijn expliciete functies.

Iv) Functies volgens uw afbeeldingen

Volgens hun grafiek kunnen de functies continu of discontinu zijn. Continue functies kunnen worden getraceerd zonder de slag te onderbreken, aan de andere kant, discontinue functies presenteren sprongen. In de volgende afbeelding is de functie discontinu op x = a:

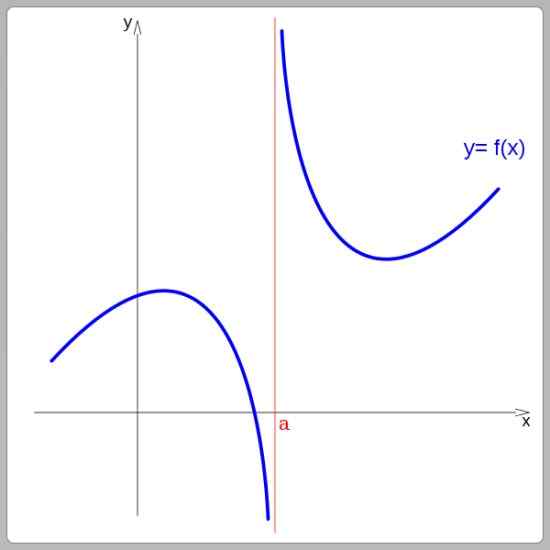Discontinuïteit functie bij x = a. Bron: Wikimedia Commons.

Voorbeelden van continue functies zijn lineaire functie, kwadratische functie en sinus- en cosinusfuncties. En onder discontinue functies zijn de gespreide functie en de tangens -functie.

V) functioneert volgens de relatie tussen de elementen van het domein en het bereik

V.1) Injectieffunctie

Een functie is Injectief Wanneer er geen twee verschillende elementen zijn in de start- of domeinset, die dezelfde afbeelding hebben in de aankomstset.

Stel dat echte functies hebben, tenzij anders aangegeven, bijvoorbeeld:

f (x) = 5x -2

Alle X -waarde die behoort tot het domein van F (x), dat de set is van de reële getallen, heeft een uniek, ook echt beeld. Aan de andere kant, in deze andere functie:

g (x) = x²

Er zijn verschillende elementen in het domein die hetzelfde beeld hebben, bijvoorbeeld x₁= 2 en x₂= -2:

G (2) = g (-2) = 4.

De manier om een ​​injectieffunctie uit de grafiek te identificeren, is een horizontale lijn trekken, als deze op meer dan één punt naar de curve wordt gesneden, is de functie niet -injectief.

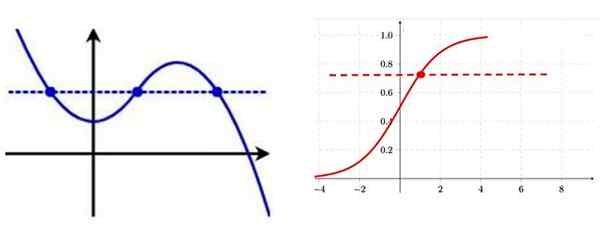Links een VN -injectieffunctie, merk op dat er verschillende punten van de grafiek zijn met dezelfde verticale coördinaat. Aan de rechterkant een injectieffunctie, op elk van de punten van de curve heeft het een bepaalde "y" -coördinaat. Bron: f. Zapata.

V.2) Overjectieffunctie

In de Onjectieve functies, Alle elementen van de aankomstset zijn afbeelding van een element van de startset. Een voorbeeld van overjectieffunctie is dezelfde f (x) = 5x -2, maar g (x) = x² Dat is het niet, omdat de genomen waarden g (x) slechts de positieve reële zijn en de 0.

Het domein kan echter opnieuw worden gedefinieerd zodat G (X) overjectief was, als het bijvoorbeeld verandert in alle positieve reële plus 0. 

V.3) Bijectieve functie

Ten slotte wordt een functie die zowel injectief als overjectief is, wordt genoemd Bijectief. Voorbeelden van bijectieve functies zijn: de gerelateerde functie, de exponentiële functie en de logaritm -functie.

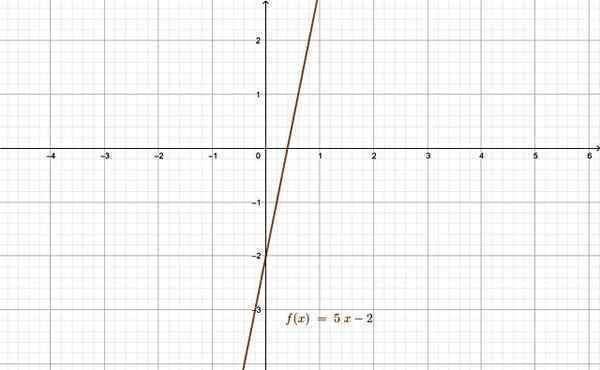De gerelateerde functie is een goed voorbeeld van bijjectieffunctie. Bron: f. Zapata door Geogebra.

Referenties

1. E-math zone. Soorten functies. Hersteld van: Emathzone.com.
2. Hoffman, J.G. Selectie van wiskundeproblemen. ED. SPPHINX.
3. Wiskunde is leuk. Commons functioneert referentie. Hersteld van: Mathisfun.com.
4. Eisen, b. Universe -formules. Soorten functies. Hersteld van: UniversOFormulas.com.
5. Stewart, J. 2006. Precculment: wiskunde voor berekening. 5e. Editie. Cengage leren.