Torricelli stelling

Wat is de stelling van Torricelli?

Hij Torricelli stelling o Torricelli -principe stelt dat de snelheid van de vloeistof die door het gat in de wand van een tank of container uitkomt, identiek is waaraan een object verwerft dat vrij wordt gevallen door een hoogte gelijk aan die van het vrije oppervlak van de vloeistof tot Het gat.

De stelling wordt geïllustreerd in de volgende figuur:

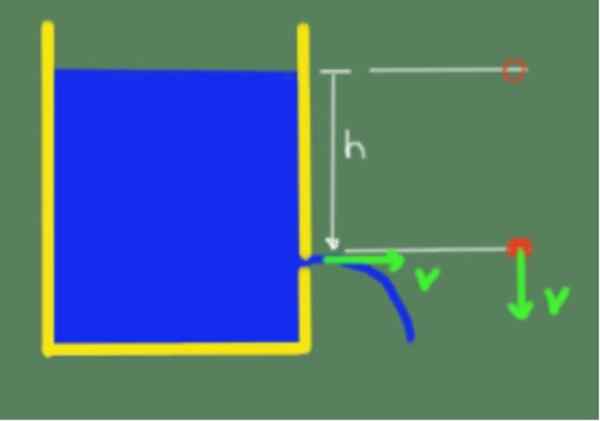Illustratie van de stelling van Torricelli. Bron: zelf gemaakt.

Vanwege de stelling van Torricelli kunnen we dan zeggen dat de snelheid van de output van de vloeistof door een gat tot hoogte h onder het vrije oppervlak van de vloeistof wordt gegeven door de volgende formule:

Waarbij g de versnelling van de zwaartekracht is en H is de hoogte van het gat tot het vrije oppervlak van de vloeistof.

Evangelist Torricelli was een lichaamsbouw en wiskundige geboren in de stad Faenza, Italië in 1608. Torricelli wordt toegeschreven aan de uitvinding van de kwikbarometer en als erkenning is er een drukeenheid genaamd "Torr", gelijkwaardig aan een kwikmillimeter (mm Hg).

Demonstratie van de stelling

In de stelling van Torricelli en in de formule die de snelheid geeft, gaat het ervan uit dat de verliezen als gevolg van viscositeit verachtelijk zijn, omdat in de vrije val wordt aangenomen dat de wrijving door de lucht die het object omringt, onbeduidend is.

De vorige veronderstelling is in de meeste gevallen redelijk en impliceert ook het behoud van mechanische energie.

Om de stelling te demonstreren, zullen we in de eerste plaats de snelheidsformule vinden voor een object dat wordt vrijgegeven met nul initiële snelheid, van dezelfde hoogte als het vloeibare oppervlak in de tank.

Kan u van dienst zijn: drie -dimensionale golven: concept, typen en voorbeelden

Het principe van het behoud van energie zal worden toegepast om de snelheid van het object te verkrijgen dat valt net wanneer een hoogte is gedaald H gelijk aan die van het gat naar het vrije oppervlak.

Aangezien er geen wrijvingsverliezen zijn, is het geldig om het principe van mechanische energiebesparing toe te passen. Stel dat het object dat valt massa M heeft en de hoogte h wordt gemeten vanaf het niveau van vloeistofuitgang.

Object dat valt

Wanneer het object wordt vrijgegeven uit een hoogte die gelijk is aan die van het vrije oppervlak van de vloeistof, is de energie alleen maar zwaartekracht, omdat de snelheid nul is en daarom de kinetische energie is nul. De potentiële energie -EP wordt gegeven door:

EP = M G H

Wanneer het voor het gat gaat, is de hoogte nul, dan is de potentiële energie nul, dus het heeft alleen kinetische energie EC gegeven door:

EC = ½ m V²

Omdat de energie wordt bewaard EP = EC van wat wordt verkregen:

½ m V² = M G H

De snelheid vrijmaken v De Torricelli -formule wordt vervolgens verkregen:

Vloeistof die uit het gat komt

Vervolgens zullen we de snelheid van de output van de vloeistof door het gat vinden, om aan te tonen dat het samenvalt met degene die net is berekend voor een object dat vrij daalt.

Hiervoor zullen we vertrouwen op het Bernoulli -principe, dat niets meer is dan het behoud van energie die op vloeistoffen wordt toegepast.

Het principe van Bernoulli is zo geformuleerd:

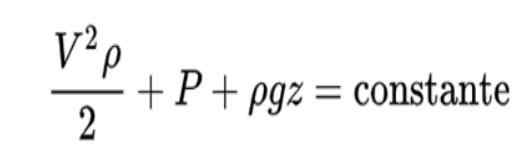
De interpretatie van deze formule is als volgt:

• De eerste term vertegenwoordigt de kinetische energie van de vloeistof per volume -eenheid
• De tweede vertegenwoordigt het werk dat wordt uitgevoerd door de druk per eenheid van dwarsgebied
• De derde vertegenwoordigt zwaartekracht potentiële energie per eenheid vloeistofvolume.

Kan u van dienst zijn: onmiddellijke snelheid: definitie, formule, berekening en oefeningen

Naarmate we beginnen met het uitgangspunt dat een ideale vloeistof is, in niet -turbulente omstandigheden met relatief lage snelheden, is het relevant om te bevestigen dat mechanische energie per volume -eenheid in de vloeistof constant is in alle gebieden of transversale secties van hetzelfde.

In deze formule V is de snelheid van de vloeistof, ρ Vloeistofdichtheid, P de druk en Z De verticale positie.

In de figuur die hieronder verschijnt, wordt de formule van Torricelli aangetoond op basis van het Bernoulli -principe.

We passen de Bernoulli -formule toe op het vrije oppervlak van de vloeistof die we aangeven (1) en in het uitgangsgat dat we aangeven door (2). Het nulhoogte -niveau is gekozen met het uitgangsgat.

In het uitgangspunt dat de dwarsdoorsnede in (1) veel groter is dan in (2), kunnen we vervolgens aannemen dat de snelheid van afname van vloeistof in (1) praktisch verwaarloosbaar is.

Dit is de reden waarom V is geplaatst₁= 0, de druk waaraan de vloeistof wordt onderworpen in (1) is de atmosferische druk en de hoogte gemeten uit het gat is H.

Voor de uitgangssectie (2) gaan we ervan uit dat de uitgangssnelheid V is, de druk waaraan de vloeistof aan de uitlaat ook wordt onderworpen, de atmosferische druk is en de uitgangshoogte nul is.

De waarden die overeenkomen met de secties (1) en (2) worden vervangen in de Bernoulli -formule en gelijk. Gelijkheid is geldig omdat we aannemen dat de vloeistof ideaal is en er geen viskeuze wrijvingsverliezen zijn. Zodra alle termen zijn vereenvoudigd, wordt de snelheid verkregen in het uitgangsgat.

Kan u van dienst zijn: rode dwerg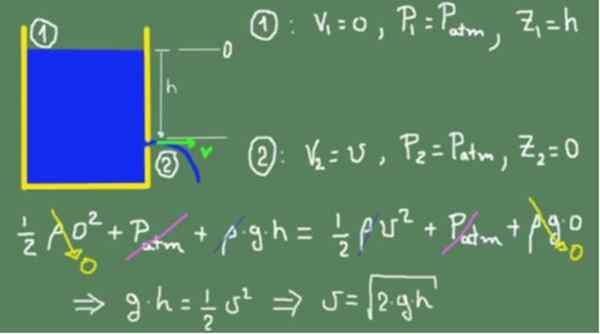

De vorige doos laat zien dat het verkregen resultaat hetzelfde is als dat van een object dat vrij valt,

Met wat wordt aangetoond het Torricelli -principe.

Opgeloste oefeningen

Oefening 1

Je) De kleine uitlaatbuis van een watertank is 3 m onder het wateroppervlak. Bereken de wateruitgangsnelheid.

Oplossing:

De volgende figuur laat zien hoe de formule van Torricelli op deze zaak wordt toegepast.

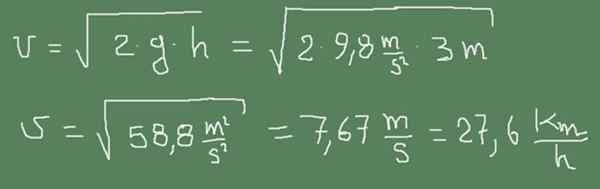
Oefening 2

II) Ervan uitgaande dat de uitgangsbuis van de vorige trainingstank een diameter van 1 cm heeft, bereken de stroom van de wateruitlaat.

Oplossing:

De stroom is het volume vloeistof dat per tijdseenheid uitkomt en wordt eenvoudig berekend door het outputgatgebied te vermenigvuldigen met de uitgangssnelheid.

De volgende afbeelding toont de details van de berekening.

Oefening 3

III) Bepaal hoe hoogte het vrije oppervlak van het water in een container is als bekend

dat in een gat aan de onderkant van de container het water op 10 m/s komt.

Oplossing:

Zelfs wanneer het gat zich onderaan de container bevindt, kan de formule van Torricelli worden toegepast.

De volgende afbeelding toont het detail van de berekeningen.

Referenties

1. Wikipedia. Torricelli stelling.
2. Hewitt, p. Conceptuele fysieke wetenschap. VIJFDE EDITIE.119.
3. Jong, Hugh. 2016. Sears-Zansky's University Physics with Modern Physics. 14e ed. Pearson. 384.