Miletus zo'n stelling

We leggen de eerste en tweede stelling van dergelijke uit, met voorbeelden en oefeningen opgelost

Figuur 1.- De verhalen over

Wat is er?

Hij Zo'n stelling Van Miletus verwijst hij eigenlijk naar verschillende geometrie -stellingen die zijn toegeschreven aan de wijze van oude Griekenland Thales van Miletus, die leefden van 624 tot 546 AC in Miletus, huidige Turkije.

Naast wiskundige en geometer was dat een filosoof die werd erkend voor zijn grote scherpte. Er wordt gezegd dat hij erin is geslaagd om de hoogte van de grote piramide te meten door het gebruik van een van zijn stellingen.

Hij Eerste stelling van dit Het verwijst naar de segmenten dat een groep parallelle lijnen in twee lijnen in het vlak bepaalt. Deze segmenten behouden een verhouding van evenredigheid, zoals binnenkort zal worden gezien, die wordt uitgebreid tot de zijkanten van twee driehoeken, op voorwaarde dat aan bepaalde voorwaarden wordt voldaan.

Deze stelling is in de praktijk uiterst nuttig, omdat het mogelijk maakt om de hoogte van zeer hoge of moeilijk toegang tot structuren te bepalen, zonder dat ze rechtstreeks moeten worden gemeten. Dit was precies wat verhalen deden toen hij de hoogte van de grote piramide gemeten.

Van zijn kant, de Tweede stelling hiervan Linkpunten die tot een omtrek behoren met een rechthoekige driehoek die erin is geregistreerd, waarvan de hypotenusa samenvalt met zijn diameter.

Eerste stelling van dit

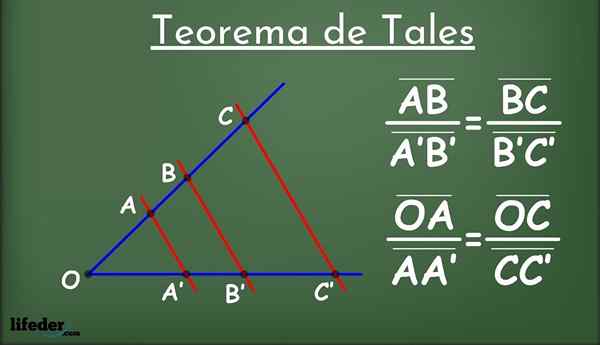
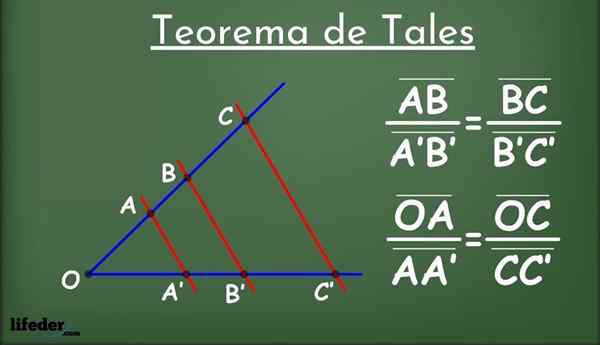
Wees twee lijnen in een vlak, L genoemd₁ en ik₂ (in blauw in figuur 1) en een groep lijnen parallel aan elkaar (in rood) die lrent l₁ en ik₂.

De parallelle lijnen verdelen de lijnen in segmenten L₁ en ik₂: Ab, a'b ', bc, b'c' enzovoort. Onder de geconfronteerde segmenten wordt de volgende evenredigheidsrelatie tot stand gebracht:

In deze figuur wordt bijvoorbeeld de maat van het "x" -segment berekend door de stelling van dergelijke, omdat de lijnen worden doorsneden door verschillende parallellen die segmenten met bekende lengte bepalen:

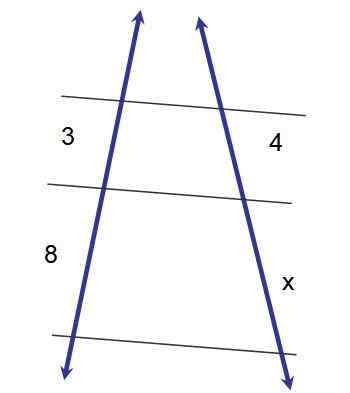Het kan u van dienst zijn: wederzijds exclusieve gebeurtenissen: eigenschappen en voorbeeldenFiguur 2.- Toepassing van de eerste dergelijke stelling om de maat van segment X te bepalen. Bron: f. Zapata.

3x = 32

x = 32/3 ≈ 10.7

De dergelijke stelling voor soortgelijke driehoeken

De stelling kan als volgt worden uitgebreid naar de driehoeken: Stel dat er een ABC -driehoek is waarop een parallel segment wordt aangetrokken tot een van de zijkanten. Op deze manier worden twee vergelijkbare driehoeken verkregen: ABC en Dec, wiens interne hoeken congruent zijn, dat wil zeggen dat ze gelijke maatregel hebben.

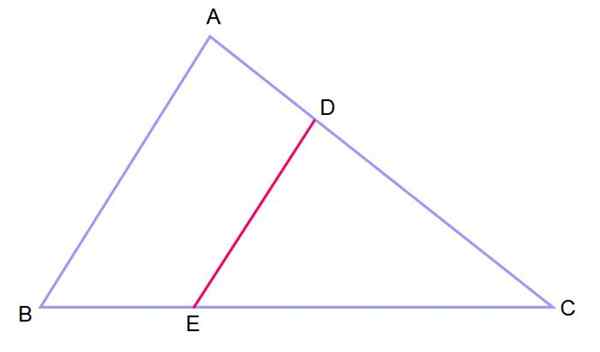figuur 3.- Twee driehoeken in de positie van dergelijke, met twee parallelle zijden en een gemeenschappelijke hoek, zijn vergelijkbaar. Bron: f. Zapata.

Als je twee driehoeken op deze manier hebt gerangschikt, wordt gezegd dat ze in zo'n positie zijn.

Een verhouding van evenredigheid tussen de segmenten wordt op dezelfde manier verhoogd als voor de parallelle lijnen:

Die gelijkwaardig is aan deze ander, tussen de overeenkomstige zijden van elke driehoek, ook wel homologe zijden genoemd:

Elk van deze quotiënten wordt genoemd gelijkenis reden. In vergelijkbare driehoeken is de reden voor gelijkenis gelijk aan het quotiënt tussen de perimeters en het kwadraat van de overeenkomstverhouding is gelijk aan het quotiënt tussen de gebieden.

Vervolgens een voorbeeld waarin de stelling kan worden toegepast op soortgelijke driehoeken en erachter komt hoeveel de onbekende kant X waard is.

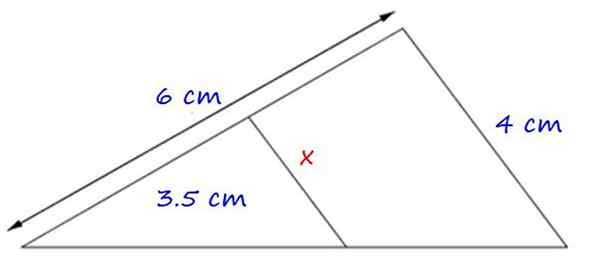Figuur 4.- Toepassingsvoorbeeld van de eerste dergelijke stelling. Bron: f. Zapata.

De gevormde driehoeken zijn vergelijkbaar, omdat ze een gemeenschappelijke invalshoek hebben en de zijkanten x en 4 cm parallel zijn.

Daarom is de evenredigheid tussen de overeenkomstige zijden:

En de waarde van X is gemakkelijk gewist:

x = (4 × 3.5) ÷ 6 cm = 2.3 cm

Tweede stelling hiervan

Deze stelling verwijst naar een driehoek waarvan de hoekpunten zijn die tot een omtrek behoren, wat betekent dat deze erin is geregistreerd.

In dit geval stelt de stelling vast dat wanneer de hypotenusa overeenkomt met de diameter van de omtrek, de aldus getraceerde driehoek rechthoek is, dat wil zeggen een van de interne hoeken meet 90º, zoals te zien in figuur 5 aan de linkerkant.

Kan u van dienst zijn: symbolisatie van uitdrukkingen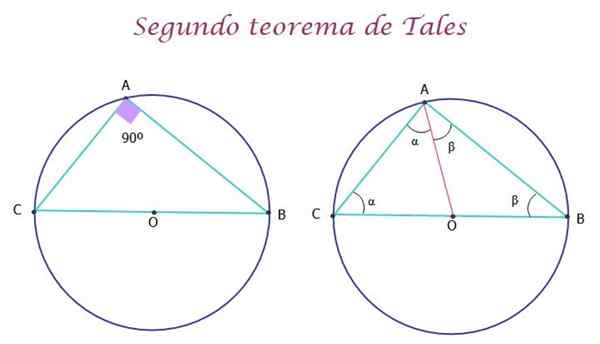Figuur 5.- De tweede stelling van dergelijke stelt dat de in de omtrek geregistreerde driehoek rechthoek is. Bron: f. Zapata.

Demonstratie van de tweede stelling van dergelijke

De demonstratie van de stelling is heel eenvoudig. In de bovenstaande figuur is het AO -segment in rood getekend om de twee AOC- en AOB -driehoeken te vormen, die gelijkbenig zijn, omdat de zijkanten OA, OC en OB radio's van de omtrek zijn en daarom meten ze hetzelfde.

Op deze manier hebben de driehoeken twee gelijke hoeken, die respectievelijk α en β zijn. Nu, voor de oorspronkelijke ABC -driehoek, zoals voor elke driehoek, is het vervuld dat de som van de metingen van de interne hoeken gelijk is aan 180º, daarom:

α + (α + β) + β = 180º

Vandaar:

2α + 2β = 180º

Daarom:

2 (α +β) = 180º

α +β = 90º

Wat bewijst dat de ABC -driehoek een interne hoek van 90º heeft en daarom een ​​rechte driehoek is.

Voorbeeld

In de volgende figuur is de driehoek ABC gelijkbenig en rechthoek (isorectangle driehoek), de omtrek van de omtrek gelijk aan 25 cm. Hoeveel zijn de AC- en AB -segmenten?

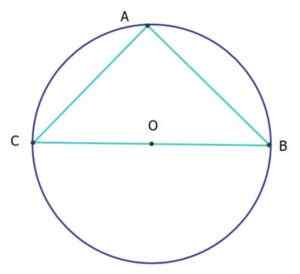
De omtrek van de omtrek is de lengte L, gegeven afhankelijk van de diameter D door formule:

L = πd

Daarom meet de diameter, die het CB -segment is,:

D = cb = l/ π = 25 cm/ π = 7.96 cm.

Omdat de driehoek gelijkbenig is, betekent dit dat de acute hoeken elk 45º meet. Aangezien de hypotenusa van de driehoek de diameter van de omtrek is, kan een trigonometrische verhouding van 45 bijvoorbeeld worden gebruikt:

Sen 45º = AC/CB

AC = CB × SIN 45º = 7.96 cm × sin 45º = 5.64 cm

Kan u van dienst zijn: Moivre Stelling

De AB -zijde heeft dezelfde maatregel: 5.64 cm, omdat de driehoek gelijkbenig is.

Dergelijke stellingstoepassingen

De eerste dergelijke stelling kan worden gebruikt om afstanden te kennen die niet gemakkelijk meetbaar zijn. Er wordt gezegd dat dergelijke reisde naar Egypte en daar op een zeer ingenieuze manier de hoogte van de grote piramide heeft bepaald.

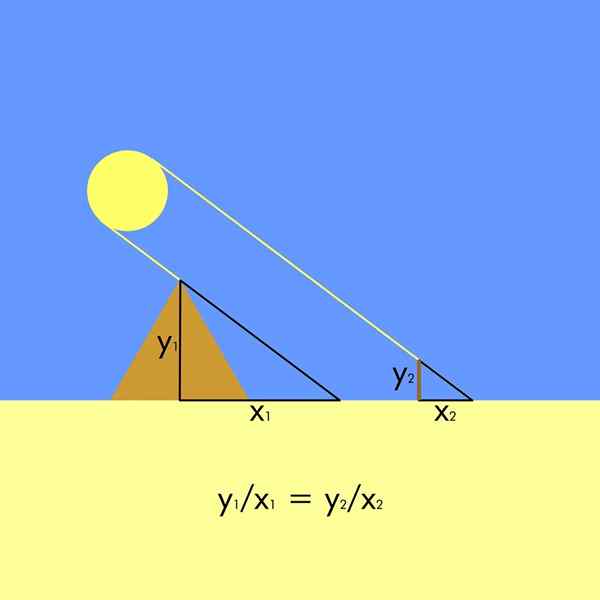
Hiervoor was het nodig. Daarom worden twee vergelijkbare driehoeken gevormd, omdat de stralen van de zon parallelle incidentie hebben.

In de figuur is de hoogte van de piramide en₁ En zijn schaduw is x₁, Terwijl de hoogte van de paal is en₂ (Sommige chroniqueurs beweren dat dit hun eigen hoogte heeft gebruikt) en hun schaduw is x₂. Omdat de driehoeken vergelijkbaar zijn, wordt de volgende evenredigheidsrelatie gevormd:

Heel gemakkelijk zijn om de hoogte van de piramide te wissen en₁:

En₁ = x₁∙ (en₂ ÷ x₂))

Referenties

1. Alexander, D. 2013. Geometrie. 5e. Editie. Cengage leren.
2. Eisen, b. Zo'n stelling. Hersteld van: UniversOFormulas.com.
3. Wiskundige hal. Tales de Mileto en de grote piramide. Opgehaald uit: Salonmatematic.com
4. Superprof didactisch materiaal. Miletus zoals. Hersteld van: superprof.is.
5. Thales en gelijkenis stelling. Twee zeer oude problemen. Hersteld van: edu.Xunta.Meid.