Kwadratische voorbeelden van opvolgingen, regel en oefeningen opgelost

De Kwadratische opvolgingen, In wiskundige termen bestaan ​​ze uit sequenties van getallen die een bepaalde rekenregel volgen. Het is interessant om deze regel te kennen om een ​​van de voorwaarden van een opvolging te bepalen.

Een manier om dit te bereiken is om het verschil tussen twee opeenvolgende termen te bepalen en te kijken of de verkregen waarde altijd wordt herhaald. Wanneer dat zo wordt gezegd dat het een regelmatige opvolging.

Numerieke opvolgingen zijn een manier om getallensequenties te organiseren. Bron: Pixabay.com

Maar als het niet wordt herhaald, kunt u proberen de Verschil tussen verschillen En kijk of deze waarde constant is. Zo ja, dan is het een Kwadratische opvolging. 

[TOC]

Voorbeelden van reguliere opvolgingen en kwadratische opvolgingen

De volgende voorbeelden helpen verduidelijken wat tot nu toe is uitgelegd:

Voorbeeld van regelmatige opvolging

Wees de opvolging S = 4, 7, 10, 13, 16, ...

Deze opvolging, aangeduid door S, is een oneindige numerieke set, in dit geval van hele getallen.

Het is te zien dat het een regelmatige opvolging is, omdat elke term wordt verkregen door 3 toe te voegen aan de vorige term of element:

4

4 +3 = 7

7+3 = 10

10+3 = 13

13+3 = 16

Met andere woorden: deze opvolging is regelmatig omdat het verschil tussen de volgende term en de vorige een vaste waarde geeft. In het voorbeeld gegeven is deze waarde 3.

De reguliere opvolgingen die zijn verkregen door een vast bedrag toe te voegen aan de vorige termijn, worden ook genoemd rekenkundige progressies. En tot het verschil - constant - onder opeenvolgende termen wordt het genoemd reden En het wordt aangeduid als r.

Voorbeeld van niet -reguliere en kwadratische opvolging

Zie nu de volgende opvolging:

S = 2, 6, 12, 20, 30, .. .

Wanneer de opeenvolgende verschillen worden berekend, worden de volgende waarden verkregen:

Kan u van dienst zijn: willekeurige selecties met of zonder vervanging

6-2 = 4

12-6 = 6

20-12 = 8

30-20 = 10

Hun verschillen zijn niet constant, dus het kan worden gezegd dat het een niet -regelmatige opeenvolging is.

Als we echter rekening houden met de reeks verschillen, is er nog een opeenvolging, die zal worden aangeduid als S_Dif:

S_Dif = 4, 6, 8, 10, .. .

Deze nieuwe opvolging is een regelmatige opvolging, Aangezien elke term wordt verkregen door de vaste waarde R = 2 toe te voegen aan de vorige. Daarom kunnen we bevestigen dat S is Kwadratische opvolging.

Algemene regel om een ​​kwadratische opvolging op te bouwen

Er is een algemene formule om een ​​kwadratische opvolging te bouwen:

T_N = A ∙ n² + B ∙ n +c

In deze formule, T_N Het is de term van de n van de opvolging. A, B en C zijn vaste waarden, terwijl N één voor één varieert, dat wil zeggen 1, 2, 3, 4, ..

Indienst van het vorige voorbeeld a = 1, b = 1 en c = 0. Van daaruit volgt dat de formule die alle voorwaarden genereert, is: T_N = n² + N

Het is te zeggen:

T₁ = 1² + 1 = 2

T₂ = 2² + 2 = 6

T₃ = 3² + 3 = 12

T₅ = 5² + 5 = 30

T_N = n² + N

Verschil tussen twee opeenvolgende termen van een kwadratische opvolging

T_N+1 - T_N = [A ∙ (n+1)² + B ∙ (n + 1) + c] - [a ∙ n n² + B ∙ n +c]

Het ontwikkelen van de uitdrukking door opmerkelijk product blijft bestaan:

T_N+1 - T_N = A ∙ n² + A ∙ 2 ∙ n + a + b ∙ n + b + c - a ∙ n n² - B ∙ n - c

Door het te vereenvoudigen, krijg je:

T_N+1 - T_N = 2 ∙ a ∙ n + a + b

Dit is de formule die de opeenvolging van de verschillen geeft_Dif dat kan zo worden geschreven:

Dif_N = A ∙ (2n+1)+B

Waar duidelijk de volgende term 2 ∙ soms de vorige is. Dat wil zeggen de reden voor de opeenvolging van de verschillen s_Dif Es: r = 2 ∙ a.

Opgeloste oefeningen van kwadratische opvolgingen

Oefening 1

Wees de opvolging S = 1, 3, 7, 13, 21,…. Bepaal ja:

i) het is regelmatig of niet

ii) is kwadratisch of niet

iii) was kwadratisch, de opeenvolging van verschillen en hun reden

Het kan u van dienst zijn: Limiet Eigenschappen (met voorbeelden)

Antwoorden

i) Laten we het verschil berekenen de volgende term en het vorige:

3-1 = 2

7-3 = 4

13-7 = 6

21-13 = 8

We kunnen bevestigen dat successie S niet regelmatig is, omdat het verschil tussen opeenvolgende termen niet constant is.

ii) De opeenvolging van de verschillen is regelmatig, omdat het verschil tussen de termen ervan de constante waarde is 2. Daarom is de oorspronkelijke opvolging S kwadratisch.

iii) We hebben al vastgesteld dat S kwadratisch is, de opeenvolging van de verschillen is:

S_Dif = 2, 4, 6, 8,… en de reden is r = 2.

Oefening 2

Wees de opvolging S = 1, 3, 7, 13, 21, ... van het vorige voorbeeld, waar het werd geverifieerd dat het kwadratisch is. Bepalen:

i) de formule die de algemene term T bepaalt_{N .}

ii) verifieer de derde en vijfde termijn.

iii) de waarde van de tiende termijn.

Antwoorden

i) de algemene formule van t_N is een ∙ n² + B ∙ n +c. Dan is het bekend de waarden van A, B en C.

De opeenvolging van verschillen is goed 2. Naast een kwadratische opvolging is de reden dat R 2 ∙ A is zoals aangetoond in de vorige secties.

R = 2 ∙ a = 2 waardoor we concluderen dat a = 1.

De eerste term van de opeenvolging van verschillen s_Dif Het is 2 en moet voldoen aan ∙ (2n+1)+b, met n = 1 en a = 1, dat wil zeggen:

2 = 1 ∙ (2 ∙ 1+1)+B

Clearing B wordt verkregen: B = -1

Dan de eerste term van S (n = 1) Vale 1, dat wil zeggen: 1 = a ∙ 1² + B ∙ 1 + C. Omdat we al weten dat a = 1 en b = -1, ons vervangen, zijn we over:

1 = 1 ∙ 1² + (-1) ∙ 1 +c

Het wissen van C wordt verkregen de waarde ervan: C = 1.

Samengevat:

A = 1, B = -1 en C = 1

Dan is de term gewoon_N = n² - N + 1

ii) de derde term t₃ = 3² - 3 + 1 = 7 en is geverifieerd. De vijfde T₅ = 5² - 5 + 1 = 21 dat is ook geverifieerd.

iii) de tiende term zal zijn₁₀ = 10² - 10 + 1 = 91.

Oefening 3

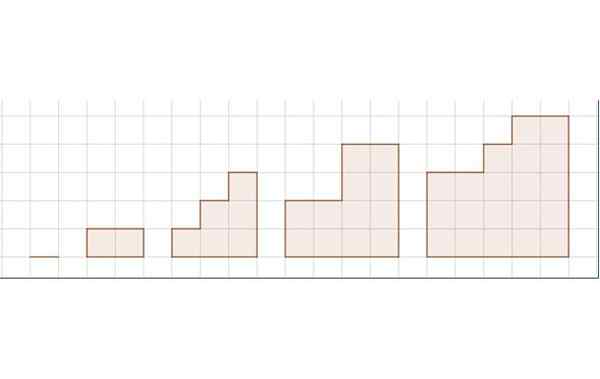Volgorde van gebieden voor oefening 3. Bron: zelf gemaakt.

De figuur toont een reeks van vijf figuren. Het reticulaire vertegenwoordigt de lengte -eenheid.

Kan u van dienst zijn: verschil tussen een gemeenschappelijke fractie en een decimaal aantal

i) Bepaal de opvolging voor het gebied van het cijfers.

i) Laat zien dat het een kwadratische opvolging is.

iii) Vind het gebied van figuur # 10 (niet getoond).

Antwoorden

i) De opvolging van het gebied van de reeks figuren is:

S = 0, 2, 6, 12, 20,…

ii) De opvolging die overeenkomt met de opeenvolgende verschillen van de voorwaarden van S is:

S_Dif = 2, 4, 6, 8,…

Omdat de verschillen tussen opeenvolgende termen niet constant zijn, is S dus geen regelmatige opeenvolging. Het moet weten of het kwadratisch is, waarvoor we opnieuw de volgorde van de verschillen maken, het verkrijgen:

2, 2, 2, .. .

Omdat alle termen van de reeks worden herhaald, wordt bevestigd dat S een kwadratische opvolging is.

iii) Successie s_Dif is regelmatig en zijn reden R is 2. Met behulp van de eerder aangetoonde vergelijking r = 2 ∙ A, blijft:

2 = 2 ∙ a, wat impliceert dat a = 1.

De tweede term van de opeenvolging van verschillen s_Dif Het is 4 en het n -em van S_Dif is

A ∙ (2n+1)+B.

De tweede term heeft n = 2. Er werd ook vastgesteld dat a = 1, dus het gebruik van de vorige vergelijking en het vervangen ervan is:

4 = 1 ∙ (2 ∙ 2+1)+B

Clearing B wordt verkregen: B = -1.

Het is bekend dat de tweede term van S 2 waard is en dat de formule van de algemene term moet vervullen met n = 2:

T_N = A ∙ n² + B ∙ N +C; n = 2; A = 1; B = -1; T₂ = 2

Het is te zeggen

2 = 1 ∙ 2² - 1 ∙ 2 + c

Er wordt geconcludeerd dat C = 0, dat wil zeggen dat de formule die de algemene term van de opvolging geeft, is:

T_N = 1 ∙ n² - 1 ∙ n +0 = n² - N

Nu is de vijfde termijn geverifieerd:

T₅ = 5² - 5 = 20

iii) Figuur #10, dat hier niet is getekend, zal het gebied hebben dat overeenkomt met de tiende termijn van de S -opvolging:

T₁₀ = 10² - 10 = 90

Referenties

1. https: // www.Geogebra.borg