Wiskunde

Rechthoekig coördinatensysteem

Rechthoekig coördinatensysteem
Cartesiaans coördinatensysteem in drie dimensies. Bron: Wikimedia Commons

Wat is het rechthoekige coördinatensysteem?

In wiskunde en geometrie, een rechthoekig coördinatensysteem Het dient om precies elk punt op de ruimte te vinden. Hiervoor is het voldoende om drie coördinaten te geven.

De constructie van het systeem in het vlak is heel eenvoudig, slechts drie lijnen die de coördinaatassen of Cartesiaanse assen zijn, zijn nodig: de ene verticaal, een andere horizontaal en een derde die het papier of het scherm binnenkomt of verlaat.

Deze assen zijn onderling loodrecht en het snijpunt is de oorsprong van het systeem.

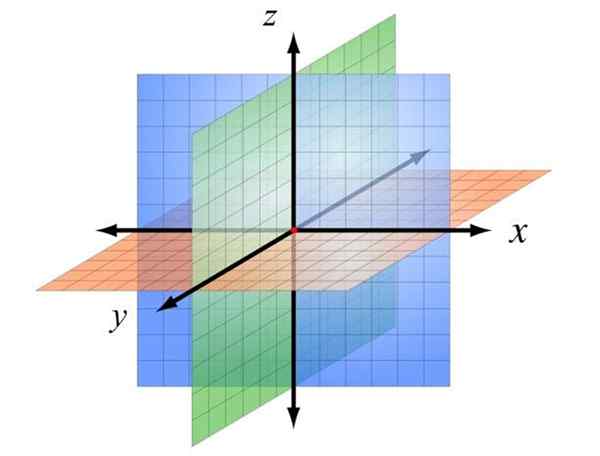
Deze bepaling wordt weergegeven in de bovenstaande figuur, waarin de letters aan de letters zijn toegewezen X, En, Z, om ze te onderscheiden. Op deze manier worden drie vliegtuigen bepaald, met de oorsprong gekleurd in rood.

Het vliegtuig XZ, In blauw is het het vlak van het scherm en staat voor de ogen van de lezer. Het vliegtuig XY Het is oranje en kan worden geassocieerd met de tafel of de vloer. Eindelijk het vliegtuig zy In het groen staat het loodrecht op de vorige en versnelt het scherm of papier in twee regio's.

Als u elk van deze vlakken quaduleert en een schaal toewijst, kunt u elk punt in de ruimte plaatsen die de respectieve coördinaten geeft X en Z, Altijd in die volgorde, om dubbelzinnigheden te voorkomen.

WaarvoorHet dient het rechthoekige coördinatensysteem?

Het rechthoekige coördinatensysteem dient om elk punt in de ruimte of in het vlak te positioneren, voldoende om de drie coördinaten van het punt aan te geven, in volgorde x, y, z.

Het kan u van dienst zijn: nominale variabele: concept en voorbeelden

Als het punt tot een vlak hoort, is een van de coördinaten 0 en als het op een van de assen is, zijn twee van de coördinaten 0, behalve dat overeenkomend met de locatie van het punt, behalve de oorsprong, die, als eerder gezegd, heeft coördinaten (0,0,0).

De volgende voorbeelden verduidelijken het bovenstaande.

Voorbeelden

voorbeeld 1

Een elk punt P op de X -as wordt uitgedrukt door coördinaten P (x, 0, 0). Merk op dat de oorsprong, in de volgende figuur rood gemarkeerd, coördinaten heeft of (0, 0, 0).

Wanneer het punt rechts van de oorsprong is, heeft het een positieve X -coördinaat, terwijl als het links is, het negatief is. P1 Blue Point heeft bijvoorbeeld coördinaten (6,0,0), terwijl punt P2 in groen, heeft coördinaten (-9,0,0).

Voorbeeld 2

In de volgende figuur zijn er twee assen, zijnde de X Axis de horizontale as en de As y Het verticaal. Hiermee is het voldoende om punten in het vliegtuig weer te geven, twee coördinaten zijn noodzakelijk. De oorsprong of is het punt (0.0).

Merk op dat de opstelling van de assen het vlak verdeelt in vier genoemde regio's kwadranten. De assen boven en rechts van de oorsprong worden aangeduid met een positief teken, terwijl ze onder en links worden onderscheiden met een negatief teken.

Vervolgens komen de punten waarvan de coördinaten positief zijn, beide, komen overeen met het eerste kwadrant of kwadrant I. Het groene punt heeft coördinaten (2,3) en zit in het i -kwadrant.

Van zijn kant heeft het rode punt coördinaten (-3,1) en bevindt zich in het II-kwadrant, terwijl de coördinaten van het blauwe punt zijn (-1.5; -2.5) en het is in het III -kwadrant.

Kan u van dienst zijn: gemeenschappelijke factorisatie: voorbeelden en oefeningen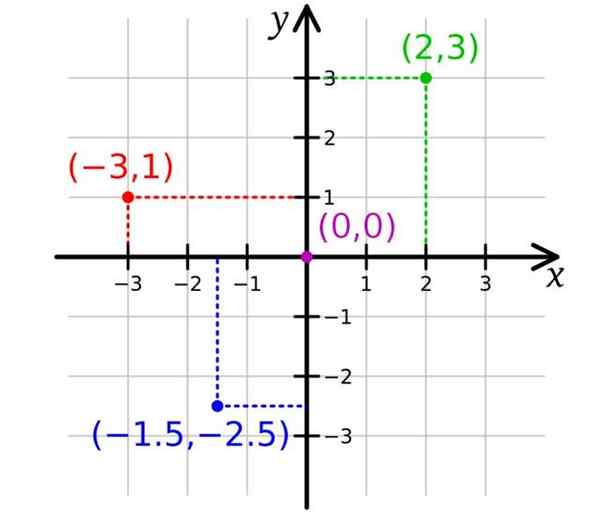 Cartesiaans vlak. Bron: Wikimedia Commons

Voorbeeld 3

Het volgende is een voorbeeld van een punt in de ruimte. De coördinaten zijn x = 6, y = 10 en z = 8, daarom, P (6,10,8).

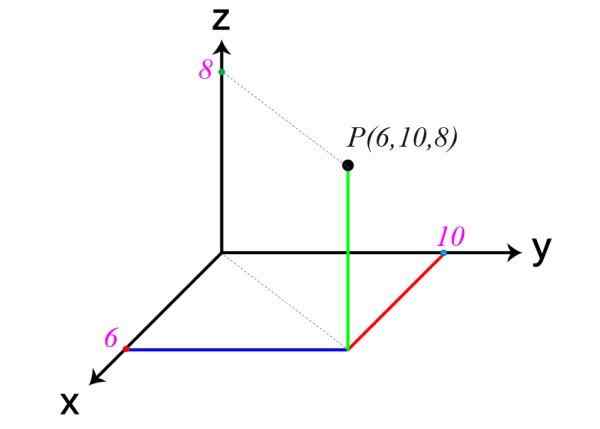Een ander voorbeeld van Cartesiaanse assen

In de figuur van het begin wordt gewaarschuwd dat de plannen XY, XZ en ZY de ruimte in acht regio's verdelen, genaamd Octavers. Punt P van het voorbeeld is in de eerste ocant.

Referenties

  1. Alexander, D. (2013). Geometrie. 5e. Editie. Cengage leren.
  2. Larson, r. (2012). Voorzetting. 8e. Editie. Cengage leren.
  3. Stewart, J. (2007). Precculment: wiskunde voor berekening. 5e. Editie. Cengage leren.
  4. Het Cartesiaanse vlak. Opgehaald van: DL.UNCW.Edu.
  5. Weisstein, E. Cartesiaanse coördinaten. Hersteld van: Mathworld.Wolfraam.com