Rechte en semi -gerelateerde segment

Een lijn van lijn en een semi -rechterkant worden onderscheiden in het feit dat het lijnsegment beperkt is; dat wil zeggen, hun eerste punt en hun eindpunt zijn bekend. Vanaf de semi -rechter is bekend zijn initiële punt, maar niet het eindpunt, omdat het zich uitstrekt tot oneindig.

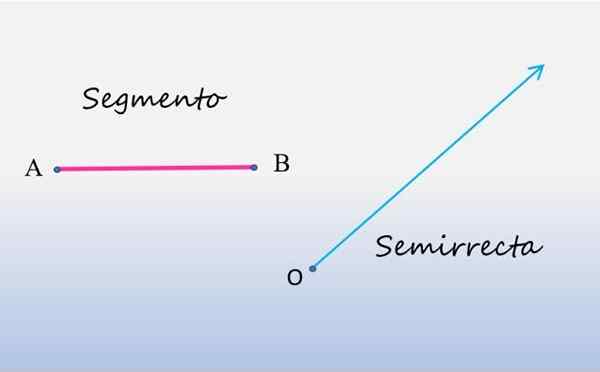
De volgende figuur toont, links, een lijnsegment, en rechts, een semi -rechter:

Segment en semi -recht. Bron: f. Zapata.

Zoals te zien is, is het segment een lijnlijnlijn, die begint op punt A en eindigt op punt B, deze punten zijn de uiteinden van het segment. De meting van het segment komt overeen met de lengte tussen de uiteinden.

Van zijn kant heeft de semi -recht zijn startpunt op het punt O en strekt zich uit tot oneindig, wat gelijk is aan te zeggen dat het slechts door één uiteinde wordt beperkt, meestal oorsprong genoemd. Om deze reden worden ze ook genoemd goeie hemel.

De segmenten worden aangegeven via de letters die het beginpunt en het einde aangeven. Het segment van de figuur is bijvoorbeeld segment AB, of een slag wordt bovenop geplaatst, zoals deze:

Aan de andere kant kan een semi -recovery ook worden benoemd met twee letters, een die het punt aangeeft dat overeenkomt met de oorsprong en nog een extra brief. Het kan ook een kleine brief worden gebruikt om de bliksem of semi -recreatie weer te geven, en er zijn ook semi -strak met zijn eigen naam, zoals later in de voorbeelden zal worden gezien.

Voorbeelden van segmenten

De segmenten zijn erg belangrijk in de geometrie, hieronder zijn enkele van de meest opvallende:

Zijkanten van een polygoon

De polygonen zijn platte en gesloten cijfers, waarvan de zijden niet -opeenvolgende lijnsegmenten zijn. Een driehoek heeft bijvoorbeeld drie zijden, een vierhoek heeft vier zijden, een Pentagon heeft er vijf enzovoort.

Het kan u van dienst zijn: Tesseldos: karakteristiek, typen (regelmatig, onregelmatig), voorbeelden

Diameter van een omtrek

Het wordt gedefinieerd als dat segment dat twee punten van de omtrek bevat en noodzakelijkerwijs door het midden van hetzelfde gaat.

Touw van een omtrek

Wanneer een segment dat twee punten van de omtrek verbindt, niet door het midden gaat, wordt het touw genoemd.

Hoogte van een driehoek

De hoogte van een driehoek wordt gedefinieerd als het segment dat loodrecht op een van de zijkanten van de driehoek naar het tegenoverliggende hoekpunt gaat. Als de maat van de basis van een driehoek, B en de hoogte van hetzelfde genoemd, aangeduid als H is bekend, wordt het gebied A van hetzelfde berekend door de goed bekende formule:

A = ½ B ∙ H

Semirret voorbeelden

Semi -straight zijn ook zeer belangrijke elementen in geometrie. Sommige goed bekende semi -straight zijn:

De positieve semi -messages

De drie richtingen in de ruimte: hoog, breed en diepte, kunnen worden weergegeven door een systeem van cartesiaanse assen, bestaande uit drie wederzijds loodrechte lijnen met elkaar, aangeduid als assen X, En En Z, die worden gesneden op een punt dat wordt genoemd oorsprong.

Deze bepaling verdeelt ruimte in acht regio's die bekend staan ​​als Octavers. In de volgende figuur worden de positieve semi -deuren waargenomen X, En En Z, die de eerste ocant bepalen. Evenzo bepaalt de positieve semi -x y y het gebied van het vliegtuig dat wordt genoemd Eerste kwadrant.

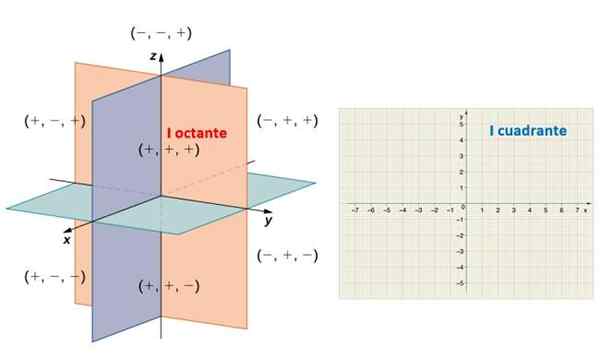Aan de linkerkant, de acht octanten van de ruimte en rechts, verdeeld het Cartesiaanse vlak verdeeld in vier kwadranten. Bron: Math Librhethexts.

De zijkanten van een hoek

Een hoek is de fractie van het vlak dat wordt afgebak. Dit in het algemeen is het de hoekpunt van de hoek, terwijl de semi -straight respectievelijk de eerste kant en de laatste kant van de hoek worden genoemd. Een dergelijke bepaling wordt in de volgende figuur getoond:

Het kan u van dienst zijn: wat is de relatie tussen het rhombusgebied en de rechthoek?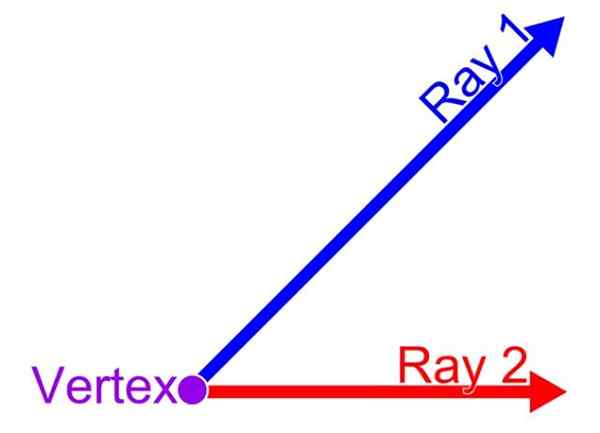 Elementen van een hoek. Bron: Wikimedia Commons.