Convergentie radiodefinitie, voorbeelden en oefeningen opgelost

Hij Convergentie straal van een reeks krachten is de straal van de cirkel van convergentie waarnaar de serie convergeert. Deze cirkel strekt zich uit van de waarde die de basis van de krachten annuleert tot de dichtstbijzijnde singulariteit van de functie die bij de serie is gekoppeld.

Alle analytische functie F (z) Het heeft een reeks bevoegdheden geassocieerd rond een niet -singulair punt, genaamd Taylor -serie:

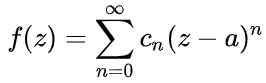
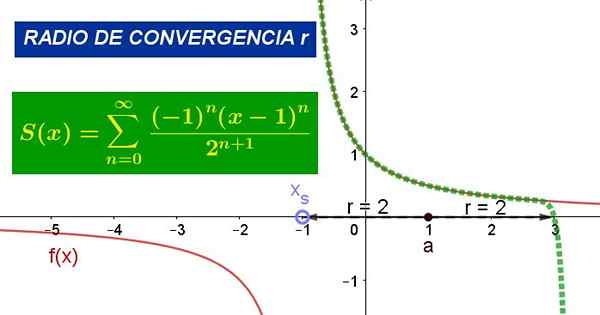
Figuur 1. De grafiek toont de power -serie rond waarde a = 1 voor functie f (x). De convergentiestraal is r = 2. Bron: Fanny Zapata.

Waar naar Het is het midden van de cirkel van convergentie, Z de onafhankelijke variabele van de functie en de C_N Het zijn coëfficiënten die verband houden met die van de functie F op het punt z = a.

De convergentiestraal R Het is een positief reëel getal dat de regio definieert:

| Z - A | < r

Waar de serie convergeert. Uit die regio de Diverge -serie, dat wil zeggen, er zijn oneindige waarden nodig. Wanneer de convergentiestraal oneindig is, convergeert de serie in het hele complexe vlak.

[TOC]

Hoe wordt de convergentiestraal bepaald?

Om een ​​serie te convergent zijn, is het noodzakelijk dat de absolute waarde van de opeenvolgende termen zal afnemen wanneer het aantal termen erg groot is. Op wiskundige manier zou het als volgt worden uitgedrukt:

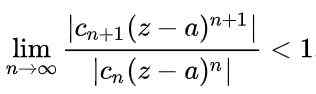
Met behulp van de eigenschappen van de limieten in de vorige uitdrukking wordt deze verkregen:

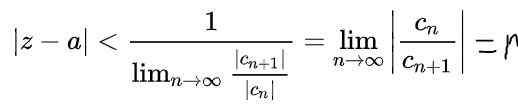
Hier R Het is de straal van convergentie en | Z - A | < r Het is de open randcirkel in het complexe vlak waar de serie convergeert. In het geval de waarde naar En de variabele z zijn reële getallen, dan zal het open interval van convergentie op de echte as zijn: (A - r, a+r).

Taylor -serie

De Taylor -serie van een functie F (x) Rond een waarde naar Waarin de functie oneindige derivaten heeft, is het een reeks bevoegdheden die wordt gedefinieerd als:

Het kan u van dienst zijn: Axioma van waarschijnlijkheid: typen, uitleg, voorbeelden, oefeningen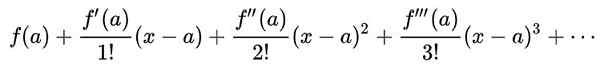

In de leefomgeving | X - A | < r, met R alsDe convergentiestraal van de serie, de Taylor -serie en de functie moeten zijn F (x) Ze vallen samen.

Aan de andere kant, de convergentiestraal R Het is de afstand van het punt naar en de singulariteit X_S Dichter bij het punt naar, De enkelvoudige punten zijn die waarden waar de limiet van de functie de neiging heeft om oneindig te zijn.

Dat is wanneer x → x_S Dus F → ± ∞.

Voorbeelden

voorbeeld 1

Zijn S (x) De krachten gegeven door de volgende uitdrukking:

S (x) = 1 - x + x²- X³+ X⁴-.. .+(-1)^N ⋅ x^N +.. .

Om de regio te bepalen waar de serie convergeert, berekenen we het quotiënt tussen de term (n-beeimo + 1) en de term (n-EME):

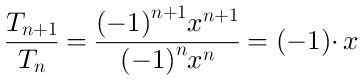
De absolute waarde van het voorste quotiënt is | x | en de limiet wanneer N → ∞ het is ook  | x |.

Om de serie te convergent zijn, is het noodzakelijk dat:

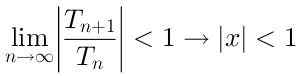
Dus de convergentiestraal van deze serie is R = 1, Omdat het convergeert voor de waarden van X die zich op een afstand van minder dan 1 ten opzichte van het centrum bevinden x = 0.

Voorbeeld 2

U wilt de Taylor -serie van de functie vinden f (x) = 1 / (1 + x) rond het punt x = 0 en bepaal de straal van de convergentie.

Om de serie te vinden, nemen we de opeenvolgende derivaten van de functie F (X), waarvan we de eerste drie zullen laten zien:

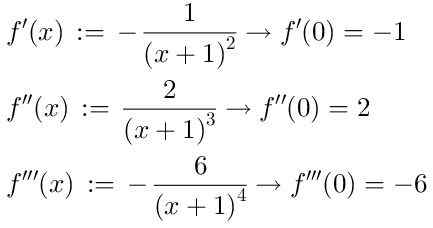
Rekening houdend met dat de nulorderterm van de Taylor -serie is:

 f (0) = 1,

De eerste bestelling: F '(0)/1!

Tweede bestelling:

 F "(0)/2!

Derde bestelling:

 f "(0)/3!

Enzovoort, de Taylor -serie van de gegeven functie is:

f (x) = 1 - x + x² - X³ + X⁴ -.. .+(-1)^N ⋅ x^N +.. .

Kan u van dienst zijn: Equilateral Triangle: kenmerken, eigenschappen, formules, gebied

Dat valt samen met de power -serie bestudeerd in Voorbeeld 1.

We hebben al gezegd dat de convergentiestraal van een Taylor -serie de afstand is van het midden van de uitbreiding in serie, die in ons geval de waarde is x = 0 tot de eerste singulariteit van de functie F (x). 

Omdat onze functie een singulariteit heeft (dat wil zeggen een oneindigheid) in x = -1, De afstand tussen de waarde -1 en het uitbreidingscentrum 0 is | -1 - 0 | = 1, Er wordt geconcludeerd dat de straal van de Taylor -serie convergentie is 1.

Dit resultaat valt volledig samen met het geval dat in voorbeeld 1 is verkregen door een andere methode.

Het feit dat de convergentiezone van de Taylor-serie het open interval is (-1, 1) impliceert dat de functie en serie samenvallen in dit interval, maar niet buiten hetzelfde.

Dat wordt weergegeven in figuur 2, waar 41 termen van de Taylor -serie zijn genomen, getekend door de continue blauwe lijn, terwijl de oorspronkelijke functie wordt getoond op de rode lijn van segmenten.

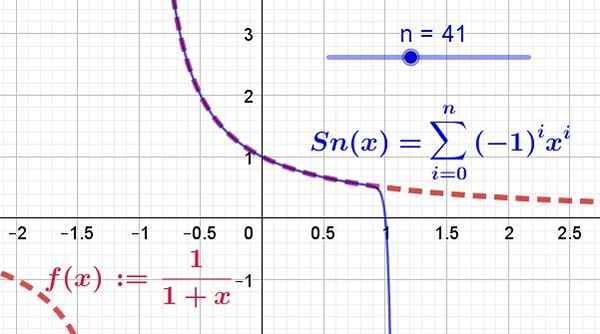Figuur 2. De functie f (x) (in rood) en de reeks krachten (of Taylor -serie in blauw) wordt getoond. Het kan worden gezien als de eerste 41 termen van de serie samenkomen tussen -1 en 1. Bovendien vallen de functie en de serie alleen samen in de convergentiegebied. (Bron: Fanny Zapata)

Opgeloste oefeningen

- Oefening 1

Overweeg dezelfde functie f (x) = 1 / (1 + x) van voorbeeld 2, maar deze keer wordt gevraagd om de Taylor -serie van genoemde functie rond het punt A = 1 te vinden.

Oplossing

We vinden de opeenvolgende voorwaarden van de serie, beginnend met de onafhankelijke term die F (1) = ½ is.

De volgende coëfficiënt die overeenkomt met de eerste bestellingstermijn is:

F '(1)/1! = -¼

De tweede bestelling is:

f "(1)/2! = 2/(2³ 2!))

Volg de derde bestellingscoëfficiënt:

Het kan u van dienst zijn: Tetradecágon

f "(1)/3! = -6 / (2⁴ 3!))

Enzovoort. De Taylor -serie zal zijn:

Sf (x) = ½ - 1/2² (X-1) + 1/2³(X-1)² - 1/2⁴ (X-1)³ + 1/2⁵ (X-1)⁴-..

- Oefening 2

Zoek de convergentiestraal van de vorige serie

Oplossing

We schrijven de term n -em en de term n-alkaus meer een:

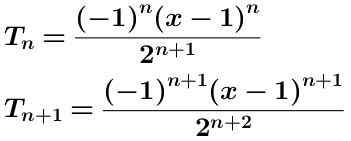We berekenen het quotiënt van deze twee termen die hieronder worden weergegeven, vereenvoudigd:

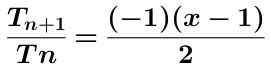
De absolute waarde van de vorige uitdrukking wordt genomen door te verkrijgen:

| X - 1 | / 2

Om de serie te convergent zijn, is het echter noodzakelijk dat het vorige bedrag strikt lager is dan de eenheid, dat wil zeggen:

| X - 1 | < 2

Die aangeeft dat de convergentiestraal rond de waarde x = 1 is:

R = 1

Aan de andere kant is de vorige uitdrukking gelijk aan dubbele ongelijkheid:

-2 < x - 1 < +2

Als we +1 toevoegen aan elk van de drie leden van de vorige uitdrukking, wordt dit verkregen:

-1 < x < 3

Dat is het serieconvergentie -interval.

Afbeelding 1 toont de oorspronkelijke functie en de Taylor -serie van genoemde functie rond punt X = 1. In de figuur kan worden geverifieerd dat de serie samenvalt met de functie in een omgeving van punt x = 1, maar binnen de convergentiestraal.

Referenties

1. CK-12 Foundation. Power Series: weergave van functies en bewerkingen. Hersteld van: CK12.borg.
2. Engler, a. 20199999999999999999999999999999999999999111 2019 2019 20199999 E moetene9999191999998311133113331322111152222222111231311111111111122111111111121111111111111111111111111111 -11111111111a's11111a's1a's1a's1a's1a's1a's D1a's Dam dat ’TO. Integrale calculus. Nationale Universiteit van de kust.
3. Larson, r. 2010. Berekening van een variabele. 9NA. Editie. McGraw Hill.
4. Gratis wiskundeteksten. Kracht series. Hersteld van: wiskunde.Liibretexts.borg.
5. Wikipedia. Kracht series. Hersteld van: is.Wikipedia.borg.
6. Wikipedia. Convergentiestraal. Opgehaald uit: in.Wikipedia.borg