Zeshoekige Prisma

We leggen uit wat een zeshoekig prisma is, de kenmerken, elementen, gebied, hoekpunten, randen en hoe ze te berekenen.

Wat is een zeshoekige prisma?

A Zeshoekige Prisma Het is een drie -dimensionaal lichaam dat bestaat uit twee zeshoekige vorm en zijkanten in de vorm van een rechthoek of parallellogram. Het kan in de natuur worden gevonden, in de kristallijne structuur van mineralen zoals beryllium, grafiet, zink en lithium, bijvoorbeeld.

De elementen van een zeshoekig prisma zijn de basis, het gezicht, de rand, de hoogte, de hoekpunt, de radio en de apothem. Van hen kunt u gebieden en volumes berekenen.

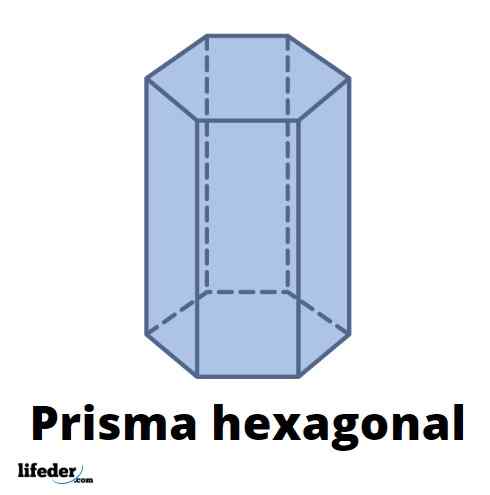
De bovenste figuur toont een zeshoekig prisma met rechthoekige zijgezichten; Het is te zeggen, Een rechte zeshoekige prisma. De zeshoeken van de bases zijn regelmatig, dat wil zeggen, hun interne kanten en hoeken zijn hetzelfde. Hexagonale prisma -gezichten kunnen echter onregelmatige zeshoeken zijn.

Kenmerken van zeshoekige prisma

1- Hexagonal Prism is een driedimensionale figuur met zeshoekige bases.

2- Er zijn een breed scala aan objecten die op deze definitie reageren en toch zijn ze heel anders.

In de volgende figuur zijn er verschillende zeshoekige prisma's: aan de linkerkant een recht zeshoekig prisma van reguliere gezichten, aan de rechterkant en naar beneden twee zeshoekige prisma's van onregelmatige gezichten. De zeshoek aan de basis van het onderstaande prisma heeft een bijzonderheid: het is concaaf, Wat betekent dat sommige van zijn interne hoeken groter zijn dan 180 °.

Variëteit aan zeshoekige prisma's. Bron: Wikimedia Commons.

Aan de andere kant zijn de zeshoekige bases van de bovenstaande prisma's polygonen convex: Alle interne hoeken meten minder dan 180 °.

Zeshoekige prisma -elementen

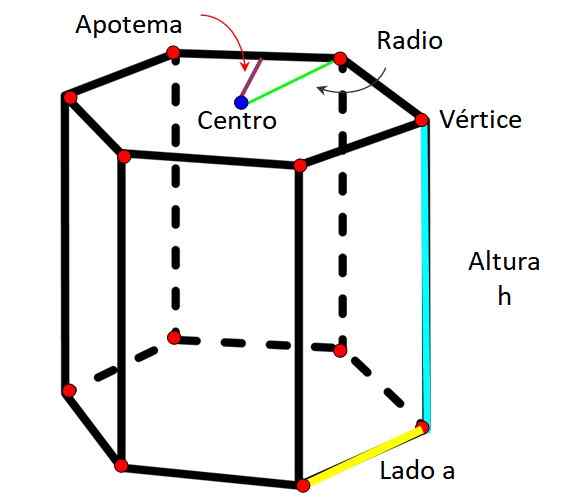Zeshoekige prisma -elementen. Bron: f. Zapata

Zoals elk prisma wordt zeshoekig prisma gekenmerkt door de volgende elementen te hebben:

Kan u van dienst zijn: multiplicatief inverse: uitleg, voorbeelden, opgeloste oefeningen

-Honken: In aantal van twee (2), in de vorm van zeshoek en congruent, dat wil zeggen van gelijke mate. Zeshoekige gezichten kunnen regelmatig of onregelmatig zijn.

-Gezichten: Een zeshoekig prisma heeft in totaal acht (8) gezichten, die kunnen worden geteld met figuur 1. Van de 8 gezichten zijn er twee (2) basen en zes (6) zijn lateraal.

-Rand: Het is het segment dat twee honken of twee kanten van het prisma verbindt.

-Hoogte: Het is de afstand tussen de twee gezichten van de prisma. Valt samen met de lengte van de rand in het geval van rechte prisma.

-Hoekpunt: gemeenschappelijk punt tussen een basis en twee zijzijden.

Als de basen van het prisma regelmatig zijn, maakt de symmetrie van de figuur mogelijk om extra elementen van de reguliere zeshoekige zijde te definiëren naar.

-Radio: Het is de afstand gemeten vanaf het midden van de zeshoek en elk hoekpunt.

-Apothem: Het is het segment dat van het midden van het zeshoekige gezicht naar het midden van één kant gaat.

Met behulp van deze elementen worden gebieden en volumes berekend, zoals we later zullen zien.

Formules

Er zijn talloze formules gerelateerd aan zeshoekige prisma. Ze dienen om het gebied van hun zijbases en gezichten te berekenen, het volume en andere belangrijke kenmerken. De gebieden van de reguliere zeshoek, onregelmatige zeshoek en parallellogram, evenals de perimeters, zijn nuttig.

Perimeter van een platte figuur

Het is de maat van zijn contour, die in het geval van een polygoon zoals zeshoek de som van zijn zijden is. Als de zeshoek regelmatig zijwaarts is naar, Er is een formule voor de omtrek P:

P = 6.naar

Regelmatig zeshoekig gebied

Laten we ALS en L bellen_NAAR Op het punt van apotheme. Het gebied wordt gegeven door:

Kan u van dienst zijn: niet -groepen gegevens: voorbeelden en oefening opgelost

A = P. L_NAAR/2 = 6a. L_NAAR/2

Waar P is de omtrek van de figuur.

Afhankelijk van de grootte van de zijkant naar, Het gebied kan ook worden berekend door:

A = 2.5981.naar²

Onregelmatig zeshoekig gebied

Er is geen specifieke formule, omdat het afhangt van de opstelling van de zijkanten, maar de zeshoek kan worden onderverdeeld in driehoeken, het gebied van elk berekenen en toevoegen.

Een andere methode om het gebied te vinden is die van Gauss -determinanten, waarvoor het nodig is om de coördinaten van zeshoekige hoekpunten te kennen.

Parallellogramgebied

A = basis x hoogte

Ja naar is de basis en H Het is de hoogte, het gebied is:

A = A.H

Zeshoekige prismagebied

Het is de som van de gebieden van de bases -twee zeshoeken -en die van de gezichten -6 rechthoeken of parallellogrammen-.

Regelmatig zeshoekig prismagebied

Als het zeshoekige prisma de basis heeft in de vorm van gewone zeshoeken en de laterale randen loodrecht op deze basen staan, wordt het gebied gegeven door de som:

A = 2 x 2.5981.naar² + 6e.H

Waar naar Het is de kant van de zeshoek en H Het is de hoogte van het prisma.

Onregelmatig en rechte zeshoekige prismagebied

Als de basen onregelmatige zeshoeken zijn, wordt het gebied berekend door:

A = 2A_baseren  + P.H

Waar:

-NAAR_baseren Het is het onregelmatige zeshoekige basisgebied.

-P is de omtrek van de basis.

-H is de hoogte van de prisma

Hoekpunten

Elk zeshoekig gezicht heeft 6 hoeken of hoekpunten, wat in totaal 12 hoekpunten geeft voor het zeshoekige prisma.

Randen

Er is een formule om het aantal randen van een prisma te vinden. Het werd ontdekt door de grote wiskundige Leonhard Euler (1707-1783) en wordt gebeld Euler -stelling voor polyhedros. Zegt dit:

Kan u van dienst zijn: algebraïsch redeneren

Als C het aantal gezichten is, en de hoeveelheid Vértices V en de totale randen. Is het waar dat:

C+v = a+2

De bedragen voor het zeshoekige prisma zijn: C = 8 en V = 12. Daarom is a:

A = C + V - 2 = 8 + 12-2 = 18

Volume

Het volume V van enig prisma, recht of schuin, van gewone of onregelmatige gezichten, wordt gegeven door:

V = basisgebied x hoogte

Daarom hebben we de formules nodig voor het gebied dat we eerder hebben gezien.

Bijvoorbeeld, voor een recht zeshoekig prisma, wiens bases gewone zeshoeken zijn, wordt het volume gegeven door:

V = 2.5981.naar².H

Referenties

1. Math Open Referentie. Polygoongebied. Hersteld van: Mathpenref.com.
2. Wikipedia. Prisma. Hersteld van: is.Wikipedia.com.