Gewicht (fysieke) berekening, eenheden, voorbeelden, oefeningen

Hij gewicht Het is de kracht waarmee de aarde objecten naar het oppervlak trekt. Elke keer dat een object wordt gevallen, gaat dit naar de grond, het is niet in staat om zijn eigen middelen te beklimmen, noch wordt het niet halverwege, noch omdat de aarde het aantrekt.

Alle objecten trekken steevast met elkaar aan, zelfs de kleintjes, alleen dat de omvang van de kracht waarmee ze doen evenredig is met de massa. Dit betekent dat objecten met kleine massa weinig sterkte uitoefenen over anderen, maar hemelse lichamen zoals de aarde kunnen een zeer grote kracht uitoefenen.

De aarde houdt de maan ronddraaiend dankzij deze kracht van aantrekkingskracht, die wordt genoemd, die wordt genoemd Gravitationele aantrekkingskracht Als het gaat om objecten die ver van het aardoppervlak zijn, en gewicht Wanneer objecten dichtbij zijn.

Hieruit volgt dat de zwaartekracht niet vereist dat objecten noodzakelijkerwijs in contact zijn met elkaar om te handelen: daarom wordt gezegd dat het een afstandskracht is.

De objecten hebben nog steeds gewicht, zelfs als ze zich op een bepaalde hoogte op de grond bevinden en hoe massiever, hoe groter dit gewicht zal zijn.

De grote Engelse wetenschapper Isaac Newton was de eerste die een verklaring gaf over deze kwestie, door de universele zwaartekrachtwet die zijn naam draagt ​​en die sindsdien heeft gediend om te begrijpen hoe objecten omgaan met massa met massa met massa. Dit is erg belangrijk, omdat elk object op de planeet gewicht heeft.

[TOC]

Gewichtseenheden

Het internationale eenhedensysteem als het gewicht voor gewicht is Newton, genoemd ter ere van Isaac Newton. Dit is de eenheid om alle soorten krachten te meten.

De Newton, afgekort N, wordt gedefinieerd als de noodzakelijke kracht voor een massaobject van 1 kg om een ​​versnelling van 1 m/s te verwerven². Afgezien van de Newton zijn er andere eenheden van kracht van gemeenschappelijk gebruik, bijvoorbeeld het volgende:

De kilogram-kracht

Hij kilogram-force O Kilopondio, afgekort KG-F of KP, hoewel gewoonlijk KG zonder verder genoemd. Het is noodzakelijk om de locatie te specificeren, omdat zoals vermeld, het zwaartekrachtveld variaties ervaart met hoogte en breedtegraad.

Als iemand zegt dat dit 45 kg weegt, is het in werkelijkheid wat het betekent dat hun gewicht 45 kg-F is, omdat het kilogram de eenheid is die is gereserveerd voor de massa.

Kan u van dienst zijn: open circuit

De gelijkwaardigheid tussen kg-f en n is: 1 kg-f = 9.8 n

Het pond-force

De Libra-fuerza, Afgekort LB-F is ook een krachteenheid die analoog is aan de KG-F, omdat het de kracht is die de aarde uitoefent op een object van 1 pond massa. En net als bij de KG-F is er geen probleem met de waarden wanneer u op aarde bent, dat wil zeggen een object van de massa massa, weegt 1 lb-f-f-f-f.

De gelijkwaardigheid in LB-F en N is: 1 lb-f ≡ 4.44822 n.

Gewichtsberekening en formule

Het gewicht van een object is evenredig met zijn massa. Een grotere massa, groter gewicht.

De formule om de grootte van gewicht P te vinden (of ook w, zoals soms aangeeft, door "Gewicht" In het Engels) het is heel eenvoudig:

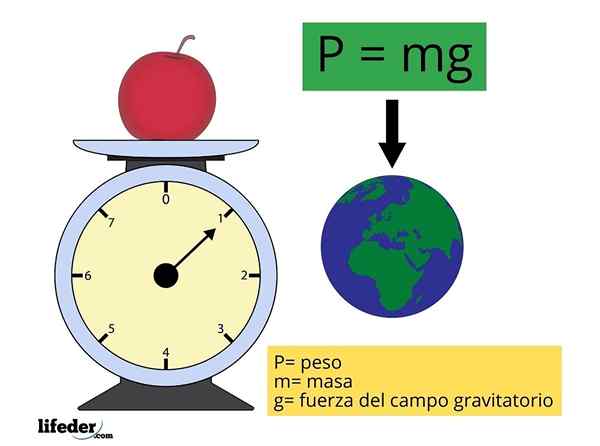
P = mg

Waar M vertegenwoordigt de massa van het object en G Het is de omvang van de versnelling van de zwaartekracht (intensiteit van het zwaartekrachtveld of ernst), ongeveer constant en waarvan de waarde wordt genomen als 9.81 m/s² Voor de meest voorkomende berekeningen.

Het gewicht is een vector en om onderscheid te maken tussen een vector en zijn grootte worden de gewaagde letters gebruikt. Op deze manier wordt bij PREN P Er wordt verwezen naar de vector:

P = M ∙G

De G Met gedurfde teksten is het het land van het land van zwaartekracht, dat wil zeggen de invloed die de aarde uitoefent op de ruimte die eromheen omringt, ongeacht of er een ander lichaam is dat het is of niet waarneemt. Elk object met massa heeft zijn eigen zwaartekrachtveld, klein of groot.

De intensiteit van het land van het land van het land G Het is niet helemaal constant. Het heeft kleine variaties die voornamelijk ontstaan ​​omdat de aarde geen perfecte sfeer is en ook voor lokale lengte- en dichtheidsverschillen. Maar voor de meeste toepassingen, waarde 9.81 m/s² Het werkt heel goed.

Andere hemellichamen hebben hun eigen karakteristieke zwaartekrachtveld, daarom verschilt de versnelling van de zwaartekracht volgens de planeet of satelliet. Hetzelfde object zou in elk een ander gewicht hebben, vandaar dat het gewicht geen karakteristieke eigenschap van dingen is, maar van het onderwerp in het algemeen.

Het gewicht als een vector

Het gewicht is een vector en heeft daarom een ​​grootte, richting en betekenis. In de buurt van het aardoppervlak is het gewicht een verticale vector en de richting is altijd naar beneden.

Over het algemeen wordt het verticale adres aangesteld als Axis En of Z, En de betekenis is toegewezen teken + of teken - om het te onderscheiden van de richting omhoog. De keuze hangt af van de locatie van de oorsprong. In het lagere beeld werd de oorsprong gekozen op het punt van waaruit de appel valt:

Kan u van dienst zijn: ideaal gas: model, gedrag, voorbeelden Het gewicht is een vector die verticaal naar beneden is gericht. Bron: f. Zapata.

De eenheidsvector J, Een vector van grootte gelijk 1, wordt gebruikt om verticale richting te wijzen en te onderscheiden. In termen van deze vector is het gewicht als volgt geschreven:

P = mg ( - J))

Waar een negatief teken wordt toegewezen aan de richting.

Verschillen tussen gewicht, massa en volume

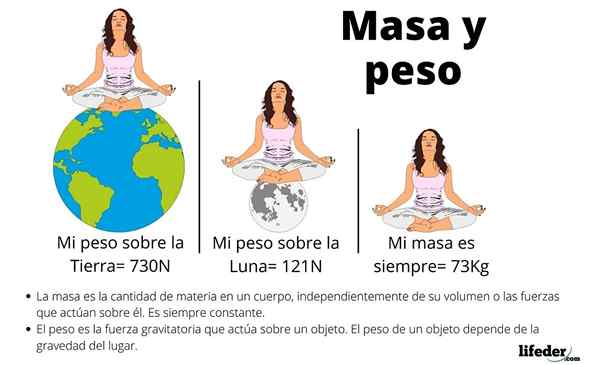
Vaak zijn deze drie concepten verward, maar het beoordelen van de kenmerken van het gewicht, is het gemakkelijk om het te onderscheiden van massa en volume.

Om te beginnen hangt het gewicht af van het zwaartekrachtveld van de plaats waar het object is. Bijvoorbeeld, op aarde en op de maan heeft hetzelfde een ander gewicht, hoewel de hoeveelheid atomen die het vormen constant is.

De massa is een scalaire grootte, gerelateerd aan de hoeveelheid atomen die het object vormen en wordt bewezen met de weerstand dat het object zijn beweging moet veranderen, een eigenschap genoemd luiheid.

Van zijn kant is het volume de maat voor de ruimte die wordt ingenomen door een object, een andere scalaire hoeveelheid. Twee objecten met gelijk volume wegen niet hetzelfde, bijvoorbeeld een ijzeren kubus weegt veel meer dan een ander polystyreen van dezelfde afmetingen.

Samengevat:

• De massa is gerelateerd aan de hoeveelheid materie die een lichaam heeft.
• Het gewicht is de kracht die door de aarde wordt uitgeoefend op die massa, evenredig daarmee.
• Volume is de ruimte die door materie wordt ingenomen.

Opgemerkt moet worden dat scalaire hoeveelheden zijn, noch de massa noch het volume richting of betekenis hebben, maar alleen numerieke waarde en een adequate eenheid. Aan de andere kant moet het gewicht, als een vector, altijd worden uitgedrukt om de grootte, eenheid, richting en betekenis te wijzen, zoals in de vorige sectie.

Voorbeelden van gewicht

Alle objecten op aarde hebben gewicht, u kunt zelfs objecten "wegen" die niet op aarde zijn, zoals andere planeten of de zon, hoewel het op indirecte middelen natuurlijk is.

Omdat het gewichtsbereik erg groot is, wordt wetenschappelijke notatie gebruikt (in krachten van 10) om sommige uit te drukken die erg groot of erg klein zijn:

-De zon: 1.989 × 10³⁰ kg-f

-Jupiter: 1.898 × ​​10²⁷ kg-f

-Een mug: 2.0 × 10^-5 N

-Baby's: 34.3 n

-Een kind: 353 n

-Volwassen persoon: 65 kg-f

-Een volwassen olifant: 5.5 × 10³ kg-f

-Blauwe walvis: 1.0 × 10⁶ N

Oefening opgelost

Een deegdoos 20 kg rust op een tafel.

a) Vind het gewicht van de doos en de normale kracht die de tabel erop uitoefent.

Kan u van dienst zijn: behoud van het lineaire momentum: principe, voorbeelden, oefeningen.

b) Nog eens 10 kg doos wordt op de eerste geplaatst. Zoek de normale die de tabel uitoefent op de doos van 20 kg en de normale die deze op de kleinste doos uitoefent.

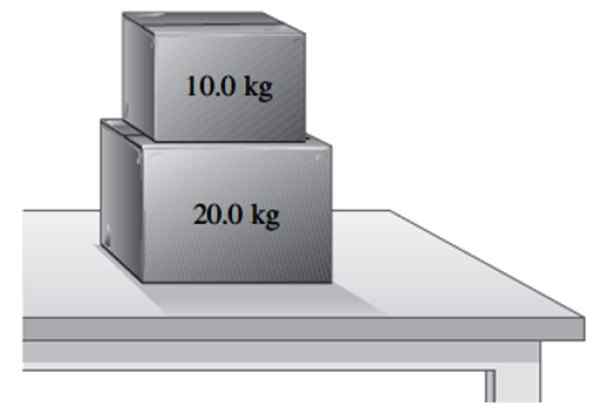Twee dozen die op een tafel rusten. Bron: f. Zapata.

Oplossing voor

Het is handig om een ​​vrij lichaamsdiagram op de doos te maken, dat bestaat uit het tekenen van de krachten die erop handelen.

In deze situatie is er nog steeds de kleinste doos bovenop, daarom zijn er slechts twee krachten: de eerste is het gewicht P die verticaal naar beneden wordt getrokken, zoals aangegeven in de voorgaande secties en dan is er de normale N, dat is de loodrechte kracht die de tabel uitoefent en voorkomt dat de doos valt.

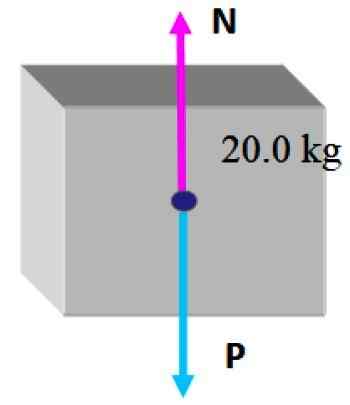
Aangezien de doos in deze omstandigheden in een statisch evenwicht is, is het redelijk om te concluderen dat de grootte van het normaal hetzelfde is als die van gewicht, zodat deze kan compenseren, daarom:

N = mg = 20.0 kg x 9.8 m/s² = 196 n; verticaal gericht.

Van zijn kant is het gewicht p = 196 n verticaal gericht.

Oplossing B

Nu worden nieuwe vrije lichaamsdiagrammen gemaakt over beide objecten. Voor de grote doos veranderen dingen een beetje, omdat de kleine doos er kracht op uitoefent.

De krachten zijn als volgt: N En P Ze zijn respectievelijk de normale die de tafel uitoefent en het gewicht op de doos van 20.0 kg, dat is niet veranderd. En de nieuwe kracht die door de kleine doos wordt uitgeoefend, is N₁, het normale vanwege contact met de bovenkant van de grote doos.

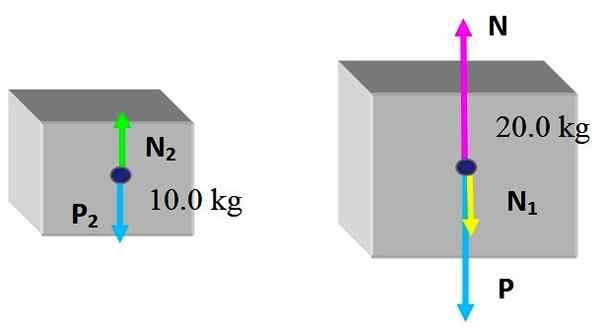
Wat betreft de kleine doos, het ontvangt het normaal N₂, Uitgeoefend door de bovenkant van de grote doos en natuurlijk het gewicht P₂. Omdat de dozen een statische balans zijn:

N₂ - P₂ = 0

N - n₁ - P = 0

Vanaf de eerste vergelijking moet je n₂ = P₂ = 10 kg x 9.8 m/s² = 98 n. Wet van actie en reactie, de grootte van de kracht die de kleine doos ontvangt, is hetzelfde dat deze op de grote doos uitoefent, dan:

N₂ = N₁ = 98 n

Van de tweede vergelijking wordt de normale n dat de tabel op de grote doos wordt gewist, die op zijn beurt de kleine doos bovenaan heeft:

N = n₁ + P = 98 n + 196 n = 294 n

Referenties

1. Figueroa, D. 2005. Serie: Physics for Science and Engineering. Deel 2. Dynamisch. Uitgegeven door Douglas Figueroa (USB).
2. Giambattista, een. 2010. Natuurkunde. 2e. ED. McGraw Hill.
3. Giancoli, D.  2006. Fysica: principes met toepassingen. 6e. Ed Prentice Hall.
4. Sears, Zemansky. 2016. Universitaire natuurkunde met moderne natuurkunde. 14e. ED. Deel 1. Pearson.
5. Serway, r., Jewett, J. 2008. Natuurkunde voor wetenschap en engineering. Deel 1. 7e. ED. Cengage leren.
6. Thomas Griffith, W. 2007. Conceptuele fysica. MC Graw Hill.