Drie -dimensionaal golven concept, typen en voorbeelden

Zijn Drie -dimensionale golven Degenen die zich in de ruimte verspreiden, bijvoorbeeld de geluidsgolf geproduceerd door een luidspreker. Deze golf verspreidt zich in alle richtingen, hoewel niet met dezelfde intensiteit in allemaal.

Als een verstoring op een bepaald punt in de ruimte optreedt, verspreidt deze zich in de drie ruimtelijke richtingen, waarbij de fronten voor de voorgolf worden gesloten, bolvormig, elliptisch of een ander type.

Drie -dimensionale golven geproduceerd door een spreker

Aan de andere kant, als de plaats waar de golven vandaan komen, dat wil zeggen dat de bron een vlakke verdeling heeft, dan zal de verstoring voornamelijk in de richting loodrecht op dat vlak reizen, waardoor platte golf fronten wordt gevormd.

[TOC]

Soorten drie -dimensionale golven

In drie -dimensionale golven zijn golffronten een reeks oppervlakken die zijn ondergedompeld in drie -dimensionale ruimte.

Nu is het golf front de geometrische plaats van de ruimtepunten die worden bereikt door de eerste verstoring, tegelijkertijd.

Drie soorten golven die reizen in de drie -dimensionale ruimte worden meestal beschouwd, volgens de symmetrie van de golffront: platte golven, cilindrische golven en bolvormige golven. Echte golven behoren echter niet altijd tot deze typen, omdat ze niet zo'n hoge mate van symmetrie hebben.

Platte golven

Een vlakke golf die snel in de positieve richting van de X reist, wordt functioneel weergegeven als:

G (x, t) = f (x - v⋅t)

Deze golf is niet beperkt tot de as X, maar strekt zich ook uit in de adressen En En Z. Maar de functionele vorm geeft aan dat alle punten met dezelfde X -coördinaat, ongeacht coördinaten (z, y), dezelfde G -waarde hebben.

In dit geval zijn de golf fronten vlakken parallel aan het z-en vlak dat snel vooruitgaat v, wat betekent dat de vlakke golf alle drie -dimensionale ruimte bezet.

De uitdrukking die een vlakke golf vertegenwoordigt die zich in elke richting verspreidt of snel v, waar of Vertegenwoordigt een eenheid Senior Vector Directeuren cos (α), cos (β) En cos (γ), is:

Kan u dienen: Reactie Enthalpy: Definitie, Thermochemie, Oefeningen

g = f (û • r - v⋅t) = f (x cos (α) + en cos (β) + z cos (γ) - v⋅t)

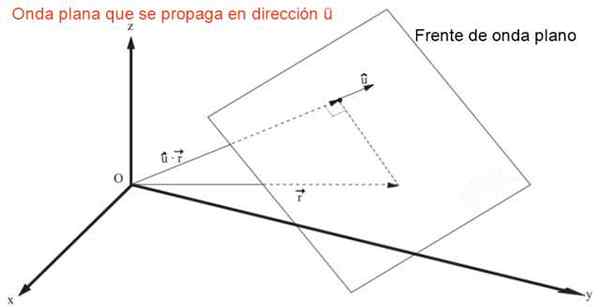Plat golffront dat zich in de drie -dimensionale ruimte snel verspreidt V. Bron: f. Zapata.

Het is gemakkelijk om, door directe vervanging, aan te tonen dat de vorige uitdrukking een oplossing is van de drie -dimensionale golfvergelijking, een vergelijking in gedeeltelijke derivaten van de tweede lineaire volgorde:

∂_XxG + ∂_YyG + ∂_ZZG = (1/V²) ∂_TTG

De vorige vergelijking kan compacter worden geschreven met behulp van de Laplacian -operator ∇²:

∇²G = (1/V²) ∂_TTG

Cilindrische golven

Wanneer de initiële verstoring over een rechte lijn wordt verdeeld, verspreidt de golf zich in de radiale richting loodrecht op die lijn die de drie -dimensionale ruimte die eromheen omringt, met cilindrische golf fronten vult.

Bolvormige golven

Wanneer de bron punctueel is en het medium waarin de drie -dimensionale golf wordt gepropageerd, is homogeen en isotrope (de eigenschappen veranderen niet volgens de richting), dan zijn de golf fronten concentrische sferen naar het punt waar de aanvankelijke verstoring optrad.

In het geval van een sferische golf waarin de intensiteit van de golf in alle richtingen identiek is, hangt de functie die de verstoring beschrijft alleen maar af van de afstand R naar de tijdige en tijdbron T.

In dit geval is de bijbehorende Laplacian:

∇²G = (1/r²) ∂_R(R² ∂_RG)

De golfvergelijking zijn:

∇²G = (1/V²) ∂_TTG

De algemene oplossing zou zijn:

g (r, t) = (1/r) f (r - v⋅t) + (1/r) g (r + v⋅t)

In dit geval wordt gezegd dat het een bolvormige golf. Maar er kunnen varianten zijn, zoals hieronder te zien is

Niet -isotrope bolvormige golven

Het kan ook gebeuren dat een sferische golf, dat is, met de golf fronten gevormd door concentrische bollen naar een centraal punt, de amplitude of intensiteit van de golf is anders in de verschillende richtingen.

Dit is wat er gebeurt wanneer de centrale bron van de golf in een richtingen efficiënter is dan andere. 

Het kan je van dienst zijn: natuurkunde voor de Grieken (Antigua Griekenland)

Het geluid dat door een hoorn wordt geproduceerd, heeft bijvoorbeeld niet overal dezelfde intensiteit, zelfs niet in het geval van hoorn -equidate punten.

De intensiteit is niet hetzelfde, hoewel het signaal dezelfde tijd nodig heeft om deze punten te bereiken. Het is een sferische golf met een niet -speldig directioneel patroon. 

Er zijn ook bolvormige golven in het geval van elektromagnetische golven gecreëerd door een antenne, maar ze zijn misschien niet even intens in alle richtingen.

Zenderantenne

Niet -homogeen helft

Wanneer het medium niet homogeen is, is de snelheid van de voortplanting van de golf in verschillende richtingen anders.

Een voorbeeld van een niet -homogeen medium is de atmosfeer waarin er drukverschillen zijn met hoogte en er zijn temperatuurgradiënten. Een ander voorbeeld is de lagen van de korst van de aarde, die verschillen in dichtheid en elastische module. 

Niet-homogeniteit resulteert in de golf fronten die uit een centrale punctuele bron afkomstig zijn, zijn geen concentrische bollen, omdat de afstand die door de golf wordt afgelegd, in dezelfde periode, in elke richting anders is.

Dan is er een drie -dimensionale golf waarvan de golffront niet bolvormig is.

Intensiteit en energie van een bolvormige golf

We kunnen de uitdrukking van een sferische harmonische golf zoals deze schrijven:

g (r, t) = (g_of / r) cos (k⋅r - ω⋅t)

Waar golf fronten zich snel verspreiden aan:

V = ω/k

En de amplitude neemt af met het omgekeerde van de afstand R van de punctuele bron van bolvormige golven.

Harmonische golven hebben energiedichtheid (Energie per volume -eenheid) ε gegeven door:

ε = ½ ρ ω² (G_of / R)²

In deze vergelijking:

-ρ Het heeft massa -eenheden per volume -eenheid en vertegenwoordigt de dichtheid van het medium waar een geluidsgolf zich voortplant.

-G_of Het is de amplitude van de verplaatsing van een element van het medium, bijvoorbeeld een vloeistof, vanwege de propagatiegolf.

Kan u van dienst zijn: viskeuze wrijving (kracht): coëfficiënt en voorbeelden

Opgemerkt moet worden dat, omdat het een sferische golf is, de energiedichtheid afneemt met het omgekeerde van het vierkant van de afstand.

De intensiteit van de golf, dat wil zeggen, de energie die per tijdseenheid wordt verzonden, is:

I = V⋅ε

Zoals altijd is de belangrijkste omvang in de praktijk het vermogen per gebied van een eenheid tot radiale afstand R:

P = v⋅ε = i_of / R²

Wezen Je_of = ½ ρ V ω² G_of².

De totale energie die per tijdseenheid wordt verzonden door een straal R is:  P⋅4πr²= 4π⋅i_of, En zoals verwacht hangt het niet af van de radiale afstand. 

Voorbeelden van drie -dimensionale golven

Drie -dimensionale golven zijn zeer frequent, dus we hebben:

Elektromagnetische golfbemiltantennes

De golven geproduceerd door een antenne of het geluid geproduceerd door een toets zijn drie -dimensionale golven, hoewel van verschillende aard

Ze bestrijken een zeer breed spectrum, van de radiogolven tussen de honderden KHz en honderden MHz, tot de golven die worden uitgestoten door de antenne van de antenne Wifi van de orde van de GHz, die al in het bereik van magnetrons vallen. 

We weten dat magnetron, hoewel ze geen ioniserende straling zijn, ze in staat zijn om de temperatuur van het organisme te verhogen omdat het veel water bevat.

Daarom is het niet raadzaam om de wifi-antenne in de buurt van het hoofd of lichaam te hebben. Ga gewoon een beetje weg, want op dubbele afstand is de intensiteit een kwart.

Seismische golven

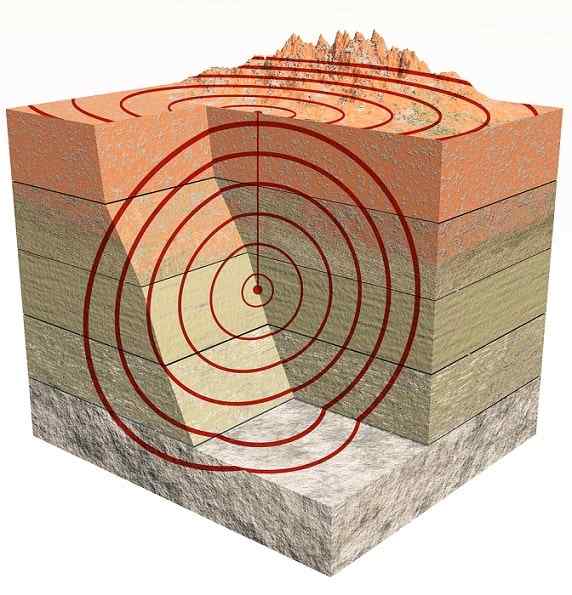Seismische golven

Het zijn ook drie -dimensionale golven. Voornamelijk zijn er die van het type P die compressiegolven en typen zijn S Wat zijn snijden of afscheuren (sHoren in Engels).

De golven P of primair zijn de eerste die aankomen omdat ze zich sneller verspreiden dan golven S of secundair.

Geluid

Geluid door te spreken

Geluid is een drie -dimensionaal golftype. Deze golven verspreiden zich in alle richtingen, hoewel, zoals we eerder hebben gezegd, niet met dezelfde intensiteit in alle richtingen.

Dit komt omdat de geluidsbron niet altijd uitstraalt met perfect bolvormige symmetrie.

Referenties

1. Baranek, l. 1969. Akoestiek. 2e. Editie. McGraw Hill.
2. Griffiths G. Lineaire en niet -lineaire golven. Hersteld van: Scholaredia.borg.
3. Nottoli, h. 2004. Fysica toegepast op architectuur. Nobuko.
4. Whitham G.B. 199999. Lineaire en niet -lineaire golven. Wiley. 
5. Wikiwaves. Niet -lineaire golven. Hersteld van: wikiwaves.borg