Stationaire golvenformules, kenmerken, typen, voorbeelden

De staande golven Het zijn golven die zich in een beperkte helft verspreiden, gaan en komen in een deel van de ruimte, in tegenstelling tot reizende golven, die wanneer zich propageren weggaan van de bron die hen oorsprong heeft en er niet naar terugkeert.

Ze vormen de basis van de geluiden die in de muziekinstrumenten worden geproduceerd, omdat ze gemakkelijk op de vaste snaren ontstaan, hetzij aan een van de uiteinden of beide. Ze zijn ook gemaakt in gespannen membranen zoals drums of binnenbuizen en structuren zoals bruggen en gebouwen.

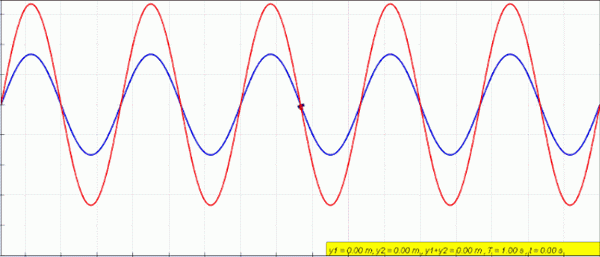Animatie van een stationaire (rode) golf gecreëerd door de superpositie van een linker (blauw) en rechter golf (groen). Bron: Lookangmany Dankzij de auteur van de originele simulatie = Wolfgang Christian en Francisco Schembre Auteur van Easy Java Simulation = Francisco Schembre/CC BY-SA (https: // creativeCommons.Org/licenties/by-sa/4.0)

Wanneer u aan beide uiteinden een vast touw heeft, zoals een gitaar, worden golven bijvoorbeeld gemaakt met identieke amplitude en frequentie, die in tegengestelde zintuigen reizen en een fenomeen worden geproduceerd dat wordt genoemd interferentie.

Als de golven in fase zijn, zijn de richels en valleien uitgelijnd en resulteren in een golf met dubbele amplitude. In dat geval is er sprake van constructieve interferentie.

Maar als de golven die interfereren uit fase zijn, ontmoeten de richels van de ene de valleien van anderen en de amplitude die resulteert is nul. Het is dan een destructieve interferentie.

[TOC]

Formules en vergelijkingen

De belangrijkste elementen van de golf om het in ruimte en tijd weer te geven, zijn de amplitude A, zijn golflengte λ en zijn hoekfrequentie ω.

Elementen van een golf. Bron: Wikimedia Commons.

In wiskundige weergave heeft het de voorkeur om k te gebruiken dan de Golfnummer o aantal keren dat de golf per eenheid plaatsvindt. Daarom wordt het gedefinieerd door de lengte van de λ -golf die de afstand is tussen twee valleien of twee richels:

K = 2π/ λ

Terwijl de hoekfrequentie Het is gerelateerd aan de periode of duur van een volledige oscillatie, zoals:

Ω = 2π/ t

En ook de frequentie F wordt gegeven door:

F = ω / 2π

Daarom:

F = 1/t

Bovendien bewegen de golven met snelheid v volgens:

v = λ.F

Wiskundige uitdrukking van de stationaire golf

Wiskundig kunnen we een golf uiten door de sinusfunctie of cosinusfunctie. Stel dat er golven van gelijke amplitude A zijn, golflengte λ en frequentie ω, zich verspreiden langs een touw en in tegengestelde zintuigen:

En₁ = Een sin (kx - ωt)

En₂ = Een sin (kx + ωt)

Bij het toevoegen van ze vinden we de resulterende golf en_R:

En_R = Y₁ + En₂ = Een sen (kx - ωt) + a sin (kx + ωt)

Er is een trigonometrische identiteit om de som te vinden:

Kan u van dienst zijn: wat is relatieve en absolute ruwheid?

sin α + sin β = 2 sin (α + β)/2 . cos (α - β)/2

Door deze identiteit, de resulterende golf en_R is overgebleven:

En_R = [2a sen kx] . cos ωt

Locatie van knooppunten en buik

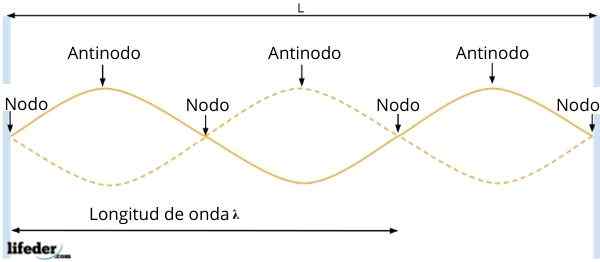Antinodos of buiken en knooppunten

De resulterende golf heeft een amplitude_R = 2ase kx, die afhangt van de positie van het deeltje. Dan, op de punten waarvoor sen kx = 0, wordt de amplitude van de golf geannuleerd, dat wil zeggen dat er geen trilling is.

Deze punten zijn:

Kx = π, 2π, 3π ..

Als k = 2 π/ λ:

(2 π/ λ) x = π, 2π, 3π ..

x = λ/2, λ, 3λ/2 ..

Op dergelijke punten treedt destructieve interferentie op en ze worden genoemd knooppunten. Ze worden gescheiden door een afstand gelijk aan λ/2, zoals afgeleid uit het vorige resultaat.

En tussen twee opeenvolgende knooppunten zijn de Antinodos of buik, waarin de amplitude van de golf maximaal is, omdat de constructieve interferentie optreedt. Ze komen voor wanneer:

sin kx = ± 1

Kx = ± π/2, 3π/2, 5π/2 ..

Opnieuw k = 2 π/ λ en vervolgens:

x = λ /4, 3λ /4, 5λ /4, ..

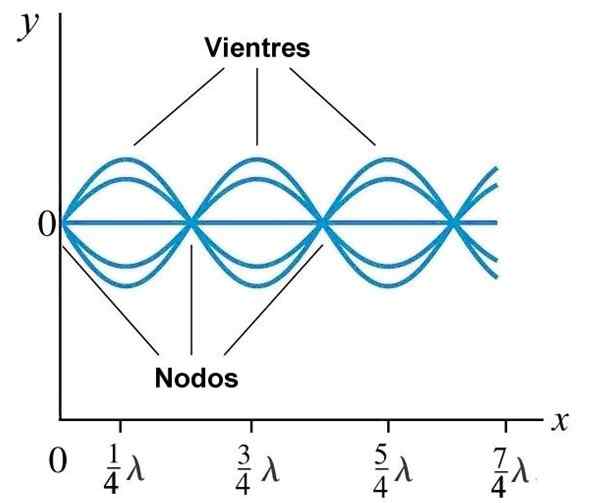Buik of antinodes en knooppunten in een stationaire golf gegenereerd op een touw met vast uiteinde bij x = 0. Bron: Wikimedia Commons.

Normale modi op een touw

De grensomstandigheden op het touw bepalen hoe golflengten en frequenties zijn. Als een touw in lengte L wordt bevestigd aan zijn twee uiteinden, kan het niet trillen met enige frequentie, omdat de punten waar het touw is vastgesteld al knooppunten zijn.

Bovendien is de scheiding tussen aangrenzende knooppunten λ/2, en tussen knooppunt en buik is het λ/4, alleen op deze manier worden bepaalde golflengten geproduceerd stationaire golven: die waarin een geheel getal n van λ/2 binnenin wordt aangepast de:

(λ/2) = l, met n = 1, 2, 3, 4 .. .

Daarom:

λ = 2l/n

De harmonischen

De verschillende waarden λ worden opgeroepen harmonischen. We hebben dus:

-Eerste harmonisch: λ = 2l

-Tweede harmonische: λ = l

-Derde harmonisch: λ = 2 l/3

-Harmonische kamer: λ = l/2

Enzovoort.

Snelheid en frequentie

Hoewel de stationaire golf niet lijkt te bewegen, is de vergelijking nog steeds geldig:

v = λ. F

Daarom:

v = (2l/n) . F

F = NV/2L

Nu kan worden aangetoond dat de snelheid waarmee een golf in een touw beweegt, afhangt van de T -spanning in dezelfde en de lineaire massa -dichtheid van massa μ (massa per lengte -eenheid) als:

Daarom:

Kan u van dienst zijn: dode belastingen: kenmerken, berekening, voorbeelden

Kenmerken van stationaire golven

-Wanneer de golven stationair zijn, verspreidt de resulterende golf zich niet als zijn componenten, die van de ene plaats naar de andere gaan. Er zijn punten waar y = 0 omdat er geen trilling is: de knooppunten, met andere woorden, de amplitude_R Het is nul.

-De wiskundige uitdrukking van een stationaire golf bestaat uit het product van een ruimtelijk deel (dat afhangt van de X -coördinaat of de ruimtecoördinaten) en een tijdelijk onderdeel.

-Onder de knooppunten oscilleert de resulterende zwarte golf op de ene plaats, terwijl de golven die van de ene plaats naar de andere gaan daar verouderd zijn.

-Alleen in de knooppunten wordt energie niet getransporteerd, omdat dit evenredig is met het kwadraat van de amplitude, maar zit vast tussen de knooppunten.

-De afstand tussen aangrenzende knooppunten is de helft van de golflengte.

-De punten waarop het touw is vastgesteld, worden ook beschouwd als knooppunten.

Jongens

Stationaire golven in een dimensie

De golven in een vast touw zijn voorbeelden van stationaire golven in een dimensie, wiens wiskundige beschrijving we in de vorige secties hebben aangeboden.

Stationaire golven in twee en drie dimensies

Stationaire golven kunnen ook worden gepresenteerd in twee en drie dimensies, die een iets complexere wiskundige beschrijving zijn.

Racing ondas voorbeelden

Vaste snaren

-Een string vastgelegd door extreme die met de hand of met de ene zuiger door de andere wordt gescilleerd.

Muziekinstrumenten

Stationaire golven worden gemaakt in muziekinstrumenten zoals Violoncello. Bron: Pixabay.

-Bij het spelen van stringinstrumenten zoals gitaar, harp, viool en piano.

Stlover -golven worden ook gemaakt in luchtbuizen, zoals orgelbuizen.

Gebouwen en bruggen

Stationaire golven ontstaan ​​in structuren zoals bruggen en gebouwen. Een opmerkelijk geval was dat van de Tacoma Narrows Suspension Bridge in de buurt van de stad Seattle, Verenigde Staten. Kort nadat hij in 1940 was ingehuldigd, stortte deze brug in vanwege de stationaire golven die in de wind werden gecreëerd.

De windfrequentie kwam overeen met de natuurlijke frequentie van de brug, waardoor hierin in stationaire golven werd gecreëerd, die hun amplitude toenamen totdat de brug instortte. Het fenomeen staat bekend als resonantie.

Het kan u van dienst zijn: lichte reflectie

Seiches

In de poorten is er een zeer nieuwsgierig fenomeen genoemd Seiche, waarin de golven van de zee grote oscillaties produceren. Dit komt omdat de wateren in de haven behoorlijk ingesloten zijn, hoewel de oceanische wateren om de zoveel tijd doordringen door de ingang van de haven.

Poortwateren bewegen met hun eigen frequentie, evenals die van de oceaan. Als beide wateren overeenkomen met hun frequenties, is er een grote stationaire golf vanwege resonantie, zoals gebeurde met de Tacoma -brug.

De Seiches Ze kunnen ook voorkomen in meren, reservoirs, zwembaden en andere waterlichamen beperkt door oppervlakken.

Vissentanks

Stationaire golven kunnen worden gecreëerd in een door een persoon getransporteerde viskomer, als de frequentie waarmee de persoon gelijk is aan de frequentie van de zwaai van het water.

Oefening opgelost

Het gitaartouw heeft L = 0.9 m en lineair deegdichtheid μ = 0.005 kg/m. Het wordt onderworpen aan 72 N spanning en de trillingsmodus is degene die de figuur toont, met amplitude 2a = 0.5 cm.

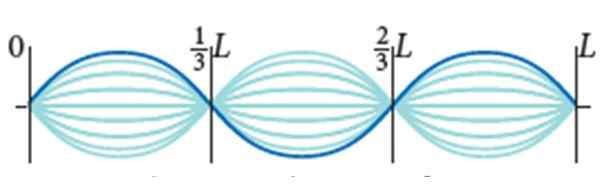Stationaire golven op een gitaartouw. Bron: Bauer, W. Fysiek.

Vinden:

a) Voortplantingssnelheid

b) golffrequentie

c) De overeenkomstige stationaire golfvergelijking.

Oplossing voor

Door:

Is verkregen;

V = [72 n/(0.005 kg/m)]^1/2  = 120 m/s.

Oplossing B

De afstand tussen twee aangrenzende knooppunten is daarom λ/2:

(2/3) l - (1/3) l = λ/2

(1/3) l = λ/2

λ = 2l/3 = 2 x 0.90 m / 3 = 0.60 m.

Zoals v = λ.F

F = (120 m/ s)/ 0.60 m = 200 s^-1= 200 Hz.

Oplossing C

De vergelijking is:

En_R = [2a sen kx] . cos ωt

We moeten waarden vervangen:

K = 2π/ λ = k = 2π/ 0.60 m = 10 π/3

F = ω / 2π

Ω = 2π x 200 Hz = 400 π Hz.

De 2A -amplitude wordt al gegeven door de verklaring:

2a = 0.5 cm = 5 x 10 ^-3 M.

Daarom:

En_R = 5 x 10 ^-3 M . sin [(10π/3) x] . cos (400πt) =

= 0.5 cm . sin [(10π/3) x] . cos (400πt)

Referenties

1. Bauer, W. 2011. Fysica voor engineering en wetenschappen. Deel 1. MC Graw Hill.
2. Figueroa, D. (2005). Serie: Physics for Science and Engineering. Deel 7. Golven en kwantumfysica. Uitgegeven door Douglas Figueroa (USB).
3. Giancoli, D.  2006. Fysica: principes met toepassingen. 6e. Ed Prentice Hall.
4. Serway, r., Jewett, J. (2008). Natuurkunde voor wetenschap en engineering. Deel 1. 7e. ED. Cengage leren.
5. Tipler, p. (2006) Natuurkunde voor wetenschap en technologie. 5e ed. Deel 1. Redactioneel teruggekeerd.
6. Wikipedia. Seiche. Hersteld van: is.Wikipedia.borg.