Geregistreerde hoek van een cirkeldefinitie, stellingen, voorbeelden

Hij geregistreerde hoek van een cirkel Het is degene die zijn hoekpunt heeft op de omtrek en zijn semi -strak is droog of raaklijnd naar hetzelfde. Als gevolg hiervan zal de geregistreerde hoek altijd convex of plat zijn.

In figuur 1 worden verschillende hoeken geregistreerd in hun respectieve omtrek weergegeven. De hoek ∠edf wordt geregistreerd door zijn hoekpunt D op de omtrek te hebben en zijn twee semi -recengers [van) en [df) de omtrek te drogen. 

Figuur 1. Verschillende ingeschreven hoeken over hun respectieve omtrek. Bron: f. Zapata met Geogebra.

Evenzo is de hoek ∠hgi geregistreerd, voor het hebben van zijn hoekpunt in de omtrek en zijn droge zijden naar hetzelfde.

De hoeken ∠kjr en ∠ust zijn ook geregistreerd bij de omtrek. De eerste heeft de ene Secant -kant en de andere raaklijn, terwijl de tweede zijn twee kanten heeft op de omtrek en een vlakke vlakhoek (180º) vormt.

Sommige auteurs noemen een semi-ingeschreven invalshoek voor degene die een van zijn zijden heeft die naar de omtrek raakt, maar in dit artikel wordt hij beschouwd als geregistreerd.

Elke geregistreerde hoek definieert of onderaf een boog geassocieerd met hetzelfde. Bijvoorbeeld in figuur 2 de geregistreerde hoek ∠ABC de boog a⌒c van lengte d onderdrukt.

Dezelfde figuur toont de hoek ∠doe, die niet in de omtrek is geregistreerd omdat hij zijn hoekpunt niet op zijn omtrek heeft, maar in het midden of.

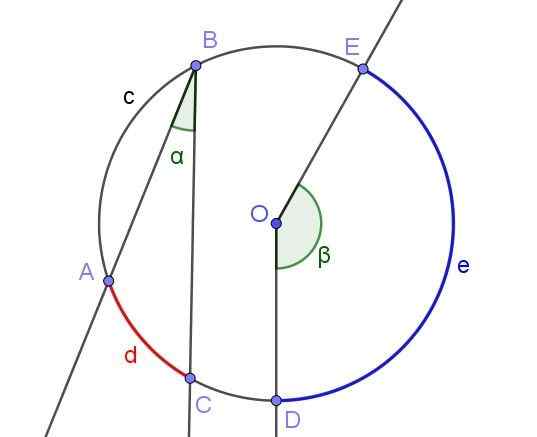Figuur 2. Geregistreerde hoek ∠abc en centrale hoek ∠doe. Bron: f. Zapata met Geogebra.

[TOC]

Centrale hoek

Naast de geregistreerde hoek, de centrale hoek, dat is degene wiens hoekpunt zich in het midden van de omtrek bevindt en waarvan de zijden naar de omtrek worden gesneden.

Kan u van dienst zijn: verschil tussen een gemeenschappelijke fractie en een decimaal aantal

De radianen meten van een centrale hoek is het quotiënt tussen de boog die onderaf, dat wil zeggen, de omtrekboog tussen de zijkanten van de hoek, en de straal van de omtrek.

Als de omtrek eenheid is (straal 1), dan is de lengte van de boog in dezelfde radio -eenheden de maat voor de hoek in radianen.

En wanneer de maat voor de hoek in graden vereist is, wordt de maatregel vermenigvuldigd in radialen met factor 180º/π.

De meetinstrumenten met hoeken gebruiken altijd een centrale hoek en de lengte van de boog die door dit direct in graden wordt gekalibreerd. Dit betekent dat wanneer een hoek wordt gemeten, op de achtergrond wat wordt gemeten de lengte van de boog is die door de centrale hoek wordt ingediend.

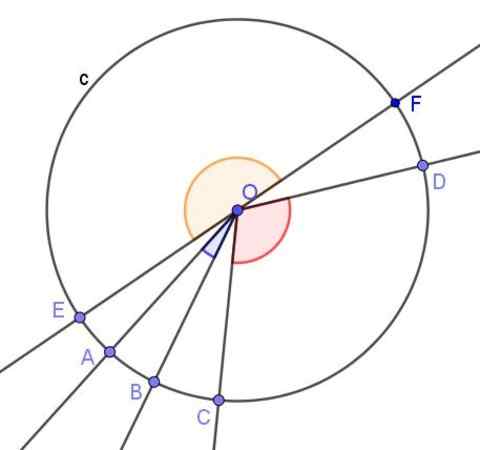figuur 3. Verschillende centrale hoeken van de omtrek. Bron: f. Zapata met Geogebra.

Stellingen

- Stelling 1 (geregistreerde hoek en centrale hoek)

De maat van een geregistreerde hoek is de helft van de maat van de centrale hoek, als beide hoeken onder dezelfde boog onder de onderkant zijn.

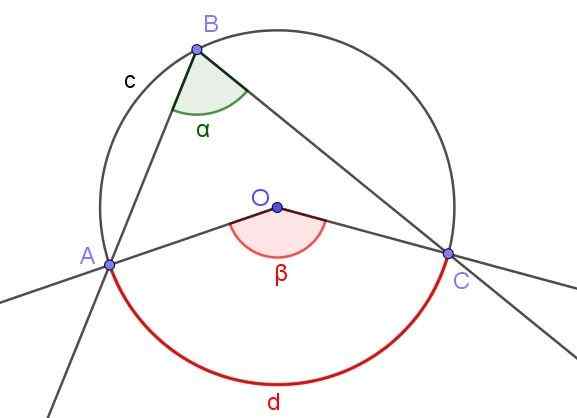Figuur 4. Geregistreerde hoek ∠ABC en centrale hoek ∠AOC die dezelfde boog A⌒c ondertitelen. Bron: f. Zapata met Geogebra.

Figuur 4 toont twee hoeken ∠ABC en ∠AOC, die dezelfde omtrekbogen kruisen A⌒c.

Als de maat van de geregistreerde hoek α is, dan is de β -maat van de centrale hoek twee keer de maat voor de geregistreerde hoek (β = 2 α) omdat beide dezelfde gemeten boog d aftrekken.

Demonstratie 1

Om Stelling 1 aan te tonen, zullen verschillende specifieke gevallen beginnen, tot het bereiken van de algemene zaak.

Kan u van dienst zijn: Sandwich Law: uitleg en oefeningen

Stel dat een geregistreerde hoek, waarin een van de zijkanten door het midden van de omtrek passeert, zoals getoond in figuur 5.

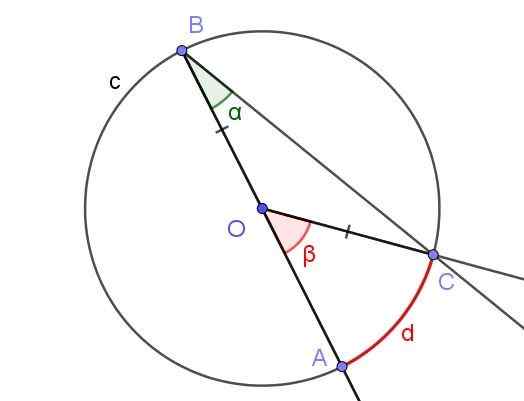Figuur 5. Geregistreerde hoek ∠abc met de zijde [BA) door O en centrale hoek ∠AOC. Bron: f. Zapata met Geogebra.

In dit geval wordt de Cob Heilelen Triange gevormd, omdat [oc] = [ob].

In een gelijkbenige driehoek zijn de hoeken naast de basis hetzelfde, daarom moeten ze ∠bco = ∠abc = α. Aan de andere kant ∠cob = 180º - β.

Gezien de som van de interne hoeken van de Cob Triangle die je hebt:

α + α + (180º - β) = 180º

Waar volgt dat 2 α = β, of wat equivalent is: α = β/2. Dit valt samen met welke stelling 1 stelt: de maat van de geregistreerde hoek is de helft van de centrale hoek, als beide hoeken hetzelfde touw indienen [AC].

Demonstratie 1B

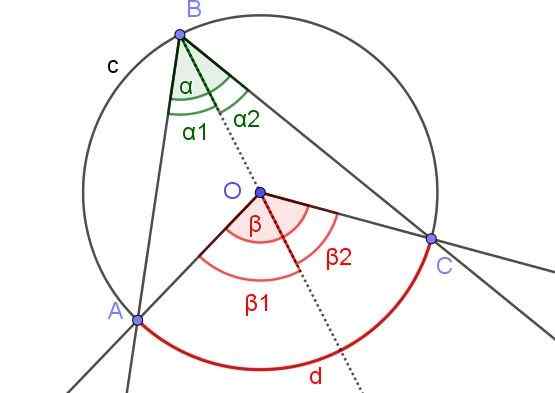Figuur 6. Hulpconstructie om aan te tonen dat α = β/2. Bron: f. Zapata met Geogebra.

In dit geval is er een ingeschreven hoek ∠abc, waarin het midden of de omtrek zich in de hoek bevindt.

Om Stelling 1 te demonstreren in dit geval wordt de semi -rechtse hulp [BO) getekend, zodat er twee geregistreerde hoeken ∠abo en ∠obc naast deze semi -recreational zijn.

Evenzo hebben ze de centrale hoeken β₁ en β₂ Grenzend aan genoemde semi -recreational. Op deze manier heb je dezelfde situatie als in demonstratie 1, dus er kan worden gezegd dat α₂ = β₂ /2 en α₁ = β₁ /2. Zoals α = α₁ + α₂ en β = β₁ + β₂ Er is daarom dat α = α₁ + α₂ = β₁ /2 + β₂ /2 = (β₁ + β₂) / 2 = β / 2.

Kan u van dienst zijn: soorten integralen

Concluderend α = β / 2, dat voldoet aan stelling 1.

- Stelling 2

Als twee of meer geregistreerde hoeken dezelfde boog subsen, dan hebben ze dezelfde maatregel.

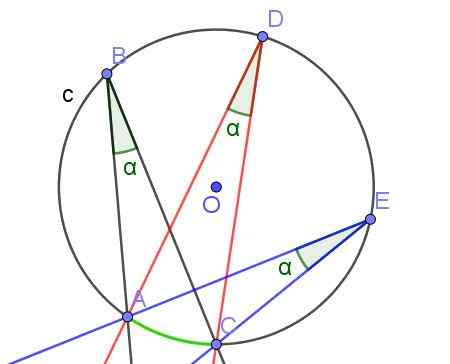Figuur 7. Geregistreerde hoeken van gelijke maatregel α, omdat ze dezelfde boog A⌒c subsen. Bron: f. Zapata met Geogebra.

- Stelling 3

De geregistreerde hoeken ondertit Er zijn snaren van dezelfde maatregel hetzelfde.

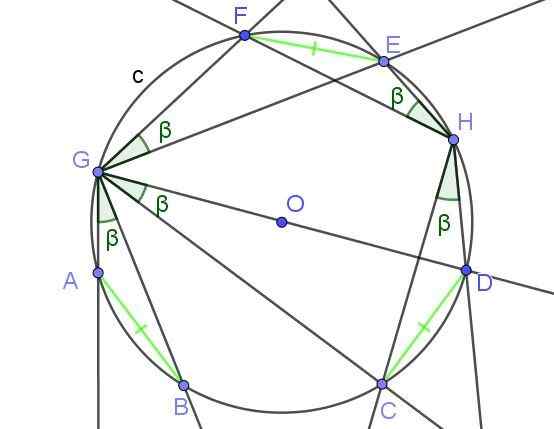Figuur 8. De ingeschreven hoeken die touwen van gelijke maatregel ondertekenen, hebben gelijke maat β. Bron: f. Zapata met Geogebra.

Voorbeelden

- voorbeeld 1

Toon aan dat de ingeschreven hoek subtites de diameter een rechte hoek is.

Oplossing

De centrale hoek ∠aob geassocieerd met diameter is een vlakke hoek, waarvan de maatregel 180º is.

Volgens Stelling 1 heeft elke hoek die in de omtrek is geregistreerd die hetzelfde touw onderdrukt (in dit geval de diameter), als maatregel de helft van de centrale hoek die hetzelfde touw ondertit, dat voor ons voorbeeld 180º/2 = 90º is.

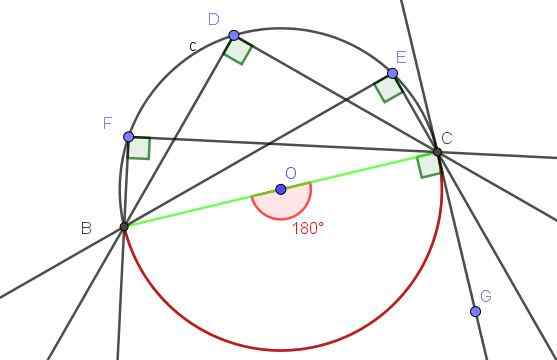Figuur 9. Elke geregistreerde hoek die onder de diameter van de diameter is, is een rechte hoek. Bron: f. Zapata met Geogebra.

- Voorbeeld 2

De lijn (BC) raaklijn in een A tot omtrek C, bepaalt de ingeschreven hoek ∠bac (zie figuur 10).

Controleer of stelling 1 van de geregistreerde hoeken is vervuld.

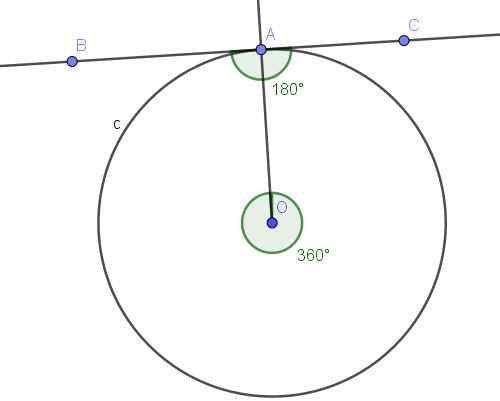Figuur 10. Geregistreerde hoek BAC en de convexe centrale hoek AOA. Bron: f. Zapata met Geogebra.

Oplossing

De hoek ∠bac is geregistreerd omdat het hoekpunt zich op de omtrek bevindt en de zijkanten [AB) en [AC) zijn geraakt aan de omtrek, dus wordt aan de definitie van ingeschreven hoek voldaan.

Aan de andere kant geeft de ingeschreven hoek ∠bac de A⌒a -boog, die de volledige omtrek is. De centrale hoek die de A⌒a -boog onderdrukt, is een convexe hoek waarvan de maatregel de volledige hoek is (360º).

De geregistreerde hoek subtites De volledige boog meet de helft van de bijbehorende centrale hoek, dat wil zeggen ∠bac = 360º/2 = 180º.

Met al het bovenstaande is bewezen dat dit specifieke geval voldoet aan stelling 1.

Referenties

1. Baldor. (1973). Geometrie en trigonometrie. Midden -Amerikaans cultureel redactioneel.
2. EN. NAAR. (2003). Geometrie -elementen: met oefeningen en kompasgeometrie. Universiteit van Medellin.
3. Geometrie 1e. Hoeken in de omtrek. Hersteld van: edu.Xunta.is/
4. Alle wetenschap. Voorgestelde oefeningen van hoeken in de omtrek. Hersteld van: Francesphysics.Blogspot.com
5. Wikipedia. Geregistreerde hoek. Hersteld van: is.Wikipedia.com