Hij Algebraïsche balansmethode Het wordt in de chemie gebruikt om het aantal atomen aan beide zijden van een chemische reactie te matchen. Een correct geschreven chemische reactie, moet de formules hebben van alle reagentia die aan de linkerkant deelnemen en de producten, ook met hun formules, aan de rechterkant.

Wanneer u echter een reactie hebt, is het aantal atomen in de formules van de reagentia gelijk aan dat van de respectieve atomen in de formules van de producten, niet altijd niet altijd.

Figuur 1. De algebraïsche balanceringsmethode is een eenvoudig hulpmiddel om chemische vergelijkingen in evenwicht te brengen. Bron: f. Zapata.

Het deeg wordt echter behouden. Laten we bijvoorbeeld de volgende reactie bekijken:

KCL₃ → KCl + O₂

Deze vergelijking heeft een verbinding genaamd kaliumchloraat, die wordt afgebroken door te verwarmen in kaliumchloride en gaszuurstof. Maar wanneer we zorgvuldig kijken, merken we dat er in het chloraatmolecuul 3 zuurstofatomen zijn, terwijl er rechts slechts één gaszuurstofmolecuul is met 2 atomen.

Wat dan wordt gedaan, is zich vermenigvuldigen met een numerieke coëfficiënt met het reagens van links, zodat het aantal atomen van alle deelnemende elementen voor en na de reactie hetzelfde is.

Maar ... wat is de waarde van deze coëfficiënt?

[TOC]

Manieren om vergelijkingen in evenwicht te brengen

In de vorige vergelijking is het eenvoudig om de juiste coëfficiënten te bepalen door inspectie. Als we met 2 aan de linkerkant vermenigvuldigen, hebben we 2 atomen van K, 2 van CL en 6 van O.

Daarom vermenigvuldigen we het kaliumchloride met 2 en de O₂ bij 3:

2 KCLO₃ → 2kcl + 3o₂

En nu kunnen we zien dat de boekhouding correct is aan beide zijden van de pijl en de reactie was in balans. Merk op dat andere numerieke waarden ook kunnen resulteren in een evenwichtige vergelijking, bijvoorbeeld:

Kan u van dienst zijn: boorzuur: chemische structuur, eigenschappen, voorbereiding, gebruik

4 KCLO₃ → 4KCL + 6o₂

De set van hele minimale getallen die gelijk zijn aan de hoeveelheid atomen aan beide kanten moet echter altijd worden gezocht.

De getallen die elke formule vermenigvuldigen, worden genoemd coëfficiënten. Het is heel belangrijk op te merken dat coëfficiënten kunnen worden toegewezen aan balans, maar subscripts moeten blijven zoals ze in elke formule verschijnen.

Noch kunnen coëfficiënten worden ingevoegd in het midden van de formule van elke verbinding, omdat het het zou veranderen.

Eenvoudige vergelijkingen zoals voorbeeld kunnen worden afgewogen door inspectie of score. Voor degenen die een beetje complexer zijn, is er een algebraïsche methode met een reeks eenvoudige stappen en elementaire rekenkundige bewerkingen hieronder gedetailleerd.

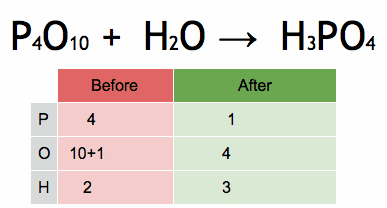Figuur 2. Animatie die het evenwicht van een chemische vergelijking toont om fosforzuur te verkrijgen. Bron: Wikimedia Commons. Efert/cc by-sa (https: // creativeCommons.Org/licenties/by-sa/4.0)

Stappen om een ​​chemische vergelijking algebraïstiek in evenwicht te brengen

Stap 1

-Wijs aan elk molecuul een willekeurige coëfficiënt toe, gesymboliseerd door een letter. Lyrics A, B, C, D .. ., indien nodig als nodig.

Belangrijk: Bedenk dat alleen een coëfficiënt wordt gebruikt door molecuul en nooit in het midden ervan wordt afgewisseld, deze wordt altijd aan de linkerkant geplaatst.

Stap 2

-Maak een lijst van elk deelnemende element.

Stap 3

-Plaats de coëfficiënt of coëfficiënten die aan elke verbinding naar links zijn toegewezen en matchen die rechts. Als er subscripts zijn, vermenigvuldigen ze zich met de coëfficiënt om het totale aantal atomen te vinden.

En als een element wordt gevonden in meer dan één molecuul, worden de hoeveelheden atomen die aan elke kant aanwezig zijn toegevoegd. Op deze manier de Gedeeltelijke vergelijkingen van elk element.

Stap 4

-Een numerieke waarde wordt toegewezen aan een van de coëfficiënten. Meestal is deze numerieke waarde 1 en wordt toegewezen aan de letter die meer keren verschijnt. Dit bereikt een eenvoudige vergelijking die dient als een startpunt om de andere coëfficiënten te vinden.

Kan u van dienst zijn: verdunningsfactor

Stap 5

-Bepaal de waarde van de volgende coëfficiënt door eenvoudige rekenkunde en vervang de waarde ervan in een andere vergelijking, om een ​​nieuw te verhogen.

Stap 6

-Herhaal de vorige stap om waarden te vervangen en een nieuwe vergelijking te maken, totdat u alle coëfficiënten vindt.

Stap 7

-Vervang de aldus vastberaden waarden. Als deze waarden geheel zijn, moet worden geverifieerd dat de vergelijking in evenwicht was. Als ze niet heel waren, wordt het vermenigvuldigd met het minimale gemeenschappelijke veelvoud van de noemers en het saldo is gecontroleerd.

Dan zullen we de toepassing van deze stappen in de resolutie van enkele voorbeelden visualiseren.

Opgeloste balansvoorbeelden

voorbeeld 1

Breng de volgende reactie indien nodig in evenwicht via de algebraïsche methode:

N₂OF₅ → n₂OF₄ + OF₂

Oplossing

We zien dat de reactie niet in balans is, want hoewel er 2 stikstofatomen aan beide zijden zijn, zijn de hoeveelheden aan de linkerkant en de rechterkant verschillend.

Dan moeten we de stappen volgen die in de vorige sectie worden beschreven:

-We schrijven de vergelijking opnieuw en vermenigvuldigen elk molecuul met een andere coëfficiënt. Kleine letters worden gekozen zodat ze niet verward zijn met de elementen:

A⋅n₂OF₅ → B⋅N₂OF₄ + C⋅O₂

-Nu noemen we elk element en passen we de hoeveelheden van dat element naar links en rechts overeen. Dit zijn de gedeeltelijke vergelijkingen voor elk element:

1. A⋅n₂ = B⋅N₂
2. A⋅o₅ = B⋅o₄ + C⋅O₂

-De coëfficiënt en het subscript vermenigvuldigen we verkrijgen het aantal stikstofatomen. Uit vergelijking 1 krijgen we:

2a = 2B

-Van vergelijking 2 hebben 5e zuurstofatomen links, terwijl rechts 4B En 2 c:

5a = 4b + 2c

-We wijzen waarde 1 toe aan coëfficiënt A, op deze manier:

A = 1

Deze keuze is willekeurig, hij kan ook worden gekozen als eerste B = 1.

-Deze waarden worden vervangen in vergelijking 2, om de waarde van C te bepalen:

Het kan u van dienst zijn: KUPRIC OXIDE (CUO)

5 = 4 + 2c

2c = 5-4 = 1

C = ½

-We vervangen de coëfficiënten in de oorspronkelijke vergelijking, de 1 is niet nodig om het expliciet te schrijven:

N₂OF₅ → n₂OF₄ + ½ O₂

-Omdat het de voorkeur verdient dat de coëfficiënten geheel zijn, wordt de gehele vergelijking vermenigvuldigd met het minimale gemeenschappelijke veelvoud van de noemers, die 2 en 1 zijn:

M.C.M. (1.2) = 2

Dan, door links en rechts te vermenigvuldigen met 2, wordt het verkregen:

2n₂OF₅ → 2n₂OF₄ + OF₂

En we tellen het aantal atomen aan beide kanten om de balans te controleren:

• N naar links: 4
• Of links: 10
• N aan de rechterkant: 4
• Of rechts: 8 + 2 = 10

Voorbeeld 2

Breng de volgende chemische reactie in evenwicht:

Nahco₃ → Na₂CO₃ + H₂Of + co₂

Oplossing

We vermenigvuldigen elk molecuul met een andere coëfficiënt:

A⋅ nahco₃ → b⋅na₂CO₃ + C⋅H₂O + D⋅co₂

Vervolgens stellen we de boekhouding van elk element naar rechts en links van de pijl voor. Er zijn in totaal 4 elementen in de reactie: natrium Na; Waterstof h; Auto -auto en zuurstof of, alles moet worden geteld:

• A⋅NA = B⋅NA₂
• a⋅h = C⋅H₂
• A⋅c = b⋅c + d⋅c
• A⋅o₃ = B⋅o₃+C⋅o+d⋅o₂

Volgens elke balans worden de volgende vergelijkingen verkregen:

1) A = 2B
2) a = 2c
3) A = B + D
4) A = 3B + C + 2d

De meest herhaalde coëfficiënt is naar, Daarom wijzen we de waarde 1 toe:

A = 1

Dus:

1) A = 2B ⇒ B = ½
2) a = 2c ⇒ c = ½
3) a = b + d ⇒ d = a - b = 1 - ½ = ½

We vervangen de coëfficiënten in de vergelijking:

Nahco₃ → ½. NA₂CO₃ + ½. H₂O + ½.CO₂

We vermenigvuldigen zich aan beide zijden van de pijl met 2, omdat dit de enige aanwezige noemer is, om de fractie te elimineren:

2nahco₃ → Na₂CO₃ +  H₂Of + co₂

We tellen het aantal aanwezige atomen aan de linkerkant: 2 atomen van Na, H en C en 6 van O. De lezer kan verifiëren dat elk van hen ook in dezelfde hoeveelheden rechts aanwezig is.

Referenties

1. Atkins, P. Principes van chemie: de paden van ontdekking. Pan -Amerikaans medisch redactioneel. 3e editie.
2. Briceño, J. USB Chemistry Guide. Hersteld van: GECOUSB.com.gaan.
3. Chang, R. 2013. Scheikunde. 11VA. Editie. Mc Graw Hill Education.
4. Opgeloste oefeningen. Algebraïsche balancering. Opgehaald uit: suelted oefeningen.co.
5. Simoza, l. Balancing van chemische vergelijkingen. Hersteld van: guao.borg.