Loodrechte lijnkenmerken, voorbeelden, oefeningen

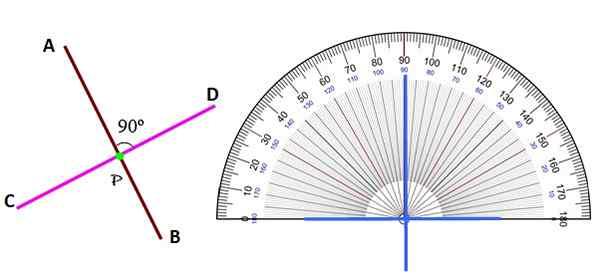
A loodlijn Het is er een die een hoek van 90º vormt ten opzichte van een andere lijn, curve of oppervlakte. Merk op dat wanneer twee lijnen loodrecht zijn en op hetzelfde vlak, wanneer ze worden gesneden, ze vier identieke hoeken vormen, elk van 90º.

Als een van de hoeken niet 90º is, wordt gezegd dat de lijnen schuin zijn. Legelijke lijnen komen vaak voor in ontwerp, architectuur en constructie, bijvoorbeeld het pijpnetwerk van de volgende afbeelding.

Figuur 1. Rechte -hoek buis en talloze loodrechte lijnen. Hoeveel hoeken van 90º kunnen in dit beeld worden geteld? Bron: PiqSels.

De oriëntatie van de loodrechte lijnen kan divers zijn, zoals die hieronder worden getoond:

Figuur 2. Loodrechte lijnen op het vlak. Bron: f. Zapata.

Ongeacht de positie, worden de loodrechte lijnen herkend door de hoek ertussen te identificeren als 90º, met behulp van de transportband.

Merk op dat in tegenstelling tot de parallelle lijnen in het vlak, die nooit kruisen, het loodrechte altijd op een punt P, genaamd, wordt genoemd voet van een van de lijnen aan de andere. Daarom zijn er ook twee loodrechte lijnen Secantes.

Elke lijn heeft er oneindig loodrecht op, omdat we door het AB -segment naar links of rechts op het CD -segment te verplaatsen, we een nieuwe loodrecht hebben met een andere voet.

Het loodrecht dat echter net door het middelpunt van een segment passeert, wordt echter genoemd bissectrice van genoemde segment.

[TOC]

Voorbeelden van loodrechte lijnen

Legelijke lijnen komen vaak voor in het stedelijke landschap. In de volgende afbeelding (figuur 3) slechts enkele van de vele loodrechte lijnen die worden gewaardeerd op de eenvoudige gevel van dit gebouw en zijn elementen zoals deuren, kanalen, stappen en meer: ​​meer:

Kan u van dienst zijn: Fourier Discreet getransformeerd: eigenschappen, toepassingen, voorbeelden figuur 3. Er zijn veel loodrechte lijnen op de gevel van een gemeenschappelijk gebouw zoals dit. Bron: Richard Kang door Flickr.

Het goede is dat drie lijnen loodrecht op elkaar helpen om de locatie van de punten en objecten in de ruimte vast te stellen. Zijn de coördinaatassen geïdentificeerd als X Axis, As y En Z -as, Duidelijk zichtbaar in de hoek van een rechthoekige kamer zoals de volgende:

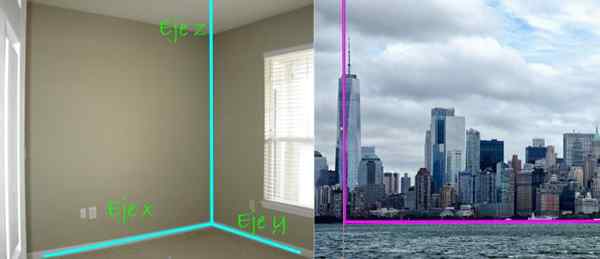Figuur 4. Het Cartesiaanse assysteem bestaat uit drie lijnen loodrecht op elkaar, elk heeft een voorkeursrichting in de ruimte. Links afbeeldingen credits: Treybunn 2 via Flickr. Rechte afbeelding; Needpix.

In het panoramische uitzicht op de stad, aan de rechterkant, wordt loodrechtheid tussen wolkenkrabbers en de grond ook gewaarschuwd. De eerste zou zeggen dat het in de Z -as, Terwijl de grond een vliegtuig is, dat in dit geval het vliegtuig is XY.

Als de grond het vliegtuig vormt XY, De wolkenkrabber staat ook loodrecht op elke weg of straat, die zijn stabiliteit garandeert, omdat een hellende structuur onstabiel is.

En op straat, waar rechthoekige hoeken ook loodrechte lijnen zijn. Veel wegen en straten hebben een loodrechte lay -out, op voorwaarde dat de land- en geografische ongevallen het toestaan.

Om de loodrechtheid tussen lijnen, segmenten of vectoren abrupt uit te drukken, wordt het symbool ⊥ gebruikt. Bijvoorbeeld als de lijn L₁ staat loodrecht op de lijn L₂, we schreven:

L₁ ⊥ l₂

Meer voorbeelden van loodrechte lijnen

- In het ontwerp zijn de loodrechte lijnen erg aanwezig, omdat veel gemeenschappelijke objecten gebaseerd zijn op vierkanten en rechthoeken. Deze vierhoekige vierzakken worden gekenmerkt door 90º interne hoeken te hebben, omdat hun zijkanten twee tot twee parallel zijn:

Het kan u van dienst zijn: algemene parabola -vergelijking (voorbeelden en oefeningen)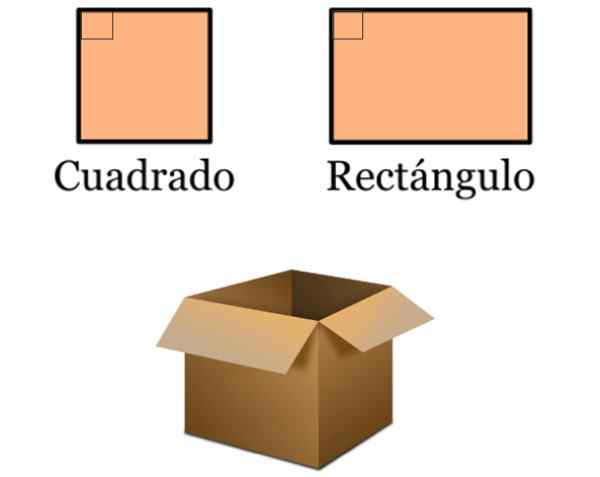 Figuur 5. Vierkanten en rechthoeken maken deel uit van talloze ontwerpen, zoals die van deze eenvoudige kartonnen doos om merchandise op te slaan. Bron: f. Zapata.

- De rechtbanken waarop verschillende sporten worden beoefend, worden afgebakend door talloze vierkanten en rechthoeken. Deze bevatten op hun beurt loodrechte lijnen.

- Twee van de segmenten waaruit een rechthoekige driehoek bestaat, staan ​​loodrecht op elkaar. Deze worden genoemd categorieën, Terwijl de resterende lijn wordt genoemd hypotenuse.

- De elektrische veldvectorlijnen staan ​​loodrecht op het oppervlak van een elektrostatisch evenwicht.

- Voor een geladen bestuurder staan ​​apparatuur en apparatuur altijd loodrecht op die van elektrisch veld.

- In pijpsystemen of kanalen die worden gebruikt om verschillende soorten vloeistoffen te transporteren, zoals gas dat in figuur 1 verschijnt, is het gebruikelijk voor ellebogen onder rechtse hoeken. Daarom vormen ze loodrechte lijnen, zoals een ketelruimte:

Figuur 6. Leidingen in een ketelruimte. Bron: Wikimedia Commons. Roger mclassus/cc by-s (http: // creativeCommons.Org/licenties/by-sa/3.0/)

Opdrachten

- Oefening 1

Teken twee loodrechte lijnen door regel en kompas.

Oplossing

Het is heel eenvoudig om deze stappen te volgen:

-De eerste regel wordt getrokken, AB (zwart) genoemd.

-Hierboven (of onder de voorkeur) van AB -markeringen Punt P, waar de loodrecht zal passeren. Als P net boven (of lager) de helft van AB staat, is deze loodrecht de bissector van het AB -segment.

-Met het kompas gecentreerd op P, wordt een cirkel getekend die AB in twee punten snijdt, geroepen tot 'en B' (rood).

Kan u van dienst zijn: vriendelijke of vriendelijke nummers: voorbeelden en hoe u ze kunt vinden

-Het kompas in A'P wordt geopend, het richt zich op een 'en er wordt een cirkel getrokken die door P (groen) gaat.

-Herhaal de vorige stap, maar open nu het kompas over de lengte van het B'P -segment (groen). Beide omtrekbogen worden gesneden op punt Q onder p en natuurlijk in het laatste.

-De punten P en Q zijn verbonden met de regel en de loodrechte lijn (blauw) is al klaar.

-Ten slotte moeten alle hulpconstructies zorgvuldig worden gewist, waardoor alleen loodrecht blijft.

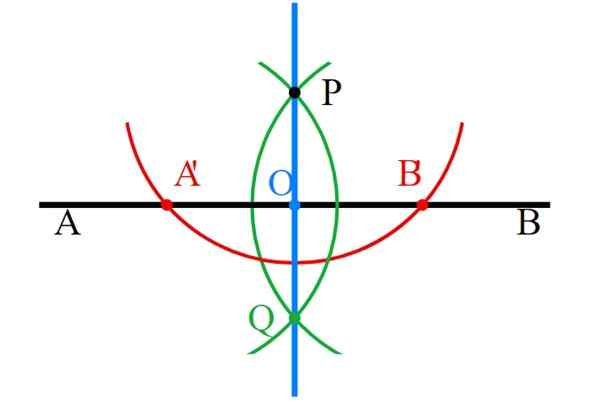Figuur 6. Percendulaire lijnen met regel en compas. Bron: Wikimedia Commons.

- Oefening 2

Twee lijnen l₁ en ik₂ Ze staan ​​loodrecht als hun respectieve hellingen m₁ en M₂ Ze vervullen deze relatie:

M₁ = -1/m₂

Gegeven de lijn y = 5x - 2, zoek een lijn er loodrecht op en passeer het punt (-1, 3).

Oplossing

-Allereerst is de helling van de loodrechte lijn m_⊥, Zoals aangegeven in de verklaring. De helling van de oorspronkelijke lijn is m = 5, de coëfficiënt die bij "x" hoort bij. Dus:

M_⊥= -1/5

-Dan wordt de vergelijking van de loodrechte lijn gebouwd en_⊥, De eerder gevonden waarde vervangen:

En_⊥= -1/5x + B

-Vervolgens wordt de waarde van B bepaald, met behulp van het punt gegeven door de verklaring, de (-1,3), omdat de loodrechte lijn er doorheen moet gaan:

y = 3

x = -1

Vervangen:

3 = -1/5 (-1) + B

De waarde van B wordt gewist:

B = 3- (1/5) = 14/5

-Eindelijk is de laatste vergelijking gebouwd:

En_⊥= -1/5x + 14/5

Referenties

1. Baldor, een. 2004. Flat and Space Geometry. Culturele publicaties.
2. Clemens, s. 2001. Geometrie met toepassingen en probleemoplossing. Addison Wesley.
3. Wiskunde is leuk. Evenwijdige lijnen. Hersteld van: Mathisfun.com.
4. Monterey Institute. Evenwijdige lijnen. Hersteld van: Montereyinstitute.borg.
5. Wikipedia. Evenwijdige lijnen. Hersteld van: is.Wikipedia.borg.