Kirchhoff -wet

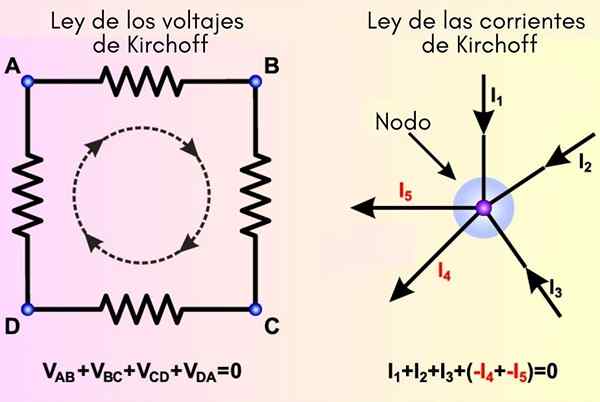
De wetten van Kirchoff komen respectievelijk voort uit de principes van energie en belastingbehoud. Links wordt de wet van de mazen vastgesteld en rechts de stromingen

Wat zijn de wetten van Kirchoff?

De Kirchoff -wet Ze bestaan ​​uit het toepassen van het principe van behoud van de elektrische lading en het principe van het behoud van energie op de elektrische circuits, om degenen die verschillende mazen hebben op te lossen.

Deze regels zijn, omdat ze geen wetten zijn in de strikte zin, te wijten aan de Duitse natuurkundige Gustav Kirchoff (1824-1887). Het gebruik ervan is essentieel wanneer de wet van Ohm niet voldoende is om spanningen en stromen in het circuit te bepalen.

Voorafgaand aan de verklaring en toepassing van de wetten van Kirchoff, is het handig om de betekenis te onthouden van enkele belangrijke concepten op elektrische circuits:

• Knooppunt: Union Point tussen twee of meer geleidende draden.
• Tak: Elementen van het circuit die tussen twee opeenvolgende knooppunten zijn, waardoor dezelfde stroom circuleert.
• Mazen: Traject of gesloten lus bestaande uit twee of meer takken en die in dezelfde richting wordt afgelegd, zonder hetzelfde punt te doorlopen.

Kirchoff's eerste wet

Het staat ook bekend als de wet van stromingen of regel van knooppunten, en stelt dat vast:

De som van de stromingen die een knooppunt binnenkomen, is gelijk aan de som van de stromen die eruit komen.

Dus op een wiskundige manier wordt de eerste wet uitgedrukt als:

∑ i = 0

Waar het symbool σ een som aangeeft.

De vorige vergelijking stelt vast dat, aangezien de elektrische lading niet wordt gecreëerd of vernietigd, de gehele stroom (belasting per tijdeenheid) die het knooppunt binnenkomt, gelijk moet zijn aan degene die eruit komt.

Kan u van dienst zijn: kunstmatige satellieten

Voorbeeld

Om de wet van de stromingen gemakkelijk toe te passen, wordt een bord toegewezen aan de binnenkomende stromingen en het tegenovergestelde teken van de uitgaande stromingen. De keuze is volledig willekeurig.

De volgende afbeelding toont twee stromen die een knooppunt invoeren, in rood getekend: i₁ en ik₂, en dat bij het vertrek ze in het groen worden getoond: de stromingen ik₃, Je₄ en ik₅.

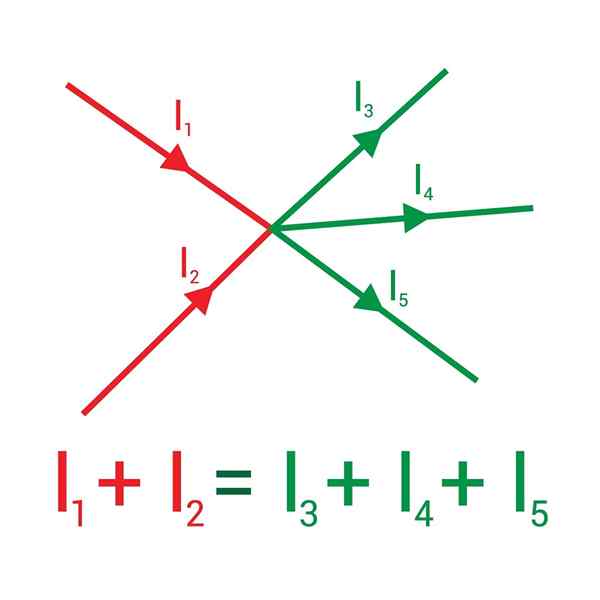De som van de stromen die een knooppunt invoeren, is gelijk aan de som van de stromen die eruit komen

Door het teken (+) toe te wijzen aan de inkomende stromingen, en de (-) aan het uitgaande, stelt de eerste regel van Kirchoff dat vast:

Je₁ + Je₂ - Je₃ - Je₄ - Je₅= 0 ⇒ i₁ + Je₂ = I₃ + Je₄ + Je₅

Kirchoff's tweede wet

Andere namen voor de tweede wet van Kirchoff zijn: Spanningswet, Spanningswetgeving of mesh wet. In elk geval stelt het vast dat:

De algebraïsche som van spanningsdruppels langs een gaas is gelijk aan 0.

Dit is een manier om het behoud van energie in het circuit toe te passen, omdat de spanning in elk element de verandering van energie per eenheid van belasting is.

Daarom is de algebraïsche som van de spanning bij het reizen van een gesloten gedeelte (een mesh) en kan de spanning toenemen en kunnen ze 0 worden geschreven:

∑ v = 0

Voorbeeld

In de volgende figuur heb je het gaas ABCDA, waardoor een stroom in de richting van de kloknaalden circuleert en de route kan beginnen op elk punt in het circuit.

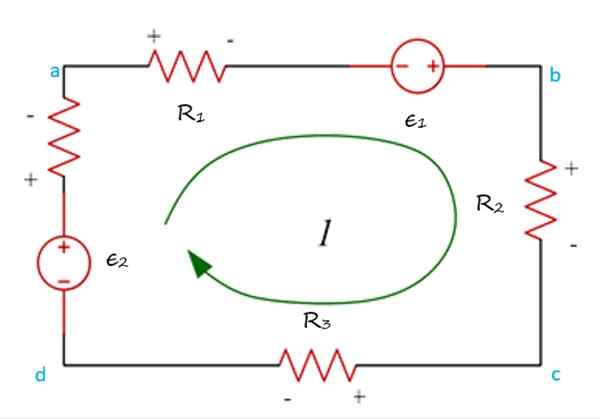Voorbeeld van een mesh tourde in een schema, waar wordt aangetoond dat de verhogingen en potentiële valpartijen de Kirchoff -spanningswet toepassen. Bron: f. Zapata.

Het is ook nodig. Het gebruikelijke is om de spanningsstijging als positief toe te wijzen, dat wil zeggen wanneer de stroom circuleert van ( -) naar (+). Vervolgens is de spanningsdaling, die optreedt wanneer de stroom van (+) naar ( -) gaat, negatief is.

Kan u van dienst zijn: siliciumoxide (SiO2): structuur, eigenschappen, gebruik, verkrijgen

Het starten van de mesh -route op punt "a", is de weerstand r₁. Daarin ervaren de belastingen een potentiële daling, gesymboliseerd door de borden (+) aan de linkerkant en ( -) boven de weerstand.

Daarom de spanning of spanning in r₁ Het heeft een negatief teken.

Dan bereikt u een directe spanningsbron, genaamd ε₁, wiens polariteit minder is (-) Meer (+). Daar gaan de elektrische ladingen door een potentiële stijging en deze bron wordt als positief beschouwd.

Volgens deze procedure voor de resterende weerstand en de andere bron wordt de volgende vergelijking verkregen als gevolg:

−v₁ + ε₁ - V₂ - V₃ + ε₂ = 0

Waar v₁, V₂ en v₃ zijn spanningen in weerstanden r₁, R₂ en r₃. Deze spanningen zijn te vinden uit de wet van Ohm: v = i · r.

Oefening opgelost

Zoek de waarde van stromingen i₁, Je₂ en ik₃ getoond in de figuur.

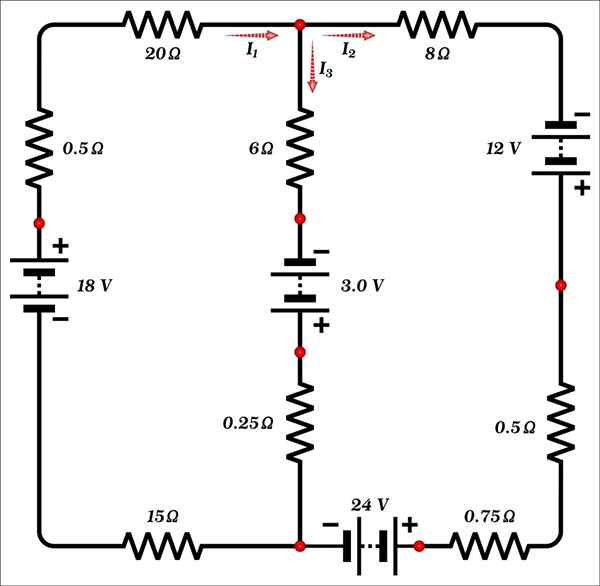
Oplossing

Dit circuit bestaat slechts uit twee mazen en heeft 3 onbekenden: de stromen en₁, Je₂ en ik₃, Er zijn dus ten minste 3 vergelijkingen nodig om de oplossing te vinden.

In het knooppunt (punt gemarkeerd in rood) dat bovenaan het circuit op de centrale tak staat, wordt waargenomen dat de stroom i₁ komt binnen, terwijl stromingen i₂ en ik₃ Ze zijn extravert.

Daarom leidt de Kirchoff Currents -wet tot de eerste vergelijking:

1) i₁ - i₂ - i₃ = 0

Het onderste knooppunt geeft dezelfde informatie, daarom is de volgende stap om de mazen te reizen.

Eerste gaas

Om de volgende vergelijking vast te stellen, wordt het gaas links in een schema gereisd, beginnend bij de linkerbovenhoek. Dit is de zin waarin stromingen en stromen circuleren₁ en ik₃.

Kan u van dienst zijn: Optische comparator: wat is het voor en onderdelen

Let daar op:

• Je₁ gaat door de weerstanden van 20 Ω, 15 Ω en 0.5 Ω en de 18 V -batterij, waar hij een potentiële stijging ervaart.
• Van zijn kant, ik₃ Het kruist de weerstanden van de centrale tak van 6 Ω en 0.15 Ω en op de 3 batterij.0 V is een potentiële stijging.

Evenzo wordt de ohm v = i ∙ r wet gebruikt om de spanning in elk verzet vast te stellen, volgens dit:

−20 ∙ i₁ - 6 ∙ i₃ + 3.0 - 0.25 ∙ i₃ −15 ∙ i₁ + 18.0 - 0.5 ∙ i₁ = 0

De voorwaarden bestellen:

(−20 −15 - 0.5) ∙ i₁ - (6 + 0.25) ∙ i₃  = - 3.0 - 18.0

−35.5 ∙ i₁ - 6.25 ∙ i₃ = - 21.0

2) 5 ∙ i₁ + 6.25 ∙ i₃ = 21.0

Tweede gaas

De derde vergelijking wordt verkregen door het gaas aan de rechterkant te touren, beginnend in het knooppunt van de bovenkant van het circuit. Er wordt opgemerkt dat:

• Je₂ Ga door de weerstanden van 8 Ω, 0.5 Ω en 0.75 Ω, plus 12 V en 24 V -batterijen. Volgens de polariteit van de batterijen is er in de route een toename van potentieel in de 12 V en afname van de 24 V.
• Belangrijk: De rondleiding door het tweede gaas (in een schema) is tegen I₃, Daarom zijn de spanningen in de weerstanden van 6 Ω en 0.25 Ω zijn potentiële stijgingen en dragen een positief teken. Volgens de polariteit van de batterijen is er een stijging van de 12 V en daalt in die van 24 V en 3 V.

Met dit alles bereik je:

−8 ∙ i₂ - 0.5 ∙ i₂ - 0.75 ∙ i₂ + 12.0 - 24.0 + 0.25 ∙ i₃ - 3.0 + 6 ∙ i₃ = 0

3) −25 ∙ i₂ + 6.25 ∙ i₃ = 15.0

Huidige berekening

Vergelijkingen 1), 2) en 3) vormen een systeem van 3 lineaire vergelijkingen met 3 onbekenden, waarvan de oplossing is:

Je₁ = 0.381 A; Je₂ = -0.814 a; Je₃ = 1.195 a

Het negatieve teken in stroom i₂ betekent dat het in de tegenovergestelde richting van het schema stroomt.