Coulomb Law -uitleg, formule en eenheden, oefeningen, experimenten

De Coulomb Law Het is de fysieke wet die de interactie tussen elektrisch geladen objecten regelt. Er werd gezegd door de Franse wetenschapper Charles Augustin de Coulomb (1736-1806), dankzij de resultaten van zijn experimenten door torsiebalans.

In 1785 ervoer Coulomb ontelbare tijden met kleine elektrisch geladen bollen, bijvoorbeeld om twee bollen te brengen of weg te nemen, variërend de grootte van zijn belasting en ook het teken. Altijd kijken en elk antwoord zorgvuldig registreren.

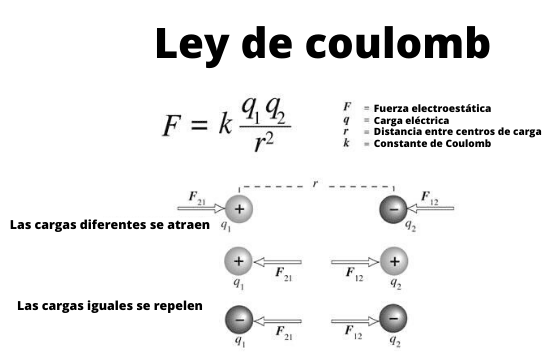
Figuur 1. Schema dat de interactie aantoont tussen specifieke elektrische ladingen door de wet van Coulomb.

Deze kleine bollen kunnen worden beschouwd als Specifieke belastingen, dat wil zeggen objecten waarvan de dimensies onbeduidend zijn. En ze vervullen, zoals bekend is sinds de tijd van de oude Grieken, dat de ladingen van hetzelfde teken worden afgestoten en die van een ander teken worden aangetrokken.

Figuur 2. Militaire ingenieur Charles Coulomb (1736-1806) wordt beschouwd als de belangrijkste natuurkundige in Frankrijk. Bron: Wikipedia Commons.

Met dit in gedachten vond Charles Coulomb het volgende:

-De kracht van aantrekkingskracht of afstoting tussen twee specifieke ladingen is recht evenredig met het product van de grootte van de belastingen.

-Deze kracht is altijd gericht langs de lijn die de ladingen aansluit.

-Ten slotte is de grootte van de kracht omgekeerd evenredig met het kwadraat van de afstand die de belastingen scheidt.

[TOC]

Formule en eenheden van de Coulomb -wet

Dankzij deze observaties concludeerde Coulomb dat de omvang van de kracht F Tussen twee specifieke kosten Q₁ En Q₂, gescheiden een afstand R, Het wordt wiskundig gegeven als:

Omdat kracht een vectorgrootte is, om het uit te drukken, is een eenheidsvector volledig gedefinieerd R In de richting van de lijn die de belastingen verbindt (een eenheidsvector heeft een grootte gelijk aan 1).

Bovendien wordt de noodzakelijke evenredigheidsconstante die de vorige uitdrukking transformeert in een gelijkheid die k wordt genoemd_En of gewoon k: de elektrostatische constante of Coulomb constant.

Ten slotte wordt de Coulomb -wet voor punctuele belastingen vastgesteld, gegeven door:

De kracht komt, zoals altijd in het internationale systeem van eenheden, in Newton (N). Wat betreft de aanklachten, de eenheid wordt Coulomb (C) genoemd ter ere van Charles Coulomb en uiteindelijk komt de afstand R in meters (M).

Het is aandachtig om de vorige vergelijking te observeren, het is duidelijk dat de elektrostatische constante eenheden van N moet hebben.M² / C², Om daardoor Newtons te verkrijgen. De waarde van de constante werd experimenteel bepaald als:

Kan u van dienst zijn: gratis vectoren: eigenschappen, voorbeelden, oefeningen

k_En = 8.89 x 10 ⁹ N.M² / C² ≈ 9 x 10 ⁹ N.M² / C²

Figuur 1 illustreert de interactie tussen twee elektrische ladingen: wanneer ze hetzelfde teken zijn, worden ze afgestoten, anders trekken ze aan.

Merk op dat de wet van Coulomb past bij de derde wet van Newton of de wet van actie en reactie, daarom de grootte van F₁ En F₂ Ze zijn hetzelfde, het adres is hetzelfde, maar de zintuigen zijn tegenover.

Hoe u de wet van Coulomb kunt toepassen

Om interacties tussen elektrische kosten op te lossen, moet rekening worden gehouden met het volgende:

- De vergelijking wordt uitsluitend toegepast in het geval van specifieke belastingen, dat wil zeggen elektrisch geladen objecten maar van zeer kleine afmetingen. Als geladen objecten meetbare dimensies hebben, is het noodzakelijk om ze in zeer kleine belastingen te verdelen en vervolgens de bijdragen van elk van deze belastingen toe te voegen, waarvoor uitgebreide berekening vereist is.

- Elektrische kracht is een vectorgrootte. Als er meer dan twee ladingen op elkaar inwerken, zijn de netto kracht op de belasting Q_Je Het wordt gegeven door het superpositieprincipe:

F_Netto = F_I1 + F_I2 + F_i3 + F_I4 +… = ∑ F_IJ

Waar het subscript J Vale 1, 2, 3, 4 ... en vertegenwoordigt elk van de resterende belastingen.

- Het moet altijd consistent zijn met de eenheden. De meest voorkomende is werken met de elektrostatische constante in eenheden als u ervoor moet zorgen dat de belastingen zich in Coulomb en de afstanden in meters bevinden.

- Ten slotte wordt de vergelijking toegepast wanneer de belastingen in een statisch evenwicht zijn.

Opgeloste oefeningen

- Oefening 1

In de volgende figuur zijn er twee specifieke belastingen +Q en +2q. Een derde punctuele belasting --q wordt op P geplaatst. Er wordt gevraagd om de elektrische kracht op deze belasting te vinden vanwege de aanwezigheid van de anderen.

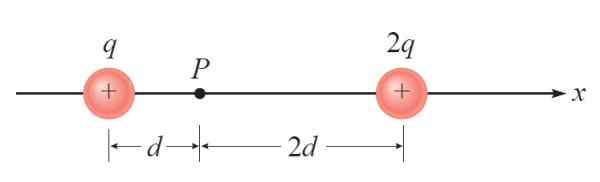figuur 3. Diagram voor het jaar opgelost 1. Bron: Giambattista, een. Natuurkunde.

Oplossing

Het eerste is om een ​​geschikt referentiesysteem op te zetten, dat in dit geval de horizontale as of x -as is. De oorsprong van dit systeem kan overal zijn, maar door comfort wordt het in P geplaatst, zoals weergegeven in figuur 4A:

Kan u van dienst zijn: Bethelgeuse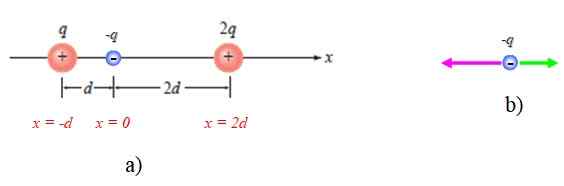Figuur 4. Schema voor het jaar opgelost 1. Bron: Giambattista, een. Natuurkunde.

Een schema van de krachten op -Q wordt ook getoond, rekening houdend met dat het wordt aangetrokken door de andere twee (figuur 4b).

Laten we bellen F₁ Naar de kracht die de belasting uitoefent die op de belasting -Q, ze worden gericht langs de X -as en wijst in negatieve zin, daarom:

De eenheidsvector in de richting van de x -as is X Met een circumflex -accent in de vergelijking. Dit is een veel voorkomende notatie voor een eenheidsvector. Het minder teken verschijnt omdat de kracht F₁ punten in de negatieve zin van de as.

Analoog wordt berekend F₂:

Merk op dat de omvang van F₂ Het is de helft van de F₁, Hoewel de belasting dubbel is. Om de netto kracht te vinden, worden ze eindelijk vectorly toegevoegd F₁ En F₂:

F_Netto = (-k + k/2).(Q² /D²) (X) N = - (k/2).(Q² /D²) (X) N

- Oefening 2

Twee polystyreen sferieten van gelijke massa m = 9.0 x 10^-8 kg heeft dezelfde positieve belasting q en worden opgehangen door een zijden draad in lengte l = 0,98 m. De bollen zijn gescheiden een afstand van d = 2 cm. Bereken de waarde van.

Oplossing

De situatie van de verklaring wordt beschreven in figuur 5A.

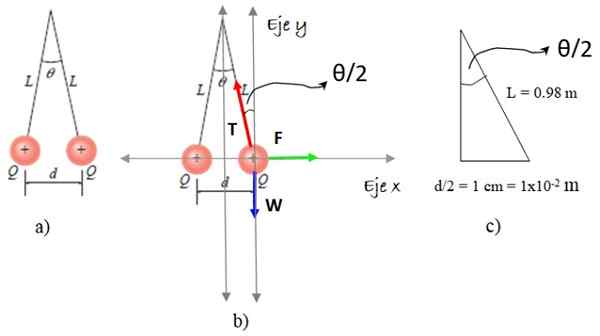Figuur 5. Schema's voor de oplossing van oefening 2. Bron: Giambattista, een. Fysica /f. Zapata.

We hebben een van de sferieten gekozen en daarop tekenen we het geïsoleerde lichaamsdiagram, dat drie krachten omvat: gewicht W, Touwspanning T en elektrostatische afstoting F, zoals verschijnt in figuur 5b. En nu de stappen:

Stap 1

De waarde van θ/2 wordt berekend met de driehoek van figuur 5c:

θ/2 = arcsen (1 x 10^-2/0.98) = 0.585º

Stap 2

Dan moet je de tweede wet van Newton toepassen en match 0, omdat de kosten in een statisch evenwicht zijn. Het is belangrijk om die spanning te benadrukken T Het is geneigd en heeft twee componenten:

∑f_X = -T.sin θ + f = 0

∑f_En = T.cos θ - w = 0

Stap 3

We wissen de omvang van de spanning van de laatste vergelijking:

Het kan u van dienst zijn: Dynamics: History, What Studies, Laws and Theories

T = w/ cos θ = mg/ cos θ

Stap 4

Deze waarde wordt in de eerste vergelijking vervangen om de grootte van F te vinden:

F = t sin θ = mg (sin θ / cos θ) = mg. TG θ

Stap 5

Zoals f = k q² /D², Het wist Q:

Door de numerieke waarden te vervangen die door de verklaring worden verstrekt, wordt deze verkregen:

Q = 2 × 10^-elf C.

Experimenten

Het controleren van de wet van Coulomb is eenvoudig door middel van een torsiebalans vergelijkbaar met die in zijn laboratorium.

Er zijn twee kleine bollen van Saúco, waarvan er één, die in het midden van de balans, wordt geschorst uit een draad. Het experiment bestaat uit het aanraken van de Saúco -bollen die zijn gedownload met een andere metalen bol geladen met belasting Q.

Figuur 6. Coulomb's torsiebalans.

Onmiddellijk wordt de lading gelijk verdeeld over de twee Saúco -bollen, maar dan, net als ladingen van hetzelfde teken, afstoten ze. Een kracht die de draadtorsie van de draad veroorzaakt en onmiddellijk weggaat van de vaste bol die op de gesuspendeerde bol werkt.

Dan zien we dat het een paar keer varieert totdat de balans bereikt. Dan wordt de torsie van de staaf of draad die deze vasthoudt in evenwicht gebracht door de elektrostatische afstotingskracht.

Als de bollen oorspronkelijk op 0 stonden, heeft de mobiele bol nu een hoek θ gekeerd. Omring van de balans is er een afgestudeerde tape in graden om deze hoek te meten. Bij eerder het bepalen van de torsieconstante, worden de afstotingskracht en de waarde van de lading verkregen door de Saúco -bollen gemakkelijk berekend.

Referenties

1. Figueroa, D. 2005. Serie: Physics for Science and Engineering. Deel 5. Elektrostatica. Uitgegeven door Douglas Figueroa (USB).
2. Giambattista, een. 2010. Natuurkunde. Tweede druk. McGraw Hill.
3. Giancoli, D.  2006. Fysica: principes met toepassingen. 6e. Ed Prentice Hall.
4. Resnick, r. 199999. Fysiek. Vol. 2. 3e ed. in het Spaans. Continental Editorial Company s.NAAR. van C.V.
5. Sears, Zemansky. 2016. Universitaire natuurkunde met moderne natuurkunde. 14e. ED. Deel 2.