Convergente lenskenmerken, typen en oefening opgelost

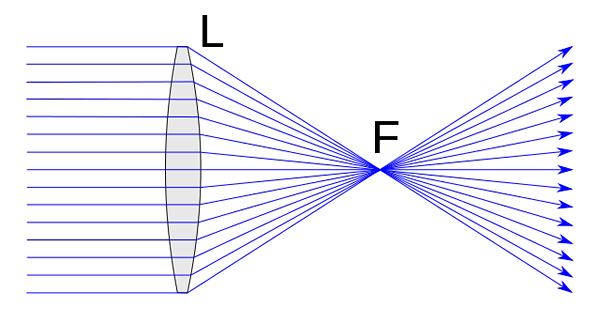
De Convergente lenzen Zij zijn degenen die dikker zijn in hun centrale en dunner deel aan de randen. Als gevolg hiervan concentreren ze zich (convergeren) op één punt de lichtstralen die hen parallel aan de hoofdas beïnvloeden. Dit punt wordt focus of beeldfocus genoemd en wordt weergegeven met letter F. Convergente of positieve lenzen vormen wat echte afbeeldingen van objecten worden genoemd.

Een typisch convergent lens voorbeeld is een vergrootglas. Het is echter gebruikelijk om dit type lenzen te vinden op veel complexere apparaten zoals microscopen of telescopen. In feite is een basisverbindingsmicroscoop die gevormd door twee convergente lenzen met een kleine focale afstand. Deze lenzen worden doelwit en oculair genoemd.

Vergrootglas, een convergente lens. 

Convergente lenzen worden gebruikt in optica voor verschillende toepassingen, hoewel misschien wel de bekendste is om defecten te corrigeren. Daarom zijn ze aangegeven om te handelen.

[TOC]

Kenmerken

Convergente lens. Chetvorno [CC0]

Convergente lenzen hebben een serie -functies die ze definiëren. In elk geval is het misschien wel de belangrijkste wat we al in de definitie hebben gevorderd. Aldus worden convergente lenzen gekenmerkt door de focus te verleggen elke straal die hen beïnvloedt in een richting parallel aan de hoofdas.

Bovendien is op een wederzijdse manier elke invallende straal die de focus passeert, parallel aan de optische as van de lens gebroken.

Convergente lenzen elementen

In het licht van uw studie is het belangrijk om te weten welke elementen de lenzen in het algemeen en convergente lenzen in het bijzonder vormen.

Over het algemeen wordt het het optische centrum van een lens genoemd tot het punt waarop elke straal die erdoorheen gaat, geen afwijking ervaart.

De hoofdas is de lijn die zich aansluit bij het optische centrum en de belangrijkste focus, die we al hebben opgemerkt die is weergegeven met de letter F.

Kan u van dienst zijn: ton: transformaties, gelijkwaardigheid en oefeningen opgelost

Het wordt de belangrijkste focus genoemd tot het punt waar alle stralen die de lens parallel aan de hoofdas beïnvloeden, worden gevonden.

De afstand tussen het optische centrum en de focus wordt focale afstand genoemd.

De centra van kromming worden gedefinieerd als de centra van de bollen die de lens creëren; Aan de andere kant zijn de radio's van kromming de radio's van de bollen die aanleiding geven tot de lens.

En ten slotte wordt het optisch vlak genoemd naar het centrale vlak van de lens.

Afbeeldingen vorming in convergente lenzen

In het licht van de vorming van afbeeldingen in convergente lenzen, moet een reeks basisregels die hieronder worden uitgelegd, in aanmerking worden genomen.

Als de straal de lens parallel aan de as beïnvloedt, convergeert de opkomende straal in het focusbeeld. Omgekeerd, als een invallende straal de objectfocus kruist, verschijnt bliksem in een richting parallel aan de as. Ten slotte worden de stralen die het optische centrum oversteken, gebroken zonder een afwijking te ervaren.

Als gevolg hiervan kunt u in een convergente lens de volgende situaties geven:

- Dat het object zich bevindt ten opzichte van het optische vlak op een afstand groter dan het dubbele van de brandpuntsafstand. In dat geval is de afbeelding die zich voordoet echt, omgekeerd en kleiner dan het object.

- Dat het object zich op een afstand van het optische vlak bevindt gelijk aan twee keer de focale afstand. Wanneer dit gebeurt, is de verkregen afbeelding een echt, omgekeerde beeld en dezelfde grootte als het object.

- Dat het object zich op een afstand van het optische vlak tussen eenmaal en twee keer de focale afstand bevindt. Dus een afbeelding wordt geproduceerd, is echt, omgekeerd en groter dan het oorspronkelijke object.

- Dat het object zich op een afstand van het optische vlak lager bevindt dan de brandpuntsafstand. In dat geval zal de afbeelding virtueel, direct en groter zijn dan het object.

Kan u van dienst zijn: magnetische schok: eenheden, formules, berekening, voorbeelden

Soorten convergente lens

Er zijn drie verschillende soorten convergente lenzen: biconvex -lenzen, planoconvex -lenzen en concavoconvexlenzen.

Biconvex -lenzen zijn, zoals de naam al aangeeft, samengesteld uit twee convexe oppervlakken. Planoconvexas heeft ondertussen een plat oppervlak en een andere convex. En ten slotte worden concavoconvex -lenzen gevormd door een enigszins concaaf oppervlak en een andere bol.

Verschil met uiteenlopende lenzen

Convergente lens. FIR0002 (talk) (uploads) [CC BY-SA 3.0 (http: // creativeCommons.Org/licenties/by-sa/3.0/]]

Uit uiteenlopende lenzen verschillen daarentegen van de convergente in die zin dat de dikte afneemt van de randen naar het midden. Dus, in tegenstelling tot wat er met de convergent is gebeurd, in dit type lenzen de lichtstralen die de hoofdas parallel beïnvloeden. Op deze manier vormen ze wat virtuele afbeeldingen van objecten wordt genoemd.

In optica worden uiteenlopende of negatieve lenzen, zoals ze ook bekend zijn, voornamelijk gebruikt om bijziendheid te corrigeren.

Gauss -vergelijkingen van dunne lenzen en verhoogde lens

Over het algemeen zijn het type lenzen dat wordt bestudeerd dat dunne lenzen worden genoemd. Deze worden gedefinieerd als die met een kleine dikte in vergelijking met de kromming van de oppervlakken die hen beperken.

Dit type lens kan worden bestudeerd met de Gauss -vergelijking en met de vergelijking die het mogelijk maakt om de toename van een lens te bepalen.

Gauss -vergelijking

De Gauss -vergelijking van dunne lenzen dient om een ​​veelheid aan basisoptica -problemen op te lossen. Vandaar het grote belang ervan. Je uitdrukking is als volgt:

1/f = 1/P +1/Q

Waarbij 1/ f is wat de kracht van een lens wordt genoemd en f is de brandpuntsafstand of afstand van het optische centrum naar de focam. De meeteenheid van het vermogen van een lens is de diopter (d), zijnde 1 d = 1 m^-1. Van zijn deel zijn P en Q respectievelijk de afstand waarop een object en de afstand waarnaar het beeld wordt waargenomen.

Het kan u van dienst zijn: theorie van de oerknal: kenmerken, fasen, bewijs, problemen

Verhoogde lens

De laterale toename in een dunne lens wordt verkregen met de volgende uitdrukking:

M = - Q / P

Waar M de toename is. Uit de waarde van de toename kan een reeks gevolgen worden afgeleid:

JA | M | > 1, de grootte van de afbeelding is groter dan die van het object

JA | M | < 1, el tamaño de la imagen es menor que el del objeto

Als m> 0 is de afbeelding goed en aan dezelfde kant van de lens als het object (virtuele afbeelding)

Ja m < 0, la imagen está invertida y en el lado contrario que el objeto (imagen real)

Oefening opgelost

Een lichaam bevindt zich een meter verwijderd van een convergente lens, die een brandpuntsafstand van 0, 5 meter heeft. Hoe zal het beeld van het lichaam zijn? Hoe ver ga je vinden?

We hebben de volgende gegevens: p = 1 m; F = 0,5 m.

We vervangen deze waarden in de Gauss -vergelijking van de dunne lenzen:

1/f = 1/P +1/Q

En het volgende blijft:

1/0.5 = 1 + 1/q; 2 = 1 + 1/q

We wissen 1/q

1/Q = 1

Om vervolgens Q te wissen en te verkrijgen:

Q = 1

Van daaruit vervangen we in de vergelijking van de toename van een lens:

M = -q / p = -1 / 1 = -1

Daarom is de afbeelding echt sinds Q> 0, omgekeerd omdat m < 0 y de igual tamaño dado que el valor absoluto de M es 1. Por último, la imagen se encuentra a un metro de distancia del foco.

Referenties

1. Licht (n.D.)). In Wikipedia. Opgehaald op 18 maart 2019, hiervan.Wikipedia.borg.
2. Lekner, John (1987). Reflectietheorie, van elektromagnetische en particele golven. Springer.
3. Licht (n.D.)). In Wikipedia. Ontvangen op 20 maart 2019, van.Wikipedia.borg.
4. Lens (n.D.)). In Wikipedia. Opgehaald op 17 maart 2019, hiervan.Wikipedia.borg.
5. Lens (optica). In Wikipedia. Ontvangen op 19 maart 2019, van.Wikipedia.borg.
6. Acts, Eugene (2002). Optiek (4e ed.)). Addison Wesley.
7. Tupler, Paul Allen (1994). Fysiek. 3e editie. Barcelona: ik heb achteruit.