Wiskundige gelijkheid
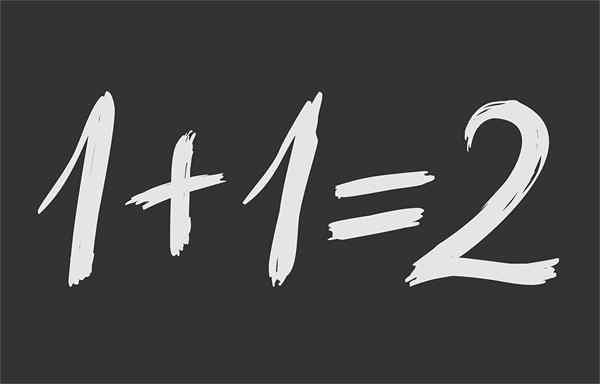
- 2504
- 526
- James Dach
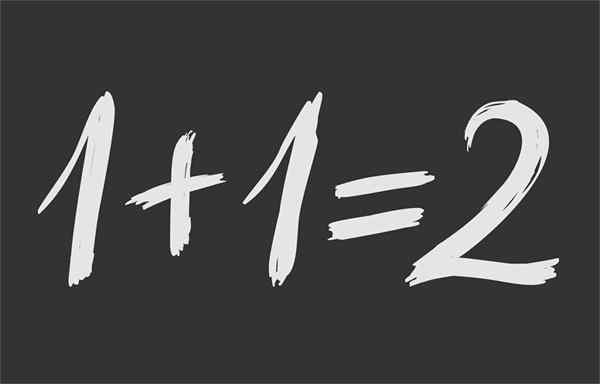 Figuur 1.- Wiskundige gelijkheid zorgt ervoor dat 1 + 1 hetzelfde is 2
Figuur 1.- Wiskundige gelijkheid zorgt ervoor dat 1 + 1 hetzelfde is 2 Wat is wiskundige gelijkheid?
Een wiskundige gelijkheid zorgt ervoor dat twee uitdrukkingen hetzelfde of verschillend zijn, ze zijn totaal equivalent. Deze uitdrukkingen kunnen een diverse aard zijn, bijvoorbeeld getallen, letters die hoeveelheden of grootten symboliseren, combinaties van getallen en letters, matrices en meer.
Het symbool dat wordt gebruikt om gelijkheid in wiskundige taal aan te duiden, is dat van twee parallelle en horizontale lijnen, die in gedrukte tekst het goed bekende symbool is "=". Als u bijvoorbeeld drie appels hebt, kunt u de volgende gelijkheid schrijven:
Aantal appels = 3
De uitdrukking "Aantal appels" is het lid van links en nummer 3 is het lid rechts van gelijkheid.
Omdat het mogelijk is om op verschillende manieren numerieke hoeveelheden te schrijven, wordt gelijkheid gebruikt om ze aan te duiden. Het nemen van een specifiek geval om het punt te illustreren, er zijn verschillende manieren om het nummer 4 te schrijven, afgezien van de meest voor de hand liggende die 4 = 4 is, kan het volgende worden geschreven, door een wiskundige gelijkheid:
2 + 2 = 4
6 - 2 = 4
8 ÷ 2 = 4
2 × 2 = 4
22 = 4
De hier getoonde gelijkheid is waar, maar een gelijkheid is misschien niet, bijvoorbeeld 10 + 5 = 20 is onwaar, omdat 10 + 5 = 15.
De lezer weet zeker andere manieren om nummer 4 te schrijven. Merk op dat uitdrukkingen aan elke kant van gelijkheid getallen, woorden, letters kunnen zijn die bedragen of andere symbolen symboliseren, bijvoorbeeld:
x + 1 = 7
naar2B - 1 = XY
f (x) = 2x2
Wiskundigen gebruikten niet altijd het gelijkheidssymbool, dus de oude wiskunde -verdragen waren zeer uitgebreid.
Het wordt toegeschreven aan de wiskundige en dokter Robert Remember (1510-1558), geboren in Wales, de creatie van het gelijkheidssymbool "=", zo bekend voor iedereen vandaag. Vergeet niet, blijkbaar moe van het schrijven van de uitdrukking "net als" in een van zijn wiskunde -verdragen, besloot hij om in zijn plaats de familieleden parallelle strepen af te kraven.
Kan u van dienst zijn: Pentagonal Prism: Kenmerken, onderdelen, hoekpunten, randen, volumeEigenschappen van wiskundige gelijkheid
De volgende eigenschappen laten correct werken met wiskundige gelijkheid. Ze zijn axiomatisch, dus ze vereisen geen demonstratie:
1.- Reflecterende eigenschap
Deze eigenschap stelt vast dat elk bedrag gelijk is aan zichzelf. In het bijzonder, aangezien elk getal gelijk is aan zichzelf, kunnen gelijke kunnen worden geschreven:
5 = 5
36.35 = 36.35
Als een bedrag letterlijk is, of het is een combinatie van letters en getallen, is het ook gelijk aan zichzelf:
3x = 3x
naar2BC-1 = A2BC-1
2.- Eigenschap van symmetrie
De bedragen of leden aan beide zijden van gelijkheid kunnen worden uitgewisseld zonder verloren geldigheid. Dat wil zeggen, als wat links van het "=" -symbool is geschreven aan uw rechterkant, en wat aan uw rechterkant is, wordt links geplaatst, het is dezelfde gelijkheid.
Expressie 5 + 2 = 7 is bijvoorbeeld gelijk aan deze: 7 = 5 + 2. Op dezelfde manier:
12 + 8 = 20; 20 = 12 + 8
x + 1 = 3; 3 = x + 1
x - z = y; y = x - z
3.- Transitieve eigenschap
Deze eigenschap verwijst naar de gelijkwaardigheid van gelijkheid. Als twee gelijkheid een gemeenschappelijk lid heeft, zijn ze ook hetzelfde, sinds over het algemeen:
Als "x = y" en "y = z" dan x = z
Overweeg deze twee numerieke gelijkheden om deze eigenschap te illustreren: 2 + 2 = 4 en 6 - 2 = 4. Omdat beide gelijk zijn aan 4 (ze hebben een gemeenschappelijk lid), kan het volgende worden geschreven, zonder enige geldigheid te verliezen:
2 + 2 = 6 - 2
Een ander voorbeeld, deze keer met letters:
Ja x + 1 = 5
EN
A - B = 5
Dus:
x+1 = a - b
4.- Annuleringseigenschap
Een gelijkheid wordt niet gewijzigd als bij beide leden hetzelfde bedrag is dat toevoegt (of aftrekt) en er wordt besloten dit te elimineren of te annuleren. Dit is de annuleringseigenschap van de som.
Neem als voorbeeld de volgende numerieke gelijkheid waarin de 10 zowel in het lid van rechts als in die links verschijnt:
Het kan u van dienst zijn: Trigonometrische functies: Basic, in het Cartesiaanse vlak, voorbeelden, oefening2 + 2 + 10 = 6 - 2 + 10
Het nummer 10 kan worden geannuleerd zonder gelijkheid die zijn geldigheid verliest, waardoor een andere kortere gelijkheid en gelijkwaardig is aan de vorige:
2 + 2 = 6 - 2
In gelijkheid (10 ÷ 2) - 3 = 5 - 3 Het gehele getal - 3 behoort tot beide leden van gelijkheid en verschijnt als toevoeging, daarom kan worden geannuleerd, verkrijgen:
10 ÷ 2 = 5
Het gebeurt ook met letterlijke hoeveelheden, bijvoorbeeld:
Ja x + 2y + z = −a + b + z
Dan kan de "Z" worden geannuleerd, omdat deze aan beide zijden van gelijkheid wordt gevonden als toevoeging (en met hetzelfde teken).
Daarbij resulteert het:
x + 2y = −a + b
Het kan ook de annuleringseigenschap van vermenigvuldiging definiëren. Als hetzelfde bedrag C beide leden van gelijkheid vermenigvuldigt, kan dit bedrag bijvoorbeeld worden geannuleerd:
Cx = cy
Dan kan C worden geannuleerd om eenvoudig te verkrijgen:
x = y
5.- Uniformiteitseigenschap
Een gelijkheid blijft onveranderlijk door toe te voegen, af te trekken, te vermenigvuldigen of te delen door dezelfde hoeveelheid aan beide zijden van hetzelfde.
Het moet bijvoorbeeld tot 8 + 5 = 13, als beide leden zich vermenigvuldigen met een bepaald willekeurig nummer C = 2, blijft gelijkheid bestaan:
(8+5) × 2 = 13 × 2
13 × 2 = 26
Wiskundige gelijke klassen
Er zijn verschillende soorten wiskundige gelijkheid, dus ze zijn geclassificeerd voor hun beste begrip in:
-Identiteit, Ze zijn gelijkheid waarin beide leden identiek zijn:
2 = 2
x = x
2x = x + x
enzovoort.
-Vergelijkingen, Dit zijn gelijkeheden waarin een of meer onbekenden verschijnen en waar zijn voor bepaalde waarden, dat wil zeggen, gelijkheid wordt niet gehaald voor enige willekeurige waarde, dus ze zijn ook bekend als bekend als Voorwaardelijke gelijkheden. Voorbeelden:
x + 1 = 5
X3 = 27
A + B = 40
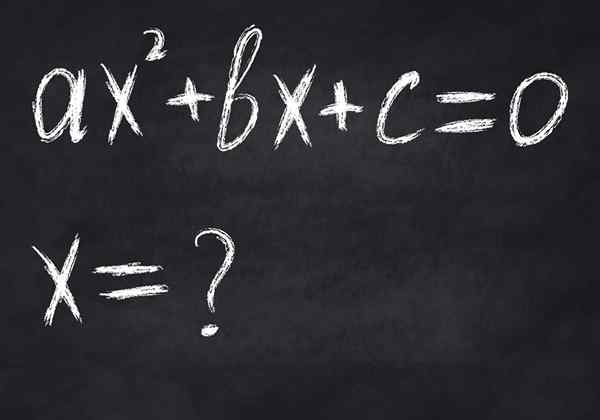 Figuur 2.- Een vergelijking is een voorwaardelijke wiskundige gelijkheid, omdat deze alleen wordt voldaan voor bepaalde variabele waarden. De afbeelding toont een tweede graad vergelijking, die maximaal twee echte oplossingen heeft
Figuur 2.- Een vergelijking is een voorwaardelijke wiskundige gelijkheid, omdat deze alleen wordt voldaan voor bepaalde variabele waarden. De afbeelding toont een tweede graad vergelijking, die maximaal twee echte oplossingen heeft -Gelijkwaardigheid, In hen is het lid van links gelijk aan de rechterkant aan de rechterkant, zelfs als ze niet gelijk zijn, bijvoorbeeld in: 23 = 8.
Kan u van dienst zijn: additief principe-Formules, Het is een gelijkheid die altijd wordt vervuld voor de waarden van de onafhankelijke variabele, zoals in de goed bekende formule voor de afstand D, afhankelijk van de tijd T van een mobiel met uniforme rechtlijnige beweging: D = v ∙ t
Opgeloste oefeningen
Oefening 1
Schrijf het nummer 10 tot en met vier verschillende en equivalente gelijkheid.
Oplossing
Al deze gelijkheid drukken nummer 10 uit, maar op verschillende manieren:
5 × 2 = 10
11-1 = 10
101= 10
20 ÷ 2 = 10
Oefening 2
Wat is de waarde van x die voldoet aan gelijkheid x + 1 = 3?
Oplossing
Deze gelijkheid is een vergelijking, omdat de waarde van X onbekend is. Eigenschap 5 gebruiken, als de expressie x + 1 = 3 wordt toegevoegd (−1) aan beide zijden van het symbool "=", blijft gelijkheid bestaan:
x + 1 + (−1) = 3 + ( - 1)
Bij het toevoegen van (−1) aan het lid van links en de bewerking is opgelost, is de "x" alleen aan de linkerkant van gelijkheid, deze procedure wordt genoemd goedkeuring:
x + 1 - 1 = 3−1
x = 2
Daarom is de waarde die voldoet aan deze gelijkheid x = 2.
Oefening 3
Als een mobiel met uniforme rechtlijnige beweging een snelheid van 2 heeft.5 m/s, wat is de afstand die na 3 seconden loopt?
Oplossing
De formule die in de vorige sectie wordt gezien, wordt gebruikt, D = v ∙ t, waarin de waarde van V wordt vervangen:
D = 2.5 ∙ t
De uitdrukking wordt een gelijkheid wanneer t = 3 seconden en de bewerking wordt opgelost:
D = 2.5 ∙ 3 m = 7.5m
Wat resulteert in gelijkheid:
D = 7.5m
Referenties
- Barnett, r. 20000000000000000000. Vóór de sculptuur. 4e. Editie. McGraw Hill.
- Larson, r. 2012. Vóór de sculptuur. 8e. Editie. Cengage leren.
- Pérez, V. Eigenschappen van algebraïsche gelijkheid. Hersteld van: wiskunde.Laguia2000.com.
- Eigenschappen van gelijkheid. Opgehaald uit: PPS.K12.Of.ons.
- Stewart, J. 2007. Pre-berekening: wiskunde voor berekening. 5e. Editie. Cengage leren.

