Pythagorische identiteiten demonstratie, bijvoorbeeld oefeningen

Zijn Pythagorische identiteiten Alle trigonometrische vergelijkingen waaraan wordt voldaan voor elke waarde van de hoek en zijn gebaseerd op de stelling van Pythagoras. De beroemdste van Pythagorese identiteiten is de fundamentele trigonometrische identiteit:

Sen²(α) + cos²(α) = 1

Figuur 1. Pythagorische trigonometrische identiteiten.

Het is nog steeds in belang en gebruikt de Pythagorese identiteit van de raaklijn en de Secant:

Dus²(α) + 1 = sec²(α)

En de Pythagorese trigonometrische identiteit waarbij de cotangent en de oogstster betrokken is:

1 + CTG²(α) = CSC²(α)

[TOC]

Demonstratie

De trigonometrische redenen borst En cosinus Ze worden weergegeven in een straalomtrek één (1) bekend als trigonometrische cirkel. Deze cirkel heeft een centrum bij de oorsprong van coördinaten of.

De hoeken worden gemeten vanuit de positieve semi -as van de X, bijvoorbeeld de hoek α in figuur 2 (zie later). In tegenstelling tot de klokken als de hoek positief is, en in de richting van de handen als het een negatieve hoek is.

De semi -recht met oorsprong of en hoek α wordt getekend, die de eenheidscirkel onderschept op punt P. Punt P wordt orthogonaal geprojecteerd op de horizontale as x die aanleiding geeft tot punt C. Evenzo wordt P loodrecht geprojecteerd op de verticale as en geeft aanleiding tot punt S.

Je hebt de juiste OCP -driehoek in C. 

De borst en de cosinus

Er moet aan worden herinnerd borst Het wordt als volgt op een rechter driehoek gedefinieerd:

De boezem van een hoek van de driehoek is de verhouding of verhouding tussen de cateto die tegen de hoek en de hypotenusa van de driehoek is.

Toegepast op de OCP -driehoek van figuur 2 zou zo zijn:

Sin (α) = cp / op

Maar CP = OS en OP = 1, dus dat:

Sin (α) = os

Wat betekent dat de projectie op de y -as een waarde heeft die gelijk is aan de boezem van de getoonde hoek. Opgemerkt moet worden dat de maximale waarde van de borst van een hoek (+1) optreedt wanneer α = 90º en het minimum (-1) wanneer α = -90º of α = 270º.

Kan u van dienst zijn: Vector Space: Base en Dimension, Axioms, Properties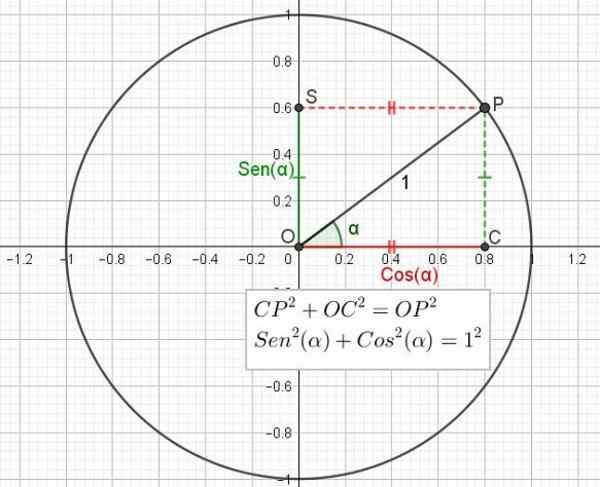Figuur 2. Trigonometrische cirkel toont de relatie tussen Pythagoras Stelling en fundamentele trigonometrische identiteit. (Eigen uitwerking)

Evenzo is de cosinus van een hoek de verhouding tussen de categorie grenzend aan de hoek en de hypotenusa van de driehoek.

Toegepast op de OCP -driehoek van figuur 2 zou zo zijn:

Cos (α) = oc / op

Maar op = 1, dus dat:

Cos (α) = oc

Wat betekent dat de OC -projectie op de X -as een waarde heeft die gelijk is aan die van de boezem van de getoonde hoek. Opgemerkt moet worden dat de maximale waarde van de cosinus (+1) optreedt wanneer α = 0º of α = 360º, terwijl de minimale waarde van de cosinus (-1) is wanneer α = 180º is.

De fundamentele identiteit

Voor de rechthoek OCP -driehoek wordt de Pythagoras -stelling toegepast, waarin staat dat de som van het kwadraat van de categorieën gelijk is aan het kwadraat van de hypotenuse:

CP² + OC² = OP²

Maar er is al gezegd dat CP = OS = sin (α), dat oc = cos (α) en dat op = 1, dus de vorige uitdrukking kan worden herschreven, afhankelijk van de sinus en cosinus van de hoek:

Sen²(α) + cos²(α) = 1

De raaklijn

Net zoals de x -as in de trigonometrische cirkel de as van de cosinus en de as en de as van de borst is, is er op dezelfde manier de as van de raaklijn (zie figuur 3) die precies de lijn is die naar de eenheid raakt cirkel op het punt op het punt B -coördinaat (1, 0). 

Als u de waarde van de raaklijn van een hoek wilt weten, wordt de hoek getrokken uit de positieve semi -as van de X, de snijpunt van de hoek met de as van de raaklijn definieert een punt Q, de lengte van het OQ -segment is de raaklijn van de hoek.

Kan u van dienst zijn: algebraïsche derivaten

Dit komt omdat per definitie de raaklijn van hoek α de tegenovergestelde cateto qb is tussen de aangrenzende cateto OB. Dat wil zeggen dit (α) = qb / ob = qb / 1 = qb.

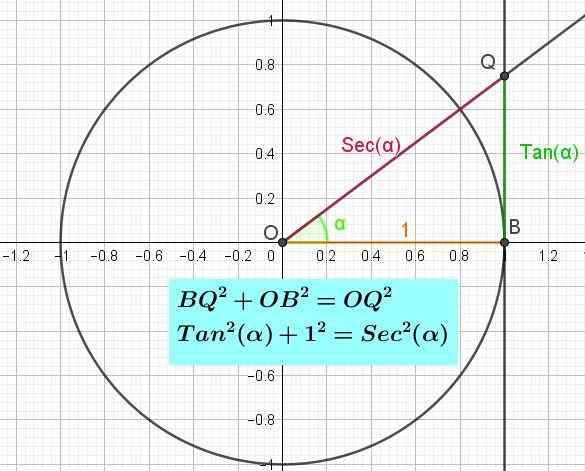figuur 3. De trigonometrische cirkel toont de as van de raaklijn en de Pythagoras -identiteit van de raaklijn. (Eigen uitwerking)

De Pythagorische identiteit van de raaklijn

De Pythagorese identiteit van de raaklijn kan worden aangetoond als de rechthoek driehoek in B (figuur 3) wordt overwogen (figuur 3). Het toepassen van de Pythagoras -stelling op die driehoek die u moet bq² + OB² = OQ². Maar er is al gezegd dat BQ = tan (α), die ob = 1 en dat oq = sec (α), zodat die vervanging in de gelijkheid van pythagoras voor de juiste driehoek obq heeft:

Dus²(α) + 1 = sec²(α).

Voorbeeld

Controleer of Pythagorese identiteiten al dan niet worden voldaan in de rechthoekige driehoek van cateto's AB = 4 en BC = 3.

Oplossing: de categorieën zijn bekend, het is noodzakelijk om de hypotenuse te bepalen, namelijk:

Ac = √ (ab^2 + bc^2) = √ (4^2 + 3^2) = √ (16 + 9) = √ (25) = 5.

De hoek ∡bac wordt α, ∡bac = α genoemd. Nu worden de trigonometrische redenen bepaald:

Sin α = bc / ac = 3/5 

Cos α = ab / ac = 4/5 

Tan α = bc / ab = 3/4 

Cotan α = ab / bc = 4/3 

SEC α = AC / AB = 5/4 

CSC α = AC / BC = 5/3

Het begint met een fundamentele trigonometrische identiteit:

Sen²(α) + cos²(α) = 1

(3/5)^2 + (4/5)^2 = 9/25 + 16/25 = (9 +16)/25 = 25/25 = 1

Er wordt geconcludeerd dat het is vervuld.

- De volgende Pythagorische identiteit is die van de raaklijn:

Dus²(α) + 1 = sec²(α)

(3/4)^2 + 1 = 9/16 + 16/16 = (9 + 16)/16 = 25/16 = (5/4)^2

En er wordt geconcludeerd dat de identiteit van de raaklijn wordt geverifieerd.

- Evenzo die van de cotangent:

Kan u van dienst zijn: willekeurige selecties met of zonder vervanging

1 + CTG²(α) = CSC²(α)

1+ (4/3)^2 = 1 + 16/9 = 25/9 = (5/3)^2

Er wordt geconcludeerd dat het ook is vervuld, dat de taak heeft voltooid om de Pythagoras -identiteiten voor de gegeven driehoek te verifiëren.

Opgeloste oefeningen

Test de volgende identiteiten, gebaseerd op de definities van trigonometrische redenen en pytagorische identiteiten.

Oefening 1

Bewijs wat COS² x = (1 + sen x) (1 - sin x).

Oplossing: Het juiste lid herkent het opmerkelijke product van de vermenigvuldiging van een binomiaal door zijn conjugaat dat, zoals bekend, een verschil is van vierkanten:

Zomaar² x = 1² - Sen² X

Dan gaat de term met borst aan de rechterkant naar de linkerkant met het gewijzigde bord:

Zomaar² X + sen² x = 1

Opmerking dat de fundamentele trigonometrische identiteit is bereikt, dus wordt geconcludeerd dat de gegeven uitdrukking een identiteit is, dat wil zeggen dat deze wordt vervuld voor elke waarde van x.

Oefening 2

Beginnend met de fundamentele trigonometrische identiteit en het gebruik van de definities van trigonometrische redenen om de Pythagoras -identiteit van de Harvester aan te tonen.

Oplossing: de fundamentele identiteit is:

Sen²(x) + cos²(x) = 1

Beide leden zijn verdeeld tussen sen²(x) en de noemer wordt verdeeld in het eerste lid:

Sen²(x)/sin²(x) + cos²(x)/sin²(x) = 1/sen²(X)

Het is vereenvoudigd:

1 + (cos (x)/sen (x))^2 = (1/sin (x))^2

Cos (x)/sin (x) = cotan (x) is een identiteit (niet -pythagoras) die wordt geverifieerd door de definitie van trigonometrische redenen. Op dezelfde manier gebeurt het met de volgende identiteit: 1/sin (x) = csc (x).

Eindelijk moet je:

1 + CTG²(x) = CSC²(X)

Referenties

1. Baldor J. (1973). Vlakke geometrie en ruimte met een inleiding tot trigonometrie. Midden -Amerikaans cultureel. C.NAAR.
2. C. EN. NAAR. (2003). Geometrie -elementen: met oefeningen en kompasgeometrie. Universiteit van Medellin.
3. Campos, f., Cerecedo, f. J. (2014). Wiskunde 2. Patria -redactiegroep.
4. Iger. (S.F.)). Wiskunde eerste semester Tacaná. Iger.
5. Jr. Geometrie. (2014). Polygonen. Lulu Press, Inc.
6. Miller, Heeren, & Hornsby. (2006). Wiskunde: redeneren en applicaties (tiende editie). Pearson Education.
7. Patiño, m. (2006). Wiskunde 5. Redactionele progreso.
8. Wikipedia. Trigonometrie -identiteiten en formules. Hersteld van: is.Wikipedia.com