Wiskunde

Hyperbool

2119
393
Hugo Crooks

Wat is een hyperbool?

De hyperbool is de reeks punten van het vlak zodanig dat de absolute waarde van het verschil tussen de afstanden tot twee vaste punten, Spotlights genoemd, constant blijft. Deze set punten vormt de curve met twee takken waargenomen in figuur 1.

Er is een punt p (x, y), de focus f₁ en f₂ gescheiden een afstand gelijk aan 2c. De wiskundige manier om deze relatie uit te drukken is door:

$\left |d__P_1-d__P_2 \right |=constante$

Figuur 1. Hyperbool met horizontale focusas. Bron: f. Zapata.

Alle punten van de hyperbool voldoen aan deze voorwaarde, die leidt tot de hyperboolvergelijking, zoals later zal worden gezien. Het middelpunt tussen de schijnwerpers wordt midden C genoemd en in de figuur valt het samen met het punt (0,0), maar de hyperbool kan ook worden verplaatst en het midden komt overeen met een ander coördinaatpunt C (h, k).

In de bovenste figuur is de X -as de focale as van de hyperbool, omdat er de schijnwerpers zijn, maar je kunt er ook een bouwen waarvan de focale as de as en as is.

De hyperbool maakt deel uit van de krommen die bekend staan conisch, Ze worden dat genoemd omdat ze kunnen worden afgeleid van de snede van een kegel met een platte gedeelte. Een hyperbool wordt verkregen bij het kruisen van de kegel en het vlak, op voorwaarde dat deze niet door het hoekpunt van de kegel gaat en de hoek die het vlak vormt met de as van de kegel is minder dan degene die vormt met de generatrix -as van de dezelfde.

Samen met de gelijkenis, omtrek en ellips zijn conische stoffen bekend sinds de oude tijden. De Griekse wiskundige Apollonius van Perga (262-190 v.Chr.) Schreef een geometrieverdrag waar hij zijn eigendommen beschreef en hij gaf hen zelf de namen waarmee ze elkaar tot vandaag kennen.

Kenmerken van de hyperbool

Dit zijn enkele van de meest opvallende kenmerken van een hyperbool:

Het is een platte curve, daarom is het voldoende om de coördinaten (x, y) van elk punt dat erbij hoort te geven.
Het is ook een open curve, in tegenstelling tot de omtrek of ellips.
Het heeft twee takken symmetrisch gerangschikt.
Zowel de verticale as als de horizontale as kunnen worden beschouwd als symmetrie -assen, maar de as waar de schijnwerpers worden genoemd focale as of hoofdas.
Het is symmetrisch ten opzichte van het centrum.
De hyperbool snijdt de focale as op twee punten genoemd Hoekpunten, Daarom wordt de focale as soms genoemd Echte as, Terwijl de andere as wordt genoemd Denkbeeldige as, Omdat het geen punten gemeen heeft met de hyperbool.
Het midden van de hyperbool bevindt zich halverwege tussen de punten die Foci worden genoemd.
Het wordt geassocieerd met twee zeer specifieke lijnen die asymptoten worden genoemd, die lijnen zijn waaraan de hyperbool nadert, maar zonder ze te kruisen, wanneer de waarden van x e y erg groot zijn. De asymptoten kruisen elkaar in het midden van de hyperbool.

Kan u van dienst zijn: overjectieffunctie: definitie, eigenschappen, voorbeelden

Vergelijkingen en formules

Hiperbol -vergelijking met centrum in (0.0)

Beginnend met de definitie in het begin:

$\left |d__P_1-d__P_2 \right |=constante$

Tot deze positieve constante wordt het meestal 2A genoemd en het is de afstand die de hoekpunten van de hyperbool scheidt, dan:

$\left |d__P_1-d__P_2 \right |=2a$

Aan de andere kant, DP₁, Dp₂ en 2c zijn de zijden van de driehoek getoond in figuur 1, en door elementaire geometrie is de aftrekking van de vierkanten van de zijkanten van een driehoek altijd minder dan het vierkant van de resterende zijde. Dus:

4e²< 4c²

EN:

naar < c

Dit resultaat zal binnenkort nuttig zijn.

Als de afstand tussen twee punten P₁(X₁,En₁) En P₂(X₂,En₂) is:

$d_12=\sqrt(x_2-x_1)^2+(y_2-y_1)^2$

Door coördinaten P (x, y) te vervangen, f₁(-C, 0) en f₂(C, 0) Het blijft:

$\left |d_P_1-d_P_2 \right |=\left |\sqrt(x+c)^2+(y-0)^2-\sqrt(x-c)^2+(y-0)^2 \right |=2a$

Die gelijkwaardig is aan:

$\sqrt(x+c)^2+(y-0)^2-\sqrt(x-c)^2+(y-0)^2=\pm 2a$

Vierkant in beide leden om de wortels te elimineren en de termen die u bereikt te reorganiseren:

$\left (c^2-a^2 \right )x^2-a^2 y^2 =\left (c^2-a^2 \right )a^2$

Naar kwantiteit C² - naar², wat altijd een positief bedrag is omdat < c, se la denomina b², Daarom wordt het bovenstaande herschreven als:

B²X² - naar²En² = A² B²

Alle termen verdelen door² B², Het is de hyperboolvergelijking gecentreerd op (0,0) met de horizontale echte as:

$\fracx^2a^^2-\fracy^2b^^2=1$

Met a en b groter dan 0. Deze vergelijking wordt genoemd Hyerbola -canonieke vergelijking en de noemer van² Het komt altijd overeen met de positieve fractie.

De hyperbool gecentreerd op (0,0) en met de echte as verticaal neemt de vorm aan:

$\fracy^^2a^2-\fracx^^2b^2=1$ Kruispunten van de hyperbool met de coördinaatassen

De kruispunten van de hyperbool met de coördinaatassen worden respectievelijk gedaan y = 0 en x = 0 in de vergelijking:

Voor y = 0

X² /naar² = 1 ⇒ x² = A²

x = ± a

De hyperbool snijdt naar de x -as in twee punten genaamd hoekpunten, waarvan de respectieve coördinaten x zijn: x = a y x = -a

Voor x = 0

Het wordt verkregen -en² /B² = 1, die geen echte oplossing heeft en volgt dat de hyperbool niet naar de verticale as snijdt.

Hyperboolvergelijking met centrum in (H, K)

Als het midden van de hyperbool op punt C (H, K) staat, dan is de canonieke vergelijking ervan:

$\frac\left (x-h \right )^2a^^2-\frac\left (y-k \right )^2b^^2=1$

Hiperbola -elementen

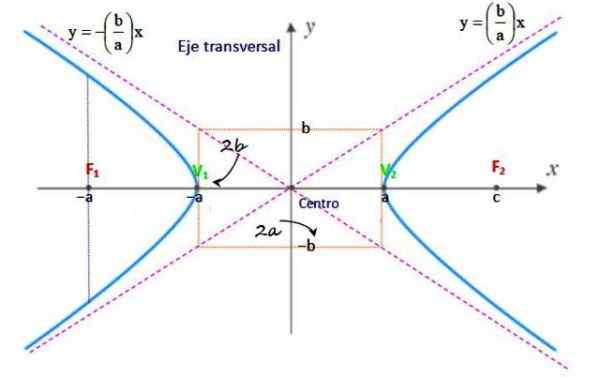Figuur 2. Hiperbola -elementen. Bron: f. Zapata.

Centrum

Het is het middelpunt van segment f₁F₂En de coördinaten zijn (h, k) of (x_of,En_of)).

Kan u van dienst zijn: synthetische verdeling

Focus

Het zijn de twee vaste punten f₁ en f₂ die zich op de echte as van de hyperbool bevinden, met betrekking tot welke het verschil van afstanden om P (x, y) te punt zijn, blijft constant. De afstand tussen de schijnwerpers en het midden van de hyperbool is "C".

Vectorradio

Dit wordt de afstand genoemd tussen een punt P en een van de schijnwerpers.

Focusafstand

Het is de afstand die beide schijnwerpers scheidt en gelijkwaardig is aan 2c.

Hoekpunten

De hoekpunten v₁ en v₂ Het zijn de punten waar de hyperbool de echte as kruist. Een hoekpunt en het midden van de hyperbool worden gescheiden door afstand A, daarom is de afstand tussen de hoekpunten 2A.

Focale as, hoofdas of echte as

Het is de as waar de schijnwerpers zich bevinden en meet 2c. Het kan zich op een van de twee Cartesiaanse assen bevinden en de hyperbool kruist het op de punten die hoektjes worden genoemd.

Transversale as, secundaire as of denkbeeldige as

Het is de as loodrecht op de focale as en meet 2B. De hyperbool snijdt het niet, dus het wordt ook een denkbeeldige as genoemd.

Asymptoten

Het zijn twee lijnen, waarvan de respectieve hangende zijn m₁ = (b/a) en m₂ = - (b/a), die bedoeld zijn in het midden van de hyperbool. De curve snijdt deze lijnen nooit en het product tussen de afstanden van enig punt van de hyperbool tot de asymptoten, het is constant.

Om de vergelijkingen van de asymptoten te vinden, matchen gewoon de linkerkant van de hyperboolcanonieke vergelijking met 0. Bijvoorbeeld voor hyperbool gecentreerd op oorsprong:

$\fracx^^2a^2-\fracy^^2b^2=0\Rightarrow \fracy^^2b^2=\fracx^^2a^2$

Hyberbola -rechthoek

Het is de rechthoek waarvan de breedte de afstand is tussen hoekpunten 2a en afstand 2B en is gericht op het midden van de hyperbool. De constructie vergemakkelijkt de handmatige indeling van de hyperbool.

Rechte kant

Touw dat door een van de schijnwerpers gaat, loodrecht op de echte as.

Excentriciteit

Het wordt gedefinieerd als het quotiënt tussen de brandpuntsafstand en de echte as:

E = c/a

Het is altijd groter dan 1, omdat C groter is dan A en minder dan √2.

De waarde van en geeft aan of de hyperbool tamelijk gesloten is (smalle rechthoek, langwerpig in de richting van de hoofdas) of open (brede rechthoek, langwerpig in de richting van de denkbeeldige as).

Rechte raaklijn naar hyperbool op punt P (x₁,En₁))

Een raaklijnlijn naar de hyperbool op een punt P (x₁,En₁) Het is de bissector van de twee radio -vectoren van dat punt.

Voor een hyperbool met de hoofdas parallel aan de X -as, raakt de helling van de lijn op de hyperbool op een punt P (x₁,En₁) is gegeven door:

Kan u van dienst zijn: gecombineerde bewerkingen

$m=\left (\fracba \right )^2\left (\fracx_1y_1 \right )$

En als de hyperbool de hoofdas is parallel aan de y -as, dan:

$m=\left (\fracab \right )^2\left (\fracx_1y_1 \right )$

Voorbeelden van hyperbool

Dispersie van alfa -deeltjes door een kern

Door atomaire kernen te bombarderen met alfa -deeltjes, die niets anders zijn dan heliumkernen, worden deze afgestoten, omdat elke atoomkern een positieve lading heeft. Deze heliumkernen zijn gedispergeerd na hyperbolische trajecten.

Trajecten van het zonnestelsellichamen

Figuur 3: Planeten van het zonnestelsel

In het zonnestelsel bewegen objecten onder de werking van de zwaartekracht. De beschrijving van de beweging komt voort uit een differentiaalvergelijking waarin de kracht conservatief is en omgekeerd evenredig met het kwadraat van de afstand. En de oplossingen van deze vergelijking zijn de mogelijke trajecten die de objecten volgen.

Welnu, deze trajecten zijn altijd conisch: omtrek, ellipsen, gelijkenissen of hyperbolen. De eerste twee zijn gesloten krommen, en dit is hoe de planeten bewegen, maar sommige kometen zijn nog steeds open trajecten, zoals gelijkenissen of hyperbolen, met de zon in een van de schijnwerpers.

Minimaal geluid

Wanneer er twee geluidsbronnen zijn, zoals twee luidsprekers die gelijkmatig in alle richtingen uitzenden, gelegen langs een rechte lijn, zijn de minima van geluidsintensiteit (destructieve interferentie) op een hyperbool waarvan de hoofdas wordt gezegd, en in de schijnwerpers van De hyperbool zijn de sprekers.

Oefening opgelost

Vind de elementen van de volgende hyperbool: hoekpunten, foci en asymptoten van de hyperbool en bouw de grafiek:

$\fracx^^216-\fracy^^24=1$

Oplossing

Het midden van deze hyperbool valt samen met de oorsprong van de coördinaten en de echte as is horizontaal, omdat de positieve fractie overeenkomt met variabele x.

De hyperbool semi -assen zijn:

naar² = 16 ⇒ A = 4

B² = 4 ⇒ B = 2

Op deze manier meet de centrale rechthoek 4 eenheden breed en 2 eenheden hoog. Herinnerend dat hierboven werd vermeld dat C² - naar²= B², Dus:

C² = A²+ B² ⇒ C² = 16 + 4 = 20

Daarom is focale semi-dienst:

C = √20 = 2√5

En de foci zijn op coördinaatpunten f₁ (-2√5.0) en f₂ (2√5.0).

De hellingen van de asymptotes zijn:

m = ± (b/a) = ± (2/4) = ± 0.5

Daarom zijn de respectieve vergelijkingen van elk:

En₁ = 0.5x; En₂ = -0.5x

Hyperbola kan eenvoudig grafiek maken via online software zoals Geogebra:

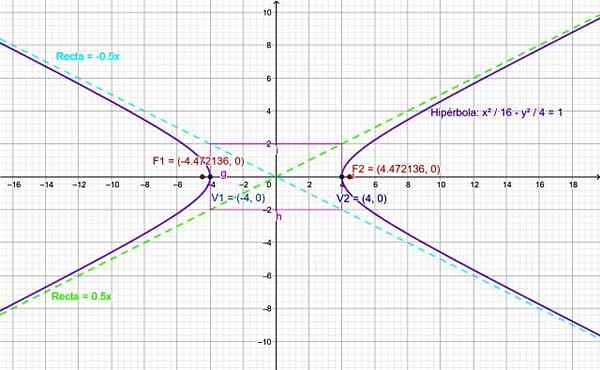Figuur 4. Grafiek voor de hyperbool van de oefening opgelost. Bron: f. Zapata.

Referenties