Transcendente functies typen, definitie, eigenschappen, voorbeelden

De transcendente functies Elementalen zijn exponentieel, logaritmische, trigonometrische, omgekeerde trigonometrische functies, hyperbolische en inverse hyperbolisch. Dat wil zeggen, het zijn die die niet kunnen worden uitgedrukt door een polynoom, een polynoom- of polynoomwortelsverhouding. 

De niet-elementaire transcendente functies staan ​​ook bekend als speciale functies en onder hen kan de foutfunctie worden genoemd. De algebraïsche functies (polynomen, polynomiale quotiënten en polynoomwortels) naast de transcendente functies Elementalen vormen wat in de wiskunde bekend staat als Elementaire functies.

Het wordt ook beschouwd als transcendente functies die het gevolg zijn van bewerkingen tussen transcendente functies of tussen transcendente en algebraïsche functies. Deze bewerkingen zijn: de som en het verschil in functies, product en verhouding van functies, evenals de samenstelling van twee of meer functies.

[TOC]

Definitie en eigenschappen

Exponentiële functie

Het is een echte functie van de echte onafhankelijke variabele van de vorm:

f (x) = a^x = a^X

waar naar Het is een positief reëel getal (A> 0) opgelost genaamd de basis. Circumflejo of supervisie worden gebruikt om de potentiëring aan te duiden.

Laten we in het geval dat A = 2 Dan is de functie als volgt:

f (x) = 2^x = 2^X

Die zal worden geëvalueerd voor verschillende waarden van de onafhankelijke variabele x:

Hieronder is een afbeelding waarbij de exponentiële functie voor verschillende basiswaarden wordt weergegeven, inclusief de basis En (NEPER -nummer En ≃ 2.72). Baseren En Het is zo belangrijk dat je over het algemeen over de exponentiële functie hebt, denk je aan E^x, dat wordt ook aangegeven exp (x).

Figuur 1. Exponentiële functie a^x, voor verschillende waarden van de basis a. (Eigen uitwerking)

Exponentiële functie -eigenschappen

Uit figuur 1 is te zien dat het domein van exponentiële functies reële getallen zijn (Dom F = R) en het bereik of de route zijn de positieve reële (liep f = R⁺)). 

Kan u van dienst zijn: symmetrie

Aan de andere kant gaan alle exponentiële functies, ongeacht de waarde van basis A, door het punt (0, 1) en op punt (1, a). 

Wanneer de basis A> 1, Dan groeit de functie en wanneer 0 < a < 1 De functie neemt af. 

De bochten van y = a^x en van y = (1/a)^x  Ze zijn symmetrisch ten opzichte van de as EN. 

Met uitzondering van de zaak A = 1, De exponentiële functie is injectief, dat wil zeggen, met elke waarde van de afbeelding, komt men overeen en alleen een startwaarde.

Logaritmische functie

Het is een echte werkelijke functie van reële onafhankelijke variabele op basis van de definitie van de logaritme van een nummer. Logaritme gebaseerd naar van een nummer X, Het is het nummer En waarnaar de basis moet worden verhoogd om het argument te verkrijgen X:

aanroepen_naar(x) = y ⇔ a^y = x

Dat is de Logaritm -functie in basis naar Het is de omgekeerde functie voor de exponentiële functie op basis van naar.

Bijvoorbeeld:

aanroepen₂1 = 0, omdat 2^0 = 1

Een ander geval, logboek₂4 = 2, omdat 2^2 = 4

De root logaritm van 2 is log₂√2 = ½, omdat 2^½ = √2

aanroepen₂ ¼ = -2, in het oog dat 2^(-2) = ¼ 

Hieronder is een grafiek van de logaritm -functie in verschillende bases.

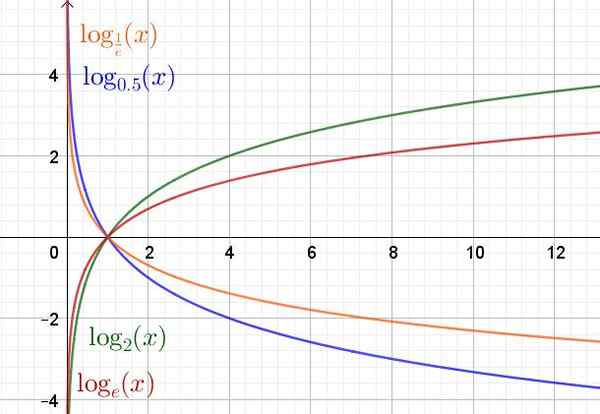Figuur 2. Exponentiële functie voor verschillende basiswaarden. (Eigen uitwerking)

Logaritmo -functie -eigenschappen

Het domein van de logaritm -functie en (x) = lognaar(X)  Ze zijn de positieve reële getallen R+. Het bereik of de route zijn de reële cijfers R.

Ongeacht de basis gaat de logaritm -functie altijd door het punt (1.0) en het punt (a, 1) behoort tot de grafiek van deze functie.

Het kan u van dienst zijn: wachtrijtheorie: geschiedenis, model, waarvoor is het voor en voorbeelden voor

In het geval dat basis A groter is dan de eenheid (a> 1) neemt de logaritmefunctie toe. Maar ja (0 < a < 1) entonces es una función decreciente.

Seno, Coseno en raakwerkfuncties

De sinusfunctie kent een reëel getal en aan elke waarde x, waarbij x de maat voor een hoek in radianen vertegenwoordigt. Om de waarde van sen (x) vanuit een hoek te verkrijgen, wordt de hoek weergegeven in de eenheidscirkel en de projectie van deze hoek op de verticale as is de borst die overeenkomt met die hoek.

Hieronder is (in figuur 3) de trigonometrische cirkel en de borst voor verschillende hoekwaarden x1, x3, x3 en x4.

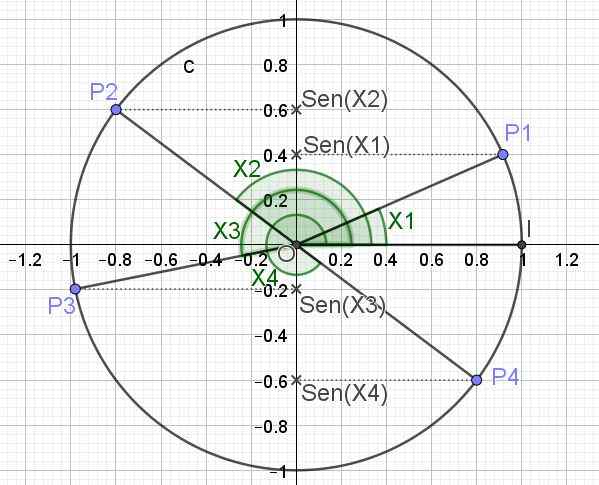figuur 3. Trigonometrische cirkel en de boezem van verschillende hoeken. (Eigen uitwerking)

Op deze manier gedefinieerd de maximale waarde die de Sen (x) -functie kan hebben, is 1, wat optreedt wanneer x = π/2 + 2π n, n een geheel getal is (0, ± 1, ± 2,). De minimale waarde die de Sen (x) -functie kan nemen wanneer x = 3π/2 + 2π n. 

De functie Coseno y = cos (x) is op een vergelijkbare manier gedefinieerd, maar de projectie van de hoekposities P1, P2, enz. Wordt uitgevoerd op de horizontale as van de trigonometrische cirkel.

Aan de andere kant is de functie y = tan (x) de verhouding tussen de sinusfunctie en de cosinusfunctie.

Vervolgens wordt een grafiek van de transcendente functies sen (x), cos (x) en tan (x) getoond

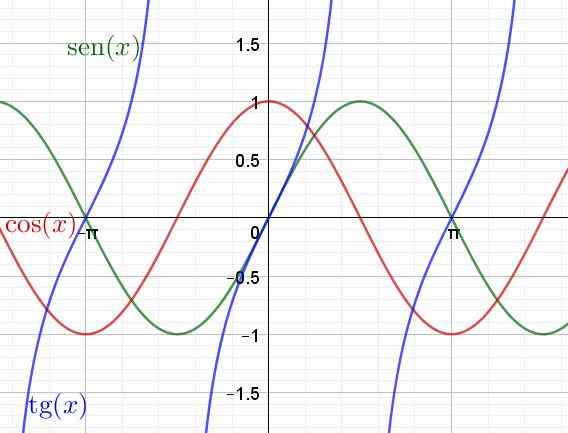Figuur 4. Grafiek van de transcendente functies, borst, cosinus en raaklijn. (Eigen uitwerking)

Afgeleid en integraal

Afgeleid van exponentiële functie

Het afgeleide En' van de exponentiële functie y = a^x Het is de functie a^x vermenigvuldigd door hem Neperian logaritm van de basis a:

Kan u van dienst zijn: theorie instellen: kenmerken, elementen, voorbeelden, oefeningen

en '= (a^x)' = a^x ln a

In het specifieke geval van de basis En, De afgeleide van de exponentiële functie is de exponentiële functie zelf.

Integraal van de exponentiële functie

De onbepaalde integraal van a^x Het is de functie verdeeld tussen de Neperiaanse logaritme van de basis. 

In het specifieke geval van basis E is de integrale van de exponentiële functie de exponentiële functie zelf.

Afgeleide en integrale tabel van de transcendente functies

Hieronder is een samenvattende tabel van de belangrijkste transcendente functies, de derivaten en onbepaald (antiderivaten):

Onbepaalde afgeleide en integrale tabel voor sommige transcendente functies. (Eigen uitwerking)

Voorbeelden

voorbeeld 1

Zoek de resulterende functie van de samenstelling van de functie f (x) = x^3 met de functie g (x) = cos (x):

(f of g) (x) = f (g (x)) = cos³(X)

Zijn afgeleide en zijn onbepaalde integrale is:

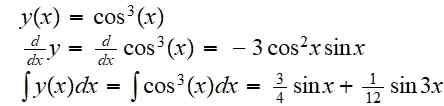
Voorbeeld 2

Zoek de samenstelling van de G -functie met de F -functie, zijnde g en F de functies die in het vorige voorbeeld zijn gedefinieerd:

(g of f) (x) = g (f (x)) = cos (x³))

Opgemerkt moet worden dat de samenstelling van functies geen commutatieve operatie is.

De afgeleide en de onbepaalde integrale voor deze functie zijn respectievelijk:

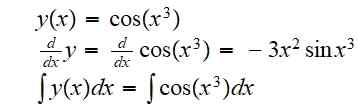
De integraal werd aangegeven omdat het niet mogelijk is om het resultaat op een exacte manier als een combinatie van elementaire functies te schrijven.

Referenties

1. Calculus van een enkele variabele. Ron Larson, Bruce H. Edwards. Cengage Learning, 10 november. 2008
2. De impliciete functie -stelling: geschiedenis, theorie en toepassingen. Steven G. Krantz, Harold R. Parken. Springer Science & Business Media, 9 november. 2012
3. Multivariabele analyse. Sable Shirali, Harkrishan Lal Vasudeva. Springer Science & Business Media, 13 december. 2010
4. Systeemdynamiek: modellering, simulatie en controle van mechatronische systemen. Dean C. Karnopp, Donald L. Margolis, Ronald C. Rosenberg. John Wiley & Sons, 7 maart. 2012
5. Calculus: wiskunde en modellering. William Bauldry, Joseph R. Fiedler, Frank R.Giordano, Ed Lodi, Rick Vitray. Addison Wesley Longman, 1 januari. 199999
6. Wikipedia. Transcendente functie. Hersteld van: is.Wikipedia.com