Exponentiële functie -eigenschappen, voorbeelden, oefeningen

De exponentiële functie Het is een wiskundige functie van groot belang voor de vele toepassingen die het heeft. Het wordt als volgt gedefinieerd:

f (x) = b^X, Met b> 0 en b ≠ 1

Waarbij B een echte constante altijd positief is en verschilt van 1, die bekend staat als baseren. Merk op dat de echte variabele X wordt gevonden in de exponent, Op deze manier is f (x) altijd een reëel getal.

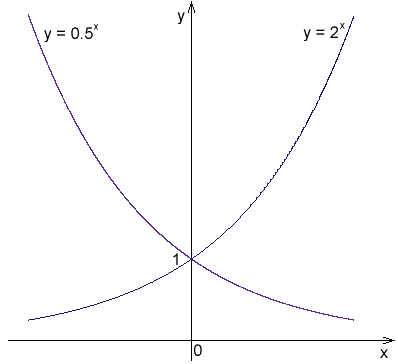Figuur 1. Exponentiële functies met basen 2 en 1/2

Voorbeelden van exponentiële functies zijn de volgende:

-f (x) = 2^X

-g (x) = 5⋅E^-3x

-H (x) = 4⋅ (10^2x))

Dit zijn functies die groeien - of afnemen, volgens het teken van de exponent - heel snel, dus er is sprake van de "exponentiële groei" wanneer een grootte zeer snel toeneemt. Daarom zijn ze gepast om de groei van levende wezens te modelleren, zoals bacteriën.

Een andere zeer interessante toepassing is die van samengestelde rente. Hoe meer geld je op een rekening hebt, hoe meer belangen, en ze kunnen elk bepaald tijdsinterval berekenen, zo klein als je wilt.

Met behulp van de logaritmische functie, die de omgekeerde functie van de exponentiële is, kan het bekend zijn na hoe lang een bepaald kapitaal toeneemt tot een bepaalde waarde.

[TOC]

Exponentiële functie -eigenschappen

Figuur 2. Voorbeelden van exponentiële functies. Bron: f. Zapata.

De volgende zijn de algemene eigenschappen van elke exponentiële functie:

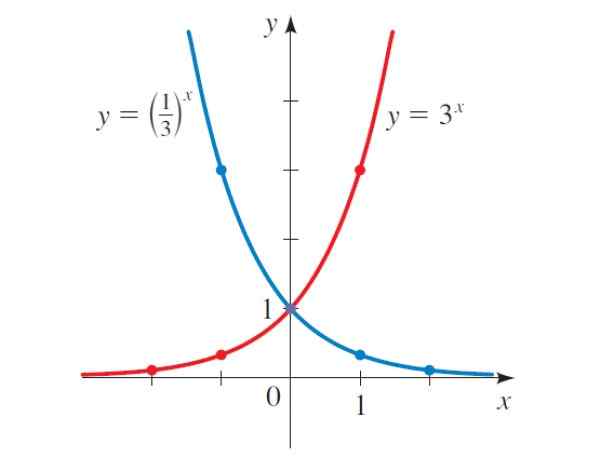
-De grafiek van elke exponentiële functie snijdt altijd de verticale as op het punt (0,1), zoals te zien is in figuur 2. Dit komt omdat B⁰ = 1 voor elke B -waarde.

-De exponentiële functie snijdt niet op de X -as, in feite is deze as een horizontale asymptoot voor de functie.

-Sinds B¹ = B, punt (1, b) hoort altijd bij de functieafbeeldingen.

Het kan je van dienst zijn: hepagonaal prisma

-Het domein van de exponentiële functie is de set van reële getallen en f (x) = b^X Het is continu in al zijn domein.

-Het bereik van exponentiële functie is allemaal reële getallen groter dan 0, wat ook wordt opgemerkt bij de afbeeldingen.

-De exponentiële functie is één voor één, dat wil zeggen dat elke X -waarde die tot het domein van de functie hoort, een uniek beeld heeft in de aankomstset.

-Het omgekeerde van de exponentiële is de logaritmische functie.

Bepaalde eigenschappen van exponentiële functie

Zoals we eerder hebben gezegd, kan de exponentiële functie toenemen of afnemen.

Als de grafiek van figuur 2 zorgvuldig wordt bestudeerd, wordt opgemerkt dat als b> 1, de functie groeit, bijvoorbeeld y = 3^X, Maar in het geval van y = (1/3)^X, met B < 1, la función decrece.

We hebben twee soorten exponentiële functies met de volgende specifieke eigenschappen:

Voor b> 1

-De functie groeit altijd.

-Wanneer de waarde van B toeneemt, groeit de functie sneller, bijvoorbeeld y = 10^X groeit sneller dan y = 2^X.

-Wanneer de variabele groter is dan 0, verwerft de functie waarden groter dan 1, dat wil zeggen:

Voor x> 0: y> 1

-En als x<0, entonces f(x) < 1.

Voor B < 1

-De functie neemt altijd af.

-Door de waarde van B te verlagen, neemt de functie nog steeds sneller af. Bijvoorbeeld y = (1/5)^X neemt sneller af dan y = (1/3)^X.

-Voor waarden van x lager dan 0, neemt de functie waarden groter dan 1, dat wil zeggen:

Voor x 1

-Eindelijk, wanneer x> 0, dan en < 1.

Voorbeelden van exponentiële functies

De exponentiële functie is zeer nuttig voor het modelleren van fenomenen in de wetenschap en de economie, zoals we hieronder zullen zien:

Natuurlijke exponentiële functie

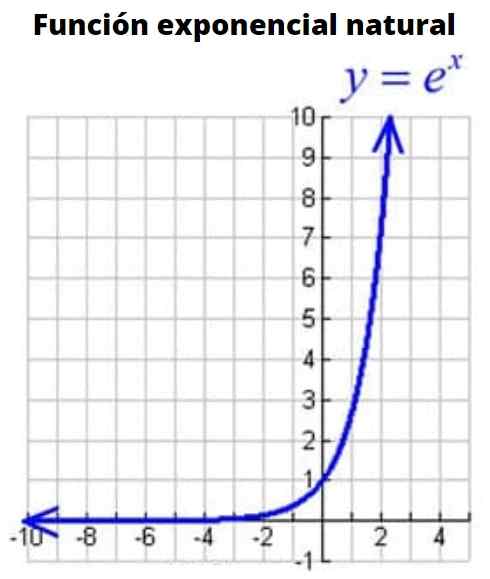Figuur 3: Natuurlijke exponentiële functiegrafiek

Het is de functie waarvan de basis het nummer E- of Euler -nummer is, een irrationeel nummer waarvan de waarde is:

Kan u van dienst zijn: aanvullende hoeken: wat zijn, berekening, voorbeelden, oefeningen

E = 2.718181828…

Deze basis werkt, zelfs als het geen ronde nummer is, heel goed voor tal van toepassingen. Daarom wordt het beschouwd als de belangrijkste basis van alle exponentiële functies. De natuurlijke exponentiële functie wordt op wiskundige manier uitgedrukt als:

f (x) = e^X

De exponentiële functie verschijnt vaak in waarschijnlijkheid en statistieken, omdat verschillende waarschijnlijkheidsverdelingen, zoals normale verdeling, Poisson en andere, kunnen worden uitgedrukt door exponentiële functies.

Continue samengestelde interesse

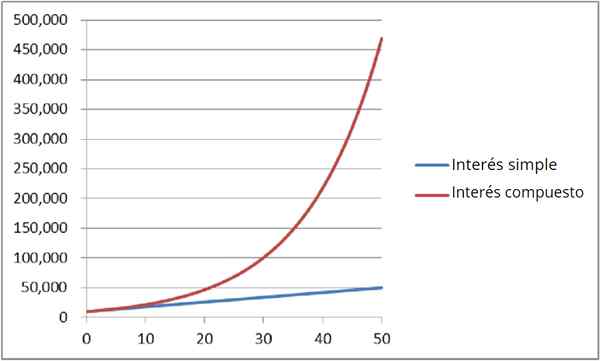Figuur 4: Vergelijking van eenvoudige en samengestelde interesse

Het wordt ook genoemd Continue kapitalisatie. Om de hoeveelheid geld te weten NAAR Je hebt na T Jaren wordt exponentiële uitdrukking gebruikt:

A (t) = p ⋅ e^RT

Waar P het bedrag is dat oorspronkelijk wordt gedeponeerd, is R de rente per jaar en ten slotte T is het aantal jaren.

Bacteriegroei

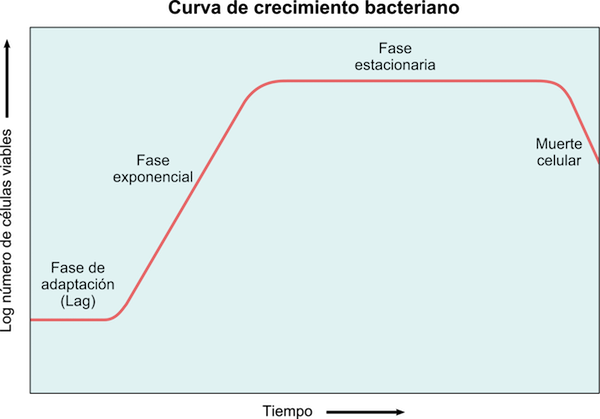Figuur 5: Bacteriële groeicurve waarbij de latentie, exponentiële, stationaire en dodenfasen worden waargenomen

Bacteriën groeien exponentieel, dus groei kan worden gemodelleerd door:

N (t) = n_of ⋅ e ^KT

Waarbij n (t) de bestaande bevolking is na tijd t (bijna altijd in uren), n_of Het is de initiële populatie en K is een constante die afhankelijk is van het bacterietype en de omstandigheden waaronder de beschikbare voedingsstoffen.

Radioactief verval

Bepaalde kernen in de natuur zijn onstabiel, dus weigeren ze te transformeren in stabielere, een proces dat heel kort kan zijn of duizenden jaren kan duren, afhankelijk van de isotoop. Tijdens de radioactieve verval worden deeltjes uitgestoten en soms ook fotonen.

Sommige radioactieve isotopen hebben medische toepassingen, bijvoorbeeld de radioactieve jodium I-131, die artsen gebruiken bij de diagnose en behandeling van bepaalde schildklieraandoeningen.

Radioactief verval wordt gemodelleerd door een exponentiële functie.

Kan u van dienst zijn: hoeveel tienden zijn er in een eenheid?

Opgeloste oefeningen

De vergelijkingen waarin het onbekende als exponent verschijnt, worden exponentiële vergelijkingen genoemd. Om de waarde van de onbekende te wissen, worden verschillende algebraïsche manipulaties gebruikt en het gebruik van de logaritm -functie, die de omgekeerde functie is van de exponentiële.

Laten we eens kijken naar enkele opgeloste oefeningen die het punt illustreren.

- Oefening 1

Los de volgende exponentiële vergelijkingen op:

tot 5^X = 625

B) 5^X = 2^X-1

Oplossing voor

Het nummer 625 is een veelvoud van 5, in feite, wanneer we het ontbinden, vinden we dat:

625 = 5⁴

Daarom kunnen we schrijven:

5^X = 5⁴

Omdat de bases gelijk zijn aan zowel links als rechts, kunnen we de exponenten matchen en verkrijgen:

x = 4

Oplossing B

Voor deze oefening kunnen we geen toevlucht nemen tot de eerder gebruikte techniek, omdat de bases niet hetzelfde zijn. Maar we kunnen logaritme toepassen aan beide zijden van gelijkheid, op deze manier:

5^X = 2^X-1

Log (5^X) = log (2^X-1))

Nu wordt de volgende eigenschap van de logaritmen toegepast:

Log M^N = n⋅log m

En overblijft:

x⋅log 5 = (x-1) ⋅log 2

x⋅ (log 5 - log 2) = -log 2

x = - log 2 ÷ (log 5 - log 2)

- Oefening 2

Geef aan welke functie elk van de hieronder getoonde grafieken overeenkomt, komt overeen:

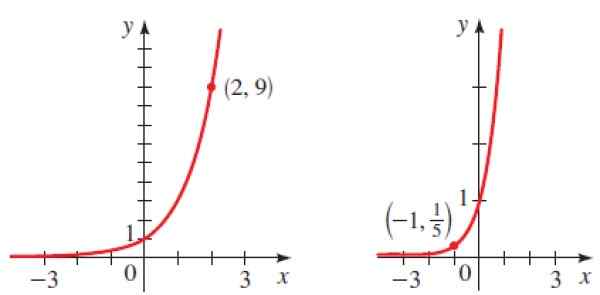Figuur 6. Grafische wijze parast de exponentiële functies van de opgeloste oefening 2. Bron: Stewart. J. Voorzetting.

Oplossing voor

Omdat het een groeiende grafiek is, is B groter dan 1 en we weten dat het punt (2.9) tot de grafiek behoort, daarom:

y = B^X → 9 = B²

We weten dat 3² = 9, daarom b = 3 en de functie is y = 3^X

Oplossing B

Weer vervangen we het gegeven punt (-1, 1/5) op y = b^X krijgen:

1/5 = B^-1 = 1/B

Dan B = 5 en de gezochte functie is:

y = 5^X

Referenties

1. Figuera, j. 20000000000000000000. Wiskunde 1e. Diversifieerd. Co-bo edities.
2. Gid Hoffmann, J. Selectie van wiskundeproblemen voor de 4e. Jaar. ED. SPPHINX.
3. Jiménez, r. 2008. Algebra. Prentice Hall.
4. Larson, r. 2010. Berekening van een variabele. 9NA. Editie. McGraw Hill.
5. Stewart, J. 2006. Precculment: wiskunde voor berekening. 5e. Editie. Cengage leren.