Elastische kracht wat bestaat, formules en oefeningen

De elastische kracht Het is de kracht die een object uitoefent om een ​​verandering in zijn vorm te weerstaan. Het manifesteert zich in een object dat de neiging heeft zijn vorm te herstellen wanneer het onder de werking van een vervormingskracht staat.

Elastische kracht wordt ook herstelkracht genoemd omdat het zich verzet tegen vervorming om objecten terug te brengen naar zijn evenwichtspositie. De overdracht van de elastische kracht is door de deeltjes die de objecten integreren.

Elastische sterkte van een veer

Wanneer bijvoorbeeld een metalen veer wordt gecomprimeerd, wordt een kracht die de veerdeeltjes duwt, uitgeoefend door de scheiding ertussen te verminderen, tegelijkertijd wordt de deeltjes geduwd die een kracht uitoefent die in strijd is met compressie.

Als het in plaats van de veer te comprimeren, wordt het uitrekken, de deeltjes die deze integreren, meer gescheiden. Evenzo verzetten de deeltjes zich weer aan het scheiden van een kracht die in strijd is met strekken.

Objecten die de eigenschap hebben om hun oorspronkelijke vorm te herstellen door de tegenstand te verzetten, worden elastische objecten genoemd. De veren, elastische rubber en elastische snaren zijn voorbeelden van elastische objecten.

[TOC]

Wat is de elastische kracht?

De elastische kracht (F_k) Het is de kracht die een object uitoefent om zijn staat van natuurlijk evenwicht te herstellen door te zijn beïnvloed door een externe kracht.

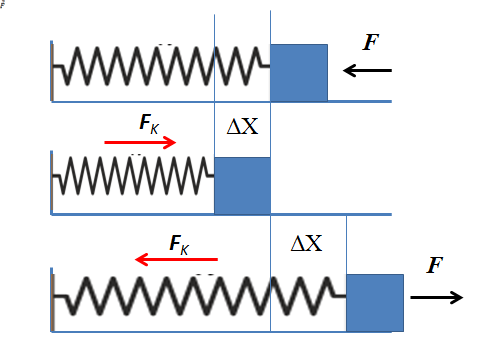
Om de elastische kracht te analyseren, zal rekening worden gehouden met het ideale veermassa -systeem dat bestaat uit een horizontaal geplaatste veer onderworpen aan het ene uiteinde aan de muur en aan de andere kant aan een blok van verachtelijke massa. De andere krachten die op het systeem werken, zoals wrijving of zwaartekracht zullen niet in aanmerking worden genomen.

Het kan u van dienst zijn: tweede evenwichtstoestand: uitleg, voorbeelden, oefeningen

Als een horizontale kracht op het deeg wordt uitgeoefend, gericht op de muur, wordt deze overgebracht naar de veer die deze comprimeert. De veer gaat van zijn evenwichtspositie naar een nieuwe positie. Aangezien het object de neiging heeft in evenwicht te blijven, manifesteert de elastische kracht zich in het voorjaar dat zich verzet tegen de uitgeoefende kracht.

De verplaatsing geeft aan hoeveel de veer en de elastische kracht is vervormd, is evenredig met die verplaatsing. Naarmate de veer wordt gecomprimeerd, neemt de variatie in de positie toe en verhoogt bijgevolg de elastische kracht.

Hoe meer de veer wordt gecomprimeerd, hoe meer oppositiekracht oefent totdat het een punt bereikt waar de uitgeoefende kracht en de elastische kracht in evenwicht zijn, bijgevolg het veermassasysteem stopt met bewegen. Door te stoppen met het toepassen van sterkte is de enige kracht die handelen de elastische kracht. Deze kracht versnelt de veer in de richting in strijd met de vervorming tot het herstellen van de staat van evenwicht.

Op dezelfde manier komt het voor bij het uitrekken van de veer naar het deeg horizontaal kijken. De veer is uitgerekt en oefent onmiddellijk een kracht uit die evenredig is aan verplaatsing tegen zich uitstrekken.

Formules

De elastische krachtformule wordt uitgedrukt door de wet van Hooke. Deze wet stelt vast dat de lineaire elastische kracht die door een object wordt uitgeoefend evenredig is met verplaatsing.

F_k = -k.ΔS         [1]

F_k = Elastische kracht

k = Evenredigheid constant

ΔS = Verplaatsing

Wanneer het object horizontaal beweegt, zoals in het geval van de veer onderworpen aan de muur, is de verplaatsing ΔX, En de uitdrukking van de wet van Hooke is geschreven:

F_k = -k.ΔX        [2]

Kan u van dienst zijn: convergente lens: kenmerken, typen en oefening opgelost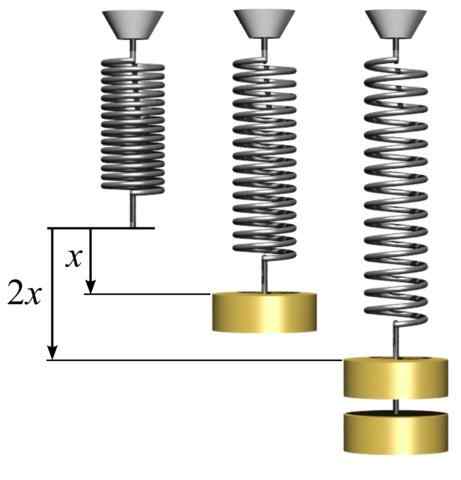Hooke's wet. Elastische kracht evenredig met het strekken. [Door svjo (https: // commons.Wikimedia.org/wiki/bestand: Hookes-Law-Springs.Png)]

Het negatieve teken in de vergelijking geeft aan dat de elastische kracht van de veer in de tegenovergestelde richting is van de kracht die de verplaatsing heeft veroorzaakt. De evenredigheid constant k Het is een constante die afhangt van het type materiaal waaraan de veer wordt gevormd. De eenheid van de constante k is N/m.

Elastische objecten hebben een elasticiteitslimiet die zal afhangen van de vervormingsconstante. Als het zich uitstrekt voorbij de elastische limiet, zal het permanent vervormen.

Vergelijking [1] en [2] is van toepassing op kleine verplaatsingen. Wanneer de verplaatsingen groter zijn, worden termen toegevoegd met een grotere kracht van ΔX.

Kinetische energie en potentiële energie verwezen naar een elastische kracht

De elastische kracht werkt in de lente door hem naar zijn evenwichtspositie te verplaatsen. Tijdens dat proces neemt de potentiële energie van het veermassasysteem toe. De potentiële energie als gevolg van het werk dat door de elastische kracht wordt uitgevoerd, wordt uitgedrukt in vergelijking [3].

U = ½ K .  Δx²[3]

Potentiële energie wordt uitgedrukt in Joules (J).

Door te stoppen met het toepassen van de vervormingskracht, versnelt de veer naar de evenwichtspositie door potentiële energie te verminderen en kinetische energie te vergroten.

De kinetische energie van het veermassa -systeem, wanneer de evenwichtspositie bereikt, wordt bepaald door vergelijking [4].

EN_k= ½ m.v²[4]

M = massa

v = Springsnelheid

Om het Spring Mass System op te lossen, wordt de tweede wet van Newton toegepast, rekening houdend met dat elastische kracht een variabele kracht is.

Praktische oefeningen van voorbeelden

Het verkrijgen van vervormingskracht

Hoeveel kracht is nodig om op een veer aan te brengen om 5 cm te rekken als de veerconstante 35n/m is?

Kan u van dienst zijn: versnelling van de zwaartekracht: wat is het, hoe het wordt gemeten en oefeningen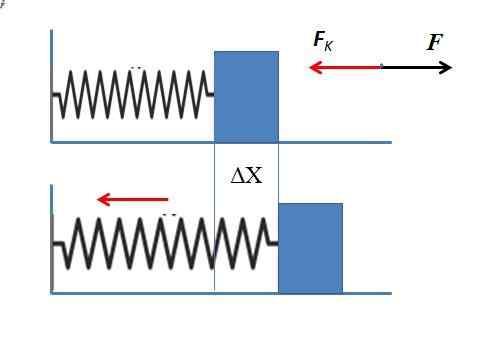Elastische kracht van een veer die 5 cm uitrekt

Naarmate de kracht van toepassing is tegen de elastische kracht wordt bepaald F_k Ervan uitgaande dat de veer horizontaal is uitgerekt. Het resultaat vereist niet het negatieve teken, omdat de toepassingskracht alleen nodig is.

Hooke's wet

F_k = -k.Δx       

De constante k van de lente is 35n/m.

Δx = 5 cm = 0,05 m

F_k = -35n/m . 0,05 m

F_k = - 1.75n = - f

Nodig zijn 1.75 n van kracht om de lente te vervormen 5 cm.

Het verkrijgen van de vervormingsconstante

Wat is de vervormingsconstante van een veer die zich uitstrekt 20 cm door de actie van een kracht van 60N?

Δx =20 cm = 0,2 m

F = 60N

F_k = -60n = - f

K = - f_k / Δx

  = -(-60n) /0.2m

K = 300 N/M

De veerconstante is 300n/m

Het verkrijgen van potentiële energie

Wat is de potentiële energie die wordt verwezen naar het werk dat wordt gedaan door de elastische kracht van een veer die wordt gecomprimeerd 10 cm En de vervormingsconstante is 20n/m?

ΔX =10 cm = 0,1 m

K = 20 N/M

F_k = -20n/m . 0,1 m

F_k = -200N

De elastische kracht van de veer is -200n.

Deze kracht werkt in de lente om hem naar zijn evenwichtspositie te verplaatsen. Bij het uitvoeren van dit werk neemt de potentiële energie van het systeem toe.

Potentiële energie wordt berekend met vergelijking [3]

U = ½ K .  Δx²

U = ½ (20n/m) . (0,1 m)²

U = 0,1joules

Referenties

1. Kittel, C, Knight, W D en Ruderman, M A. Mechanica. VS: Mc Graw Hill, 1973, Vol. Je.
2. Rama Reddy, K, Badami, S B en Balasubramanian, V. Oscillamenten en golven. India: University Press, 1994.
3. Murphy, J. Fysica: het ondernemen van de eigenschappen van materie en energie. New York: Britannica Educational Publishing, 2015.
4. Giordano, n J. College Fysica: redeneren en relaties. Canada: Brooks/Cole, 2009.
5. Walker, J, Halliday, D en Resnick, r. Fundamentals of Physics. VS: Wiley, 2014.