Viskeuze wrijving (kracht) coëfficiënt en voorbeelden

De viskeuze wrijving Het ontstaat wanneer een vast object in het midden van een vloeistof -un gas of een vloeistof beweegt-. Het kan worden gemodelleerd als een kracht die evenredig is aan het negatieve van de snelheid van het object of vierkant.

Het gebruik van een of ander model hangt af van bepaalde omstandigheden, zoals het type vloeistof waarin het object wordt verplaatst en of het al dan niet snel is. Het eerste model staat bekend als Lineaire weerstand, en daarin de omvang van viskeuze wrijving f_aanraken Het wordt gegeven door:

F_aanraken = ΓV

Figuur 1. Paracharidisten ervaren viskeuze kracht tijdens hun afdaling, omdat lucht weerstand biedt. Bron: Pixabay.

Hier is γ de constante van evenredigheid of coëfficiënt van viskeuze wrijving en V is de snelheid van het object. Het is van toepassing op lichamen die bij lage vloeistofsnelheden bewegen met een laminair regime.

In het tweede model, bekend als Kwadratische weerstand O Rayleight's wet, de omvang van de wrijvingskracht wordt berekend volgens:

F_aanraken = ½ ρ.NAAR.C_D.v²

Waarbij ρ de dichtheid van de vloeistof is, a is het kruissectionele gebied van het object en c_D Het is de aerodynamische weerstandscoëfficiënt.

Het product ½ ρ.NAAR.C_D  Het is een constante aerodynamica genaamd D, waarvan eenheden kg/m zijn, daarom:

F_aanraken = DV²

Dit model is geschikter wanneer de snelheid van objecten gemiddeld of hoog is, omdat de beweging turbulentie of wervelingen in zijn pad in de vloeistof produceert.

Een bewegende tennisbal en de auto's op de snelweg zijn voorbeelden van objecten waarin dit model vrij goed werkt.

De viscose -kracht ontstaat omdat de vaste stof de vloeistoflagen moet nemen om er doorheen te kunnen bewegen. Het bestaan ​​van verschillende modellen is omdat deze kracht afhankelijk is van meerdere factoren, zoals de viscositeit van de vloeistof, de snelheid en vorm van het object.

Kan u van dienst zijn: wat is relatieve permeabiliteit?

Er zijn meer aerodynamische objecten dan andere en velen zijn precies ontworpen, zodat de weerstand van het midden zijn snelheid tot een minimum vermindert.

[TOC]

Voorbeelden van viscose -wrijving

Elke persoon of object die in een vloeistof beweegt, ervaart noodzakelijkerwijs weerstand van de omgeving, maar vaak worden deze effecten veracht voor eenvoudige toepassingen zoals vrije val.

In de uitspraken van bijna alle problemen met de vrije val, wordt opgemerkt dat de effecten van luchtweerstand zichzelf verachten. Dit komt omdat lucht een nogal "dunne" vloeistof is en dat is waarom we hopen dat de wrijving die het niet significant biedt.

Maar er zijn andere bewegingen waarin viskeuze wrijving een meer beslissende invloed heeft, laten we enkele voorbeelden bekijken:

Stenen die in water en pollenkorrels vallen

-Een rots die verticaal in een buis vol olie valt, ervaart een kracht die zich verzet tegen zijn afdaling, dankzij vloeistofweerstand.

-De pollenkorrels zijn erg klein, dus voor hen is de weerstand van de lucht niet te verwaarlozen, want dankzij deze kracht slagen ze erin om lang te blijven drijven, waardoor seizoensgebonden allergieën worden veroorzaakt.

Figuur 2. Pollenkorrels zijn klein genoeg voor luchtweerstand om een ​​aanzienlijk effect te hebben. Bron: Pikrepo.

Zwemmers en fietsers

-In het geval van zwemmers gebruiken ze een hoed en scheren ze zich volledig zodat de weerstand van het water niet de snelheid aftrekt.

-Net als zwemmers ervaren fietsers in Counterreloj luchtweerstand, bijgevolg hebben helmen aerodynamische ontwerpen om de efficiëntie te verbeteren.

Ook is de competitie van de fietser binnen een groepsgroep relevant. Degene die de mars leidt, ontvangt kennelijk de grootste weerstand van de lucht, terwijl voor degenen die de mars sluiten, dit bijna nul is.

Het kan u van dienst zijn: tweede evenwichtstoestand: uitleg, voorbeelden, oefeningen

Paracharidisten

-Zodra een parachutist de parachute opent, wordt deze blootgesteld aan de viskeuze wrijving van de lucht, het meest geschikte model dat het kwadraat van de snelheid heeft. Op deze manier vermindert het zijn snelheid en omdat het wrijven tegen de val is, bereikt het een constante limietwaarde.

Auto

-Voor auto's is de aerodynamische weerstandscoëfficiënt, een constante die experimenteel wordt bepaald en het oppervlak dat het tegen de wind presenteert, de bepalende factoren om luchtweerstand te verminderen en het verbruik te verminderen. Daarom zijn ze ontworpen met hellende voorruiten.

Millikan's Oil Drop Experiment

-In het Millikan Oil Drop Experiment bestudeerde natuurkundige Robert Millikan de beweging van oliedruppels in het midden van een uniform elektrisch veld, waarmee hij concludeerde dat elke elektrische lading meervoud is van de elektronenbelasting.

Hiervoor was het noodzakelijk om de straal van de druppels te kennen, die niet door directe maatregel konden worden bepaald, gezien de kleine maat. Maar in dit geval was de viskeuze wrijving aanzienlijk en remmen de druppels uiteindelijk. Dit feit kon de straal van de druppels en vervolgens de elektrische lading bepalen.

Opdrachten

- Oefening 1

In de vergelijking voor viskeuze wrijvingskracht bij lage snelheid:

F_aanraken = ΓV

a) Welke dimensies moeten de viskeuze wrijvingscoëfficiënt γ hebben?

b) Wat zijn de γ -eenheden in het internationale systeem van eenheden?

Oplossing voor

In tegenstelling tot statische of kinetische wrijvingscoëfficiënten, heeft de viskeuze wrijvingscoëfficiënt afmetingen, wat moet zijn:

Kan u van dienst zijn: fysieke hechting: wat is en voorbeelden

Kracht / snelheid

De kracht heeft afmetingen van massa x lengte /tijd², terwijl snelheden lengte/tijd zijn. Door ze als volgt aan te geven:

-Massa: m

-Lengte: l

-Tijd: T

De afmetingen van de viskeuze wrijvingscoëfficiënt γ zijn:

[M.L /t²] / [L / t] = [m.L.T / l.T²] = M/t

Oplossing B

In de SI zijn de γ -eenheden kg/s

- Oefening 2

Rekening houdend met de weerstand waarover water zich verzet, is het vinden van een uitdrukking voor de terminale snelheid van een metalen sferiet die verticaal in een buis vol olie valt, in gevallen:

a) lage snelheid

b) Hoge snelheid

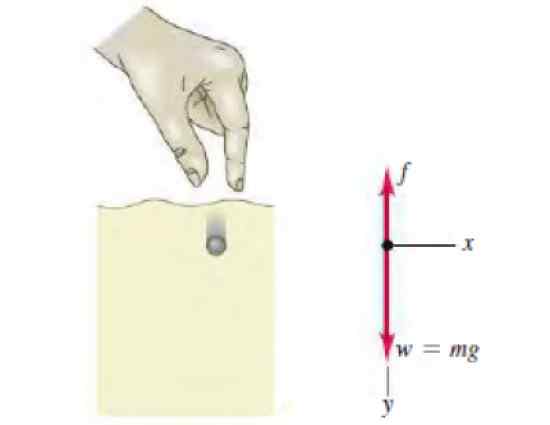figuur 3. Vrij lichaamsdiagram van een sferiet die binnen een vloeistof afdaalt. Bron: Sears, Z. Universitaire natuurkunde met moderne natuurkunde.

Oplossing voor

In de figuur verschijnt het vrije lichaamsdiagram en toont de twee krachten die op de sferiet werken: het gewicht naar beneden en de weerstand van de vloeistof, evenredig met de snelheid, omhoog. De tweede wet van Newton voor deze beweging stelt het volgende vast:

γV_T - Mg = 0

Waar v_T Het is de terminale snelheid, gegeven door:

v_T = mg / γ

Oplossing B

Als we het gemiddelde bij hoge snelheden veronderstellen, is het juiste model het model met vierkante snelheid:

F_aanraken = ½ ρ.NAAR.C_D.v²

Dus:

½ ρ.NAAR.C_D.v² - Mg = 0

D.v² - Mg = 0

v = √ [mg / d]

In beide situaties, hoe groter de massa van het object, hoe groter de terminale snelheid is.

Referenties

1. Serway, r., Jewett, J. (2008). Natuurkunde voor wetenschap en engineering. Deel 1. 7e. ED. Cengage leren.
2. Sears, Zemansky. 2016. Universitaire natuurkunde met moderne natuurkunde. 14e. ED. Deel 1.
3. Tipler, p. (2006) Natuurkunde voor wetenschap en technologie. 5e ed. Deel 1. Redactioneel teruggekeerd.
4. Tippens, p. 2011. Fysica: concepten en toepassingen. 7e editie. McGraw Hill
5. Sevilla University. Wrijvingskrachten. Hersteld van: laplace.ons.is.