Onstabiel balansconcept en voorbeelden

In mechanica is er een object in Onstabiele balans Wanneer het door het gewoon uit zijn positie met geweld te verplaatsen, komt het er niet naar terug. Bijvoorbeeld, de bal van de volgende figuur, wanneer deze boven de heuvel zich bevindt, bevindt zich in onstabiel evenwicht, omdat de minste verstoring op zijn kop zal komen, zonder de mogelijkheid om op zijn eigen middelen terug te keren.

Figuur 1. De bal bevindt zich in onstabiel evenwicht in de positie van links, in onverschillige balans in het midden en in stabiele balans rechts. Bron: Wikimedia Commons.

Aan de andere kant, wanneer de bal zich op een plat oppervlak bevindt, zoals in de positie van het midden, wordt gezegd dat deze zich bevindt onverschillig evenwicht of neutraal. Een kracht die het verstoort, kan worden uitgeoefend, het naar een andere kant verplaatsen, maar als de kracht verdwijnt, zal de bal weer stabiel zijn.

Eindelijk, aan de rechterkant, bevindt de bal zich op de bodem van een concave kom. Deze positie is ook evenwichtig, maar stabiel evenwicht. Een kracht die de bal verstoort, zal het alleen een beetje rond de oorspronkelijke positie laten oscilleren om er naar terug te keren.

[TOC]

Oorzaken van verlies van evenwicht

Gemeenschappelijke objecten (en mensen en dieren) verliezen hun evenwicht en vallen vanwege het koppel dat is ontstaan ​​door het gewicht, de kracht die door de aarde wordt uitgeoefend over alle objecten dicht bij het oppervlak. Wanneer u een uitgebreid lichaam hebt, wordt het punt waar het gewicht werkt zwaartekrachtcentrum.

Het gewicht kan worden gebalanceerd dankzij ondersteuning, zoals degene die een oppervlak biedt, en op deze manier zal het object niet bewegen. Maar heeft nog steeds de mogelijkheid om met betrekking tot een bepaald punt te draaien, omdat in uitgebreide objecten de krachtenbalans niet de enige factor is om ze stil te houden, maar ook de plaats waar deze krachten worden uitgeoefend.

Hieronder is er een figuur met een uitgebalanceerd potlood op de punt, in onstabiele balans. Elke luchtstroom zal het afzetten, maar ondertussen worden het normale gewicht en de kracht die zichzelf ondersteunt gecompenseerd. Bovendien hebben beide krachten dezelfde werklijn en dit gaat door het puntje van het potlood, waardoor de balans wordt gewaarborgd.

Kan u van dienst zijn: niet -Coplanar -vectoren: definitie, voorwaarden, oefeningen

Maar als het potlood slechts een beetje leunt, zoals aan de rechterkant wordt getoond, stopt de werklijn van het gewicht door de punt te passeren, die werkt als een draaipunt. Dan produceert het gewicht een niet -balanced koppel en draait het potlood in de richting van de klokken.

Figuur 2. Het potlood dat op zijn punt wordt ondersteund, bevindt zich in onstabiel evenwicht, een kleine verstoring zal ervoor zorgen dat het gewicht een koppel produceert ten opzichte van de punt en het potlood zal vallen. Bron: f. Zapata.

Factoren die stabiliteit garanderen

Bijna altijd wat wordt gezocht, is het stabiele evenwicht, omdat het onstabiele evenwicht, zoals de naam aangeeft, vrij precair is. Doorgaan met het voorbeeld van het potlood, zodra het valt en horizontaal op het oppervlak blijft, is de nieuwe positie veel stabieler dan toen deze op de punt werd gestopt.

Dit komt omdat enerzijds het zwaartepunt dichter bij het oppervlak is en anderzijds het steunoppervlak van het potlood is veel groter.

Wanneer het ondersteuningsoppervlak lar is. En als de afstand van het zwaartepunt tot het oppervlak lager is, is de arm van het gewichthendel lager en daarom is het koppel ook.

Concluderend, hoe groter de basis van ondersteuning van het object, en dichterbij zijn zwaartepunt naar de vloer dichterbij. Baby's weten het en daarom barsten ze meestal eerst voordat ze het risico lopen te staan.

En als het lichaam in plaats van wordt ondersteund, wordt het lichaam geschorst, heeft de locatie van het zwaartepunt ook een prominente rol bij het vaststellen van evenwicht, zoals binnenkort zal worden gezien in de volgende voorbeelden.

Kan u van dienst zijn: Mount Olympus (Mars)

Balansvoorbeelden

Evenwicht in ondersteunde lichamen

De balans in de ondersteunde lichamen hangt, zoals vermeld, af van:

-Hoe dicht het zwaartepunt van het oppervlak.

-De grootte van het objectbasis.

Overweeg een kegel op een platte tafel. De meest stabiele positie is zonder twijfel met de basis van de kegel die volledig op de tafel wordt ondersteund. Dit is de stabiele evenwichtspositie, omdat het zwaartepunt van de kegel zich op de as van symmetrie en dichter bij de basis bevindt dan bij de punt.

De onverschillige balans wordt bereikt door de leugen van de kegel te plaatsen en de onstabiele balans komt overeen met de kegel op zijn punt, zoals het potlood, wat misschien geen gemakkelijke taak is, gezien de kleinste beweging die de kegel draait.

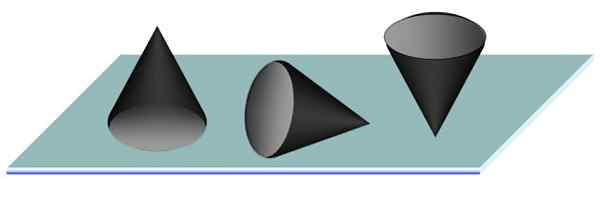figuur 3. Stabiele, onverschillige en onstabiele balans van een kegel die op een tafel wordt ondersteund. Bron: f. Zapata.

Evenwicht in opgehangen lichamen

Het is gebruikelijk om gesuspendeerde lichamen te vinden die ten minste één punt hangen, zoals schilderijen en lampen. Bij het vaststellen van het evenwicht is het noodzakelijk om de locatie van het zwaartepunt en die van het ophangpunt te overwegen.

De situatie is gemakkelijk te visualiseren met behulp van een rechthoekig kartonnen blad of een homogene materiaalregel. Hier valt het zwaartepunt samen met het geometrische centrum van de figuur, dat ervan uitgaande dat de massa van het object uniform is verdeeld.

Om het vel in onstabiel evenwicht te plaatsen, wordt het opgehangen aan een gevonden punt onder Vanuit het midden van de zwaartekracht houdt het zelfs het vel tussen de vingers vast zonder te veel aan te spannen, om hem te verplaatsing vrij te laten.

Een kleine kracht is voldoende om het vel in de een of andere zin onmiddellijk te roteren. De reden voor de beurt is hetzelfde als in het geval van het ondersteunde object: het gewicht oefent een compromis koppel uit dat de rotatie van het lichaam vergemakkelijkt.

Kan u van dienst zijn: oplossing Warmte: hoe het wordt berekend, toepassingen en oefeningen

Bij het draaien gaat het blad door een positie die van stabiel evenwicht is, waarin het suspensiepunt blijft van boven van het zwaartepunt. Rond deze positie varieert het een beetje en stopt uiteindelijk.

Als een kracht opnieuw wordt uitgeoefend, varieert de lamina opnieuw maar keert terug naar die positie, waarin het ophangpunt en het zwaartepunt zijn uitgelijnd met de verticale.

Ten slotte wordt de onverschillige balans gecontroleerd door een pin te passeren precies door het zwaartepunt. Als het blad wordt gedraaid om in verschillende posities te blijven, wordt gezien dat er geen groter verschil tussen hen zal zijn.

Concluderend, voor de lichamen die zijn opgehangen in onstabiel evenwicht, is het suspensiepunt onder het zwaartepunt. En het tegenovergestelde voor stabiele balans.

Referenties

1. Bauer, W. 2011. Fysica voor engineering en wetenschappen. Deel 1. MC Graw Hill.
2. Giancoli, D.  2006. Fysica: principes met toepassingen. 6e. Ed Prentice Hall.
3. Hewitt, Paul. 2012. Conceptuele fysieke wetenschap. 5e. ED. Pearson.
4. Resnick, r. (1999). Fysiek. Vol. 1. 3e ed. in het Spaans. Continental Editorial Company s.NAAR. van C.V.
5. Rex, a. 2011. Fundamentals of Physics. Pearson.
6. Sears, Zemansky. 2016. Universitaire natuurkunde met moderne natuurkunde. 14e. ED. Deel 1. Pearson.