Algemene vergelijking van een lijn waarvan de helling gelijk is aan 2/3

De algemene vergelijking van een lijn L is als volgt: Ax+door+C = 0, waarbij A, B en C constant zijn, X is de onafhankelijke variabele E en de afhankelijke variabele.

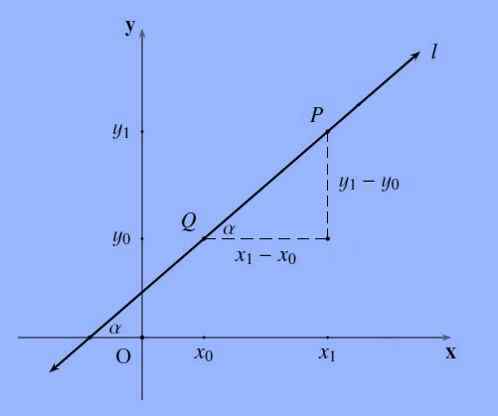
De helling van een lijn, op een algemene manier aangeduid door letter M, die de punten p = (x1, y1) en q = (x0, y0) doorgaat, is het volgende quotiënt m: = (y1-y0)/(x1 -X0).

De helling van een rechte lijn vertegenwoordigt de helling; Meer formeel gezegd, de helling van een lijn is de raaklijn van de hoek dat deze vorm met de X -as is.

Opgemerkt moet worden dat de volgorde waarin de punten worden genoemd onverschillig is, aangezien (y0-y1)/(x0-x1) =-(y1-y0)/(-(x1-x0)) = (y1-y0) /(X1-x0).

Hangende lijn

Als er twee punten bekend zijn waardoor een lijn voorbijgaat, is het gemakkelijk om zijn helling te berekenen. Maar wat gebeurt er als deze punten niet bekend zijn?

Gezien de algemene vergelijking van een bijl+door+c = 0 lijn, moet het.

Wat is de algemene vergelijking van een lijn waarvan de helling 2/3 is?

Omdat de helling van de lijn 2/3 is, wordt gelijkheid vastgesteld -a/b = 2/3, wat kan zien dat a = -2 en b = 3. Zodat de algemene vergelijking van een lijn met helling gelijk aan 2/3 -2x+3y+c = 0 is.

Het moet worden verduidelijkt dat als u wordt gekozen a = 2 en b = -3, dezelfde vergelijking wordt verkregen. Inderdaad, 2x -3y+C = 0, die gelijk is aan de vorige vermenigvuldigde met -1. Het teken van C doet er niet toe, omdat het een algemene constante is.

Een andere observatie die kan worden gemaakt, is dat voor a = -4 en b = 6 dezelfde lijn wordt verkregen, hoewel de algemene vergelijking ervan anders is. In dit geval is de algemene vergelijking -4x+6y+c = 0.

Zijn er andere manieren om de algemene vergelijking van de lijn te vinden?

Het antwoord is ja. Als de helling van een lijn bekend is, zijn er twee vormen, extra aan de vorige, om de algemene vergelijking te vinden.

Hiervoor worden de point-tending vergelijking en de snijvergelijking gebruikt.

-De point-a-vergelijking: als m de helling is van een lijn en p = (x0, y0) Een punt waar deze voorbijgaat, wordt de vergelijking y-y0 = m (x-x0) de point-pending vergelijking genoemd.

-De voorgesneden vergelijking: als m de helling van een lijn is en (0, b) is de snit van de lijn met de y-as, dan wordt de vergelijking y = mx+b de snijkantvergelijking genoemd.

Met behulp van het eerste geval wordt verkregen dat de punt-aansprekende vergelijking van een lijn waarvan de helling 2/3 is, wordt gegeven door de uitdrukking y-y0 = (2/3) (x-x0).

Om de algemene vergelijking te bereiken, worden alle termen vermenigvuldigd met 3 aan beide zijden en worden ze gegroepeerd, waardoor het verkrijgen van -2x+3y+(2 × 0-3y0) = 0 de algemene vergelijking van de lijn is, waarbij C = 2 × 0-3Y0.

Als het tweede geval wordt gebruikt, wordt verkregen dat de snij-voorhangende vergelijking van een lijn waarvan de helling 2/3 is, y = (2/3) x+b.

Nogmaals, het vermenigvuldigen van 3 aan beide zijden, en het groeperen van alle variabelen, het is verkregen -2x+3y -3b = 0. De laatste is de algemene vergelijking van de lijn waar C = -3B.

In beide gevallen is het in feite goed te bekijken dat het tweede geval gewoon een bepaald geval is van de eerste (wanneer x0 = 0).