90 divisors wat zijn en uitleg

De divisors van 90 zijn: 1, 2, 3, 5, 6, 9, 10, 15, 18, 30, 45 en 90.

Hoe wordt het berekend? We delen tussen de getallen die minder zijn dan 90 en wiens resultaat een geheel getal is:

• 90/1 = 90
• 90/2 = 45
• 90/3 = 30
• 90/5 = 18
• 90/6 = 15
• 90/9 = 10
• 90/10 = 9
• 90/15 = 6
• 90/18 = 5
• 90/30 = 3
• 90/45 = 2
• 90/90 = 1

Wat zijn de delers van 90?

De 90 divisors Ze zijn allemaal hele getallen zodanig dat door 90 onder hen te delen, het resultaat ook een geheel getal is. Dat wil zeggen, een volledig "A" -nummer is een deler van 90 als wanneer de 90 divisie wordt gemaakt tussen "a" (90 ÷ a), de rest van de genoemde divisie gelijk is aan 0.

Om te vinden wat de divisoren van 90 zijn, begint met het ontleden van 90 in prime factoren. Vervolgens worden alle mogelijke producten gemaakt tussen deze belangrijkste factoren. Alle resultaten zijn de 90 -.

De eerste delers die aan de lijst kunnen worden toegevoegd, zijn 1 en 90.

Wat zijn de delers uit de jaren 90?

Als alle divisors van het hierboven berekende nummer 90 zijn gegroepeerd boven de set 1, 2, 5, 6, 9, 15, 18, 30, 45.

Maar er moet aan worden herinnerd dat de definitie van de deler van een getal wordt toegepast op hele getallen, dat wil zeggen positief en negatief. Daarom is het aan de vorige set noodzakelijk om de negatieve gehele getallen toe te voegen die ook 90 verdelen.

De hierboven gemaakte berekeningen kunnen worden herhaald, maar het is te zien dat dezelfde getallen worden verkregen als voorheen, behalve dat alles negatief zal zijn.

Daarom zijn de lijst van alle delers van nummer 90:

± 1, ± 2, ± 3, ± 5, ± 6, ± 9, ± 15, ± 18, ± 30, ± 45, ± 90.

Uitleg

Een detail die zorg moet worden besteed, is dat, wanneer het over divisors van een geheel getal praat, impliciet wordt begrepen dat divisors ook hele getallen moeten zijn.

Dat wil zeggen, als het nummer 3 wordt overwogen, is te zien dat door 3 door 1 te delen.5, het resultaat is 2 (en de rest is gelijk aan 0). Maar 1.5 wordt niet beschouwd als een deler van 3 omdat deze definitie alleen voor hele getallen is.

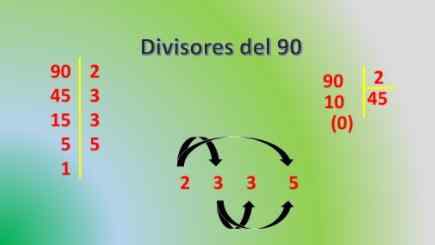
Bij het ontbinden van 90 in prime factoren kunt u zien dat 90 = 2*3²*5. Daarom kan worden geconcludeerd dat beide 2, 3 en 5 ook 90 divisors zijn.

We moeten alle mogelijke producten toevoegen tussen deze cijfers (2, 3, 5), rekening houdend met het feit dat 3 twee kracht hebben.

Mogelijke producten

Tot nu toe is de lijst met divisoren van nummer 90: 1,2,3,5,90. De andere producten die moeten worden toegevoegd, zijn de producten van slechts twee gehele getallen, drie gehele getallen en vier.

1.- Van twee gehele getallen:

Als het nummer 2 is ingesteld, neemt het product het formulier 2*_, de tweede plaats heeft slechts 2 mogelijke opties die 3 of 5 zijn, daarom zijn er 2 mogelijke producten die nummer 2 omvatten, namelijk: 2*3 = 6 en 2 *5 = 10.

Als het nummer 3 is ingesteld, blijft het product in het 3*_ -formulier, waarbij de tweede plaats 3 opties heeft (2, 3 of 5), maar de 2 niet kan worden gekozen, omdat het al in het vorige geval is gekozen. Daarom zijn er slechts 2 mogelijke producten die zijn: 3*3 = 9 en 3*5 = 15.

Als de 5 nu is opgelost, neemt het product het formulier 5*_ en de opties voor de tweede zijn 2 of 3, maar deze gevallen zijn al eerder overwogen.

Daarom zijn er in totaal 4 producten van twee gehele getallen, dat wil zeggen dat er 4 nieuwe delers van nummer 90 zijn: 6, 9, 10 en 15.

2.- Van drie gehele getallen:

Het begint door de 2 in de eerste factor in te stellen, waarna het product in de vorm 2*_*_ staat. De verschillende 3 factoren met het vaste nummer 2 zijn 2*3*3 = 18, 2*3*5 = 30.

Opgemerkt moet worden dat product 2*5*3 al is toegevoegd. Daarom zijn er slechts twee mogelijke producten.

Als de 3 wordt vastgesteld als de eerste factor, zijn de mogelijke producten van 3 factoren 3*2*3 = 18 (al toegevoegd) en 3*3*5 = 45. Daarom is er maar één nieuwe optie.

Concluderend zijn er drie nieuwe delers van 90 die zijn: 18, 30 en 45.

3.- Van vier gehele getallen:

Als het product van vier gehele getallen wordt overwogen, is de enige optie 2*3*3*5 = 90, die al vanaf het begin aan de lijst is toegevoegd.