Evenredigheid constant wat is, berekening, oefeningen

De evenredigheid constant Het is een relationeel numeriek element, dat wordt gebruikt om het gelijkenispatroon te definiëren tussen 2 magnitudes die tegelijkertijd zijn gewijzigd. Het is heel gebruikelijk om het weer te geven als een generieke lineaire functie door expressie f (x) = k.X. Dit is echter niet de enige weergave van een mogelijke evenredigheid.

De relatie tussen X en Y in de Y = 3x -functie heeft bijvoorbeeld een evenredigheidsconstante gelijk aan 3. Het laat zien dat wanneer de onafhankelijke variabele x groeit, de afhankelijke variabele ook en, in het drievoudige van de vorige waarde.

De wijzigingen die in de ene variabele worden toegepast, hebben onmiddellijke repercussies aan de andere kant, zodat er een waarde is die bekend staat als constant van evenredigheid. Dit dient om de verschillende grootten te relateren die beide variabelen verwerven.

[TOC]

Wat is de constante van evenredigheid en typen

Volgens de trend bij het wijzigen van de variabelen kunnen evenredigheid worden ingedeeld in 2 typen.

Directe evenredigheid

Suggereert een unidirectionele relatie tussen twee magnitudes. Daarin, als de onafhankelijke variabele enige groei presenteert, zal de afhankelijke variabele ook groeien. Evenzo zal elke afname van de onafhankelijke variabele een afname van de grootte van en.

De lineaire functie bijvoorbeeld die in de inleiding wordt gebruikt; Y = 3x, komt overeen met een directe verhouding van evenredigheid. Dit komt omdat de toename van de onafhankelijke variabele X een toename van drievoud zal veroorzaken in de vorige waarde die wordt genomen door de afhankelijke variabele en.

Evenzo zal de afhankelijke variabele zijn waarde drievoudig verlagen wanneer X in grootte afdaalt.

De waarde van de evenredigheidsconstante "k" in een directe relatie wordt gedefinieerd als k = y/x.

Omgekeerde of indirecte evenredigheid

In dit type functies wordt de relatie tussen de variabelen op een antoniem manier gepresenteerd, waarbij de groei of afname van de onafhankelijke variabele respectievelijk overeenkomt met de afname of groei van de afhankelijke variabele.

Het kan u van dienst zijn: ontleding van natuurlijke getallen (voorbeelden en oefeningen)

De functie f (x) = k/x is bijvoorbeeld een omgekeerde of indirecte relatie. Aangezien de waarde van de onafhankelijke variabele begint te stijgen, zal de waarde van K worden gedeeld door een groeiend figuur, waardoor de afhankelijke variabele in waarde afneemt volgens de verhouding.

Volgens de waarde van K kan de neiging van de proportionele omgekeerde functie worden gedefinieerd. Als k> 0, zal de functie in alle reële getallen afnemen. En de grafiek zal zich bevinden in het 1e en 3e kwadrant.

Integendeel, als de waarde van K negatief of kleiner is dan nul, zal de functie toenemen en zal de grafiek worden gevonden in het 2e en 4 kwadrant.

Hoe wordt het berekend?

Er zijn verschillende contexten waarin de definitie van de evenredigheidsconstante nodig kan zijn. In verschillende gevallen zullen verschillende gegevens over het probleem worden aangetoond, waarbij de studie hiervan eindelijk de waarde van k zal aantonen.

Op een generieke manier kan de bovengenoemde worden herhaald. De waarden van K komen overeen met twee uitdrukkingen volgens het aanwezige type evenredigheid:

- Direct: k = y/x

- Omgekeerd of indirect: k = y.X

Volgens uw grafiek

Soms zal alleen de grafiek van een functie gedeeltelijk of volledig bekend zijn. In deze gevallen zal dit nodig zijn, door grafische analyse, het type evenredigheid bepalen. Dan zullen we een coördinaat moeten definiëren waarmee de waarden van X en Y kunnen worden toegepast op de overeenkomstige K -formule.

De grafieken die verwijzen naar directe proportionaliteiten zijn van lineair type. Aan de andere kant krijgen de grafieken van omgekeerde proportionele functies meestal de vorm van hyperbolen.

Volgens de tabel met waarden

In sommige gevallen is er een tabel met waarden met de waarden die overeenkomen met elke iteratie van de onafhankelijke variabele. Normaal gesproken impliceert dit de realisatie van de grafiek naast het definiëren van de waarde van K.

Kan u van dienst zijn: frequentieverdeling: hoe u een tabel kunt maken, bijvoorbeeld, oefening

Volgens analytische expressie

Toont de uitdrukking die analytisch definieert. Direct de waarde van k kan duidelijk zijn, of deze kan ook worden afgeleid uit de uitdrukking zelf.

Als een regel van drie directe of samenstelling

In andere trainingsmodellen zijn er bepaalde gegevens, die verwijzen naar de relatie tussen waarden. Dit maakt de toepassing van drie directe of verbinding noodzakelijk om andere noodzakelijke gegevens in het jaar te definiëren.

Geschiedenis

Het concept van evenredigheid is altijd aanwezig geweest. Niet alleen in de geest en het werk van de grote wiskundigen, maar in het dagelijkse leven van de bevolking, vanwege hun bruikbaarheid en toepasbaarheid.

Het is heel gebruikelijk om te voldoen aan situaties die een evenredigheidsbenadering vereisen. Deze worden in elk geval gepresenteerd waar variabelen en fenomenen worden vergeleken die bepaalde relaties behouden.

Door een tijdlijn kunnen we historische momenten karakteriseren, waarin wiskundige vooruitgang met betrekking tot evenredigheid is toegepast.

- Tweede eeuw a.C. Het fractie- en verhoudingen opslagsysteem in Griekenland wordt aangenomen.

- 5e eeuw a.C. Het aandeel dat de zijkant en de diagonaal van een vierkant relateert, wordt ook ontdekt in Griekenland.

- 600 A.C. Tales de Mileto presenteert zijn stelling met betrekking tot evenredigheid.

- Jaar 900. Het decimale systeem dat eerder door India wordt gebruikt om redenen en verhoudingen wordt uitgebreid. Bijdrage van de Arabieren.

- Xvii eeuw. Bijdragen verwijzen naar de verhoudingen in de berekening van Euler die aankomen.

- XIX eeuw. Gauss biedt het concept van complex aantal en verhouding.

- Twintigste eeuw. Evenredigheid als functiemodel wordt gedefinieerd door suiker en deulofeo.

Opgeloste oefeningen

Oefening 1

Het is vereist om de waarde van de variabelen X, Y, Z en G te berekenen. De volgende proportionele relaties kennen:

3x + 2y - 6z + 8g = 1925

Kan u van dienst zijn: continue willekeurige variabele

x/3 = y/8 = z/3 = g/5

De relatieve waarden van de evenredigheidsconstante zijn gedefinieerd. Deze kunnen worden verkregen uit de tweede relatie, waarbij de waarde die elke variabele scheidt een relatie of reden met betrekking tot K aangeeft.

X = 3k y = 2k z = 3k g = 5k

Waarden worden vervangen in de eerste expressie, waarbij het nieuwe systeem wordt geëvalueerd in een enkele K -variabele.

3 (3K) + 2 (2k) - 6 (3k) + 8 (5k) = 1925

9k + 4k -18k + 40k = 1925

35k = 1925

K = 1925/35 = 55

Met behulp van deze waarde van de evenredigheidsconstante kunnen we de figuur vinden die elk van de variabelen definieert.

x = 3 (55) = 165 y = 2 (55) = 110

Z = 3 (55) = 165 g = 5 (55) = 275

Oefening 2

Bereken de evenredigheidsconstante en de uitdrukking die de functie definieert, gezien de afbeeldingen ervan.

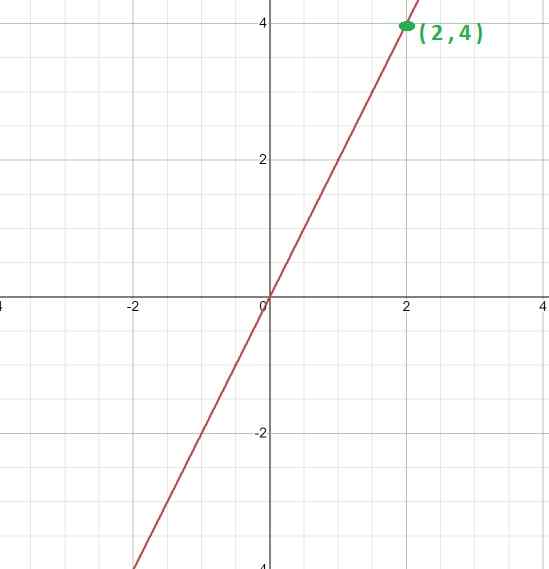
Ten eerste wordt de grafiek geanalyseerd, het lineaire karakter is duidelijk. Dit geeft aan dat het een functie is met directe evenredigheid en dat de waarde van K zal worden verkregen door de uitdrukking k = y/x

Vervolgens wordt een bepaalbaar punt van de grafiek gekozen, dat wil zeggen, een punt waarin de coördinaten die het samenstellen, precies kunnen zijn.

Voor deze zaak wordt het punt genomen (2, 4). Waar kunnen we de volgende relatie tot stand brengen.

K = 4/2 = 2

Zodat de uitdrukking wordt gedefinieerd door de Y = Kx -functie, die voor deze zaak zal zijn

F (x) = 2x

Referenties

1. Wiskunde voor elektriciteit en elektronica. Dr. Arthur Kramer. Cengage Learning, 27 juli. 2012
2. Vision 2020: De strategische rol van operationeel onderzoek. N. Ravichandran. Geallieerde uitgevers, 11 september. 2005
3. Grammaticale en rekenkundige kennis van de administratieve assistent van de staat.e-boek. Madduform
4. Wiskundeversterking voor curriculaire ondersteuning en diversificatie: voor curriculaire ondersteuning en diversificatie. Mª Lourdes Lázaro Soto. Narcea Ediciones, 29 augustus. 2003
5. Logistiek en commercieel management. Maria José Escudero Serrano. Paraninfo Editions, s.NAAR., 1 september. 2013