Integratie Constante betekenis, berekening en voorbeelden

De Integratieconstante Het is een extra waarde voor de berekening van de antiderivaten of integralen, het dient om de oplossingen weer te geven die de primitieve van een functie vormen. Drukt een inherente dubbelzinnigheid uit waarbij elke functie een oneindig aantal primitief heeft.

Bijvoorbeeld als de functie wordt genomen: f (x) = 2x + 1 en we krijgen het antiderivatief:

∫ (2x+1) dx = x² + X + C ; Waar C Het is de Integratieconstante en vertegenwoordigt grafisch de verticale vertaling tussen de oneindige mogelijkheden van primitief. Het is correct om dat te zeggen (x² + x) het is A van de primitieve f (x).

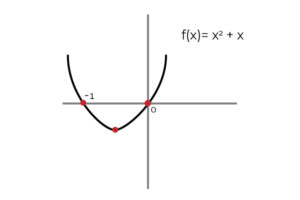Bron: auteur

Op dezelfde manier kunt u definiëren (x² + X + C ) als de primitieve van f (x).

[TOC]

Omgekeerde eigendom

Opgemerkt kan worden dat wanneer afgeleid de uitdrukking (x² + x) De functie f (x) = 2x + 1 wordt verkregen. Dit komt door de omgekeerde eigenschap tussen de afleiding en integratie van functies. Deze eigenschap maakt het mogelijk om integratie -formules te verkrijgen die vanaf differentiatie beginnen. Die de verificatie van integralen door dezelfde derivaten mogelijk maakt.

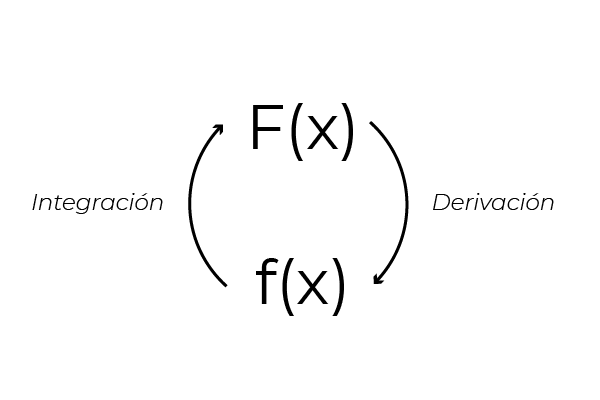Bron: auteur

Echter (x² + x) Het is niet de enige functie waarvan de afgeleide gelijk is aan (2x + 1).

1. D (X² + x)/ dx = 2x + 1
2. D (X² + x + 1)/ dx = 2x + 1 1
3. D (X² + x + 2)/ dx = 2x + 1 1
4. D (X² + x + 3)/ dx = 2x + 1 1
5. D (X² + X + C)/ dx = 2x + 1

Waarbij 1, 2, 3 en 4 een bijzondere primitieve van f (x) = 2x + 1 vertegenwoordigen. Terwijl 5 de onbepaalde of primitieve integrale van f (x) = 2x + 1 vertegenwoordigt.

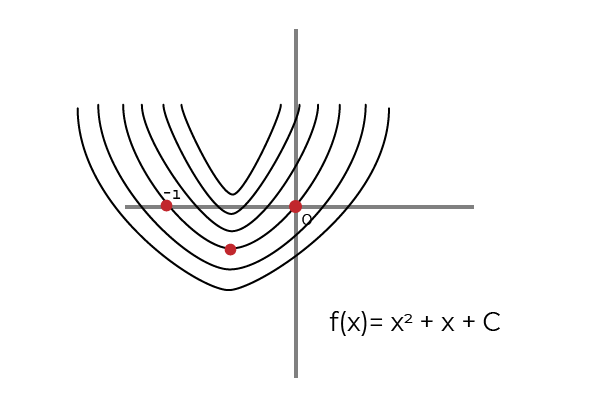Bron: auteur

De primitieve van een functie wordt bereikt door het antididivering of het integrale proces. Waar F een primitieve F zal zijn als het volgende is vervuld

• y = ∫ f (x) dx = F (x) + c; C = Integratieconstante
• F '(x) = f (x)

Het wordt op prijs gesteld dat een functie een enkele afgeleide heeft, in tegenstelling tot zijn oneindige primitieve als gevolg van integratie.

De onbepaalde integraal

 ∫ f (x) dx = f (x) + c

Het komt overeen met een familie van curven met hetzelfde patroon, die incongruentie ervaren in de waarde van de afbeeldingen van elk punt (x, y). Elke functie die dit patroon vervult, zal een individuele primitieve zijn en de set van alle functies staat bekend als Onbepaalde integraal.

De waarde van de Integratieconstante Het zal degene zijn die elke functie in de praktijk onderscheidt.

De Integratieconstante Het suggereert een verticale verplaatsing in alle grafieken die de primitieve van een functie vertegenwoordigen. Waar parallellisme tussen hen wordt waargenomen, en het feit dat C Het is de waarde van verplaatsing.

Volgens gemeenschappelijke praktijken Integratieconstante Het wordt aangeduid met de letter "C" na een toevoeging, hoewel het in de praktijk onverschillig is als de constante toevoegt of aftrekt. De werkelijke waarde ervan kan op verschillende manieren worden gevonden volgens verschillende begincondities.

Andere betekenissen van de integratieconstante

Er was al over hoe Integratieconstante wordt toegepast in de tak van integrale calculus; Een familie van curven vertegenwoordigen die de onbepaalde integrale definiëren. Maar veel andere wetenschappen en takken hebben zeer interessante en praktische waarden van de Integratieconstante, die de ontwikkeling van meerdere studies hebben vergemakkelijkt.

Kan u van dienst zijn: rechthoek trapezoid: eigenschappen, relaties en formules, voorbeelden

In de fysiek Integratieconstante kan meerdere waarden nemen op basis van de aard van de gegevens. Een veel voorkomend voorbeeld is om de functie te kennen V (t) die de snelheid van een deeltje versus de tijd t. Het is bekend dat bij het berekenen van een primitieve V (t) de functie wordt verkregen R (t) die de positie van het deeltje versus tijd.

De Integratieconstante zal de waarde van de beginpositie vertegenwoordigen, dat wil zeggen op het moment t = 0.

Evenzo, als de functie bekend is BIJ)  die de versnelling van het deeltje versus tijd. De primitieve van A (t) zal resulteren in functie v (t), waarbij de Integratieconstante Het zal de waarde zijn van de beginsnelheid v₀.

In de economie, Door de primitieve van een kostenfunctie te verkrijgen door integratie. De Integratieconstante zal de vaste kosten vertegenwoordigen. En zoveel andere toepassingen die differentiaal- en integrale calculus verdienen.

Hoe wordt de integratieconstante berekend?

Voor de berekening van de Integratieconstante, Het zal altijd nodig zijn om de begincondities. Die verantwoordelijk zijn voor het definiëren van welke van de mogelijke primitief de overeenkomstige is.

In veel toepassingen wordt het behandeld als een onafhankelijke variabele voor tijd (t), waar de constante C Neem de waarden die de begincondities van het specifieke geval.

Als het eerste voorbeeld is genomen: ∫ (2x+1) dx = x² + X + C

Een geldige initiële voorwaarde kan zijn om de afbeelding te conditioneren om door een specifieke coördinaat te gaan. Het is bijvoorbeeld bekend dat primitief (x² + X + C) Ga door het punt (1, 2)

F (x) = x² + X + C; Dit is de algemene oplossing

F (1) = 2

We vervangen de algemene oplossing in deze gelijkheid

F (1) = (1)² + (1) + C = 2

Waar het gemakkelijk wordt afgeleid C = 0

Op deze manier is de overeenkomstige primitieve voor deze zaak F (x) = x² + X

Er zijn verschillende soorten numerieke oefeningen die werken Integratieconstanten. In feite houdt differentiële en integrale calculus niet op om in het huidige onderzoek te worden toegepast. Op verschillende academische niveaus kun je vinden; Uit initiële berekening, door natuurkunde, chemie, biologie, economie, onder andere.

Het wordt ook gewaardeerd in de studie van differentiaalvergelijkingen, waar de Integratieconstante U kunt verschillende waarden en oplossingen nemen, dit vanwege de meerdere verwijzingen en integraties die in deze kwestie worden uitgevoerd.

Voorbeelden

voorbeeld 1

1. Een kanon op 30 meter hoge scheuten verticaal een projectiel op. Het is bekend dat de initiële projectielsnelheid 25 m/s is. Bepalen:

• De functie die de positie van het projectiel definieert ten opzichte van de tijd.
• De vluchttijd of tijdstijd waarin het deeltje de grond speelt.

Het kan u van dienst zijn: de 8 soorten meetfouten (met voorbeelden)

Het is bekend dat versnelling van een uniform gevarieerde rechtlijnige beweging een constante waarde is. Dit is het geval van de projectiellancering, waarbij versnelling de zwaartekracht zal zijn

G = - 10 m/s²

Het is ook bekend dat versnelling de tweede is afgeleid van de positie, die een dubbele integratie aangeeft in de resolutie van de oefening, waardoor er twee worden verkregen Integratieconstanten.

A (t) = -10

V (t) = ∫a (t) dt = ∫ (-10t) dt = -10t + C₁

De beginvoorwaarden van de oefening geven aan dat de initiële snelheid V is₀ = 25 m/s. Dit is de snelheid op het moment van tijd t = 0. Op deze manier is het vervuld dat:

V (0) = 25 = -10 (0) + C₁   En C₁ = 25

De snelheidsfunctie die wordt gedefinieerd

V (t) = -10t + 25; U kunt de gelijkenis zien met de MRUV -formule (V_F = V₀ + A x t)

In homoloog is de snelheidsfunctie geïntegreerd om de uitdrukking te bereiken die de positie definieert:

R (t) = ∫v (t) dt = ∫ (-10t+25) dt = -5t² + 25t + C₂

R (t) = -5t² + 25t + C₂  (Primitieve positie)

De initiële positie R (0) = 30 m is bekend. Dan wordt de specifieke primitieve van het projectiel berekend.

R (0) = 30m = -5 (0)² + 25 (0) + C₂ . Waar C₂ = 30

Sindsdien is het eerste gedeelte opgelost R (t) = -5t² + 25t + 30  ; Deze uitdrukking is homoloog voor de verplaatsingsformule in MRUV r (t) = r₀ + V₀T - GT²/2

Voor het tweede deel moet de kwadratische vergelijking worden opgelost: -5t² + 25t + 30 = 0

Aangezien het ervoor zorgt dat het deeltje de grond bereikt (positie = 0)

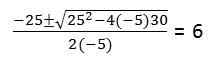Bron: auteur

Eigenlijk gooit de 2e klasse -vergelijking 2 oplossingen t: 6, -1. De waarde t = -1 wordt genegeerd omdat dit tijdseenheden zijn waarvan het domein geen negatieve getallen bevat.

Op deze manier is het tweede deel waar de vliegtijd gelijk is aan 6 seconden opgelost.

Voorbeeld 2

2. Zoek de primitieve f (x) die voldoet aan de beginvoorwaarden:

• f "(x) = 4; f '(2) = 2; f (0) = 7

Met de informatie van de tweede afgeleide f "(x) = 4 begint het antididiveringsproces

f '(x) = ∫f "(x) dx

∫4 dx = 4x + c₁

Vervolgens de voorwaarde f '(2) = 2 opbrengst:

4 (2) + C₁ = 2

C₁ = -6 en f '(x) = 4x - 8

Ga op dezelfde manier voor de tweede Integratieconstante

f (x) = ∫f '(x) dx
∫ (4x - 8) dx = 2x² - 8x + c₂

De initiële voorwaarde f (0) = 7 is bekend en gaat verder:

2 (0)² - 8 (0) + C₂ = 7

C₂ = 7 en f (x) = 2x² - 8x + 7

• f "(x) = x² ; f '(0) = 6; f (0) = 3

Net als het vorige probleem definiëren we de eerste derivaten en de oorspronkelijke functie van de beginvoorwaarden.

f '(x) = ∫f "(x) dx

∫ (x²) Dx = (x³/3) + c₁

Met voorwaarde f '(0) = 6 opbrengst:

Kan u van dienst zijn: theorie instellen: kenmerken, elementen, voorbeelden, oefeningen

(0³/3) + c₁ = 6; Waar₁ = 6 en f '(x) = (x³/3) + 6

Dan de tweede Integratieconstante

f (x) = ∫f '(x) dx

∫ [(x³/3) + 6] dx = (x⁴/12) + 6x + c₂

De initiële voorwaarde f (0) = 3 is bekend en gaat verder:

[(0)⁴/12] + 6 (0) + C₂ = 3; Waar₂ = 3

De specifieke primitieve wordt verkregen

f (x) = (X⁴/12) + 6x + 3

Voorbeeld 3

3. Definieer de primitieve functies gegeven de derivaten en een punt van de grafiek:

• dy/dx = 2x - 2 dat door het punt gaat (3, 2)

Het is belangrijk om te onthouden dat de derivaten verwijzen naar de helling van de lijn die op een bepaald punt naar de curve raakt. Waar het niet correct is om aan te nemen dat de afbeelding van de afgeleide het aangegeven punt raakt, omdat deze tot de grafiek van de primitieve functie behoort.

Op deze manier drukken we de differentiaalvergelijking als volgt uit:

dy = (2x - 2) DX  ; Bij het toepassen van de antididiveringscriteria heb je dan:

∫dy = ∫ (2x - 2) dx

y = x² - 2x + c

De initiële toestand toepassen:

2 = (3)² - 2 (3) + C

C = -1

Is verkregen: f (x) = x² - 2x - 1

• dy/dx = 3x² - 1 dat door het punt gaat (0, 2)

We drukken de differentiaalvergelijking als volgt uit:

dy = (3x² - 1) DX  ; Bij het toepassen van de antididiveringscriteria heb je dan:

 ∫dy = ∫ (3x² - 1) DX

y = x³ - x + c

De initiële toestand toepassen:

2 = (0)² - 2 (0) + C

C = 2

Is verkregen: f (x) = x³ - x + 2

Voorgestelde oefeningen

Oefening 1

1. Zoek de primitieve f (x) die voldoet aan de beginvoorwaarden:

• f "(x) = x; f '(3) = 1; f (2) = 5
• f "(x) = x + 1; f '(2) = 2; f (0) = 1
• f "(x) = 1; f '(2) = 3; f (1) = 10
• f "(x) = -x; f '(5) = 1; f (1) = -8

Oefening 2

2. Een ballon die stijgt met 16 voet/s snelheid brengt een zandjack vrij van een hoogte van 64 voet boven het maaiveld.

• Definieer vliegtijd
• Wat wordt de vector v_F Als je de vloer aanraakt?

Oefening 3

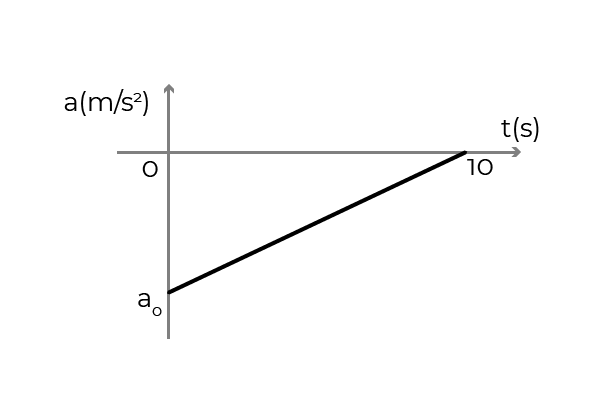
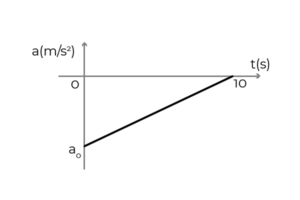
3. De figuur toont de versnellingsgrafiek - tijd van een auto die in de positieve zin van de X -as beweegt. De auto reed naar een constante snelheid van 54 km/u toen de bestuurder de remmen aanbracht om te stoppen in 10 seconden. Bepalen:

• De eerste versnelling van de auto
• De autosnelheid op t = 5s
• De verplaatsing van de auto tijdens het remmen

Bron: auteur

Oefening 4

4. Definieer de primitieve functies gegeven de derivaten en een punt van de grafiek:

• dy/dx = x dat door het punt gaat (-1, 4)
• dy/dx = -x² + 1 dat door het punt gaat (0, 0)
• dy/dx = -x + 1 die door het punt gaat (-2, 2)

Referenties

1. Integrale calculus. Onbepaalde integrale en integratiemethoden. Wilson, Velásquez Bastidas. Magdalena 2014 University
2. Stewart, J. (2001). Berekening van een variabele. Vroege transcendent. Mexico: Thomson Learning.
3. Jiménez, r. (2011). Wiskunde vi. Integrale calculus. Mexico: Pearson Education.
4. Natuurkunde I. MC Graw Hill