Conceptcoëfficiëntconcept, formule, berekening, voorbeeld

Hij Restitutiecoëfficiënt Het is het quotiënt tussen de relatieve snelheidssnelheid en de relatieve snelheid van het naderen van twee lichamen die botsen. Wanneer de lichamen na de botsing verenigd zijn, is dit quotiënt nietig. En de eenheid is de moeite waard in het geval dat de botsing perfect elastisch is.

Stel dat twee vaste massa -bollen M1 en massa M2 respectievelijk dat ze een botsing ondervinden. Vlak voor de botsing hadden de bollen snelheden V1 En V2 Met betrekking tot een bepaald traagheidsreferentiesysteem. Direct na botsing veranderen hun snelheden in V1 ' En V2 '.

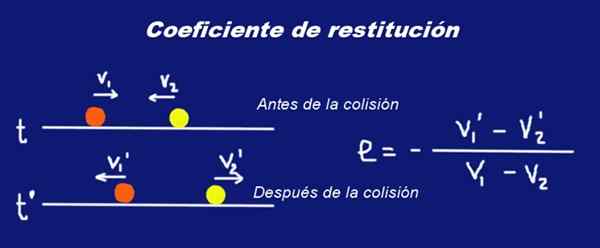Figuur 1. Botsing van twee massa's massa's M1 en M2 en hun restitutiecoëfficiënt en. Bereid door Ricardo Pérez.

Brief is geplaatst dikgedrukt lettertype In snelheden om aan te geven dat het vectorhoeveelheden zijn.

De experimenten geven aan dat elke botsing voldoet aan de volgende relatie:

V1 ' - V2 '= -En (V1 - V2)

Waar En Het is een reëel getal tussen 0 en 1, de genoemd Restitutiecoëfficiënt van de botsing. De vorige uitdrukking wordt als volgt geïnterpreteerd: 

De relatieve snelheid van twee deeltjes vóór de botsing is evenredig met de relatieve snelheid van de twee deeltjes na de botsing, de constante van evenredigheid is (-E), waarbij E de restitutiecoëfficiënt van de botsing is.

[TOC]

Waar is de restitutiecoëfficiënt voor?

Het nut van deze coëfficiënt ligt in het kennen van de mate van onelasticiteit van een botsing. In het geval dat de botsing volkomen elastisch is, zal de coëfficiënt 1 zijn, terwijl in een volledig inelastische botsing de coëfficiënt de waard zal zijn, omdat in dit geval de relatieve snelheid na de botsing nul is.

Wederzijds, als de restitutiecoëfficiënt van een botsing en de snelheden van de deeltjes er vóór bekend zijn, kunnen de snelheden worden voorspeld nadat een dergelijke botsing optreedt. 

Kan u van dienst zijn: 13 voorbeelden van de eerste wet van Newton in het echte leven

Het momentum

In botsingen, naast de relatie die is vastgesteld door de restitutiecoëfficiënt, is er een andere fundamentele relatie, Momentumbehoud.

Het momentum P van een deeltje, of hoeveelheid beweging zoals het ook wordt genoemd, het is het product van de massa M van het deeltje voor zijn snelheid V. Dat is: het momentum P Het is een vectorbedrag.

In botsingen het lineaire momentum P Het systeem is hetzelfde vlak voor en vlak na de botsing, omdat de buitenkracht verachtelijk is tegen de korte maar intense krachten van interne interactie tijdens de botsing. Maar het behoud van momentum is niet genoeg P van het systeem om het algemene probleem van de botsing op te lossen.

In het eerder genoemde geval, die van de twee M1- en M2 -bollen die botsen, is het behoud van het lineaire momentum als volgt geschreven:

 M1 V1 + M2 V2 = M1 V1 ' + M2 V2 ' .

Er is geen manier om het botsingsprobleem op te lossen als de restitutiekoëfficiënt niet bekend is. Momentumbehoud, hoewel noodzakelijk, is onvoldoende om snelheden na botsing te voorspellen.

Wanneer een probleem stelt dat de lichamen na de botsing samen bewegen, zegt impliciet dat de restitutiecoëfficiënt 0 is.

Figuur 2. In de biljartballen zijn er botsingen van restitutiecoëfficiënt iets minder dan 1. Bron: Pixabay.

Energie- en restitutiecoëfficiënt 

De andere belangrijke fysieke hoeveelheid die bij botsingen betrokken is, is energie. Tijdens botsingen zijn er beurzen van kinetische energie, potentiële energie en andere soorten energie, zoals calorie -energie.

Voor en na botsing is de potentiële energie -interactie praktisch nul, dus de energiebalans omvat de kinetische energie van de deeltjes voor en na en een hoeveelheid Q Dissipated Energy genoemd.

Het kan u van dienst zijn: Heisenberg Atomic Model

Voor de twee M1- en M2 -massa -bollen die de energiebalans voor en na de botsing botsen, is deze als volgt geschreven:

½ m1 V1^2 + ½ m2 V2^2 = ½ m1 V1 '^2 + ½ m2 V2 '^2 + Q

Wanneer de interactiekrachten tijdens de botsing puur conservatief zijn, gebeurt het dat Totale kinetische energie Van de deeltjes die het botsen is bewaard, dat wil zeggen, het is hetzelfde voor en na de botsing (q = 0). Wanneer dit gebeurt, wordt gezegd dat botsing volkomen elastisch is.

In gevallen van elastische botsingen wordt energie niet verdwenen. En ook de restitutiecoëfficiënt voldoet aan: E = 1. 

Integendeel, in inelastische botsingen die ≠ 0 en 0 ≤ e < 1. Sabemos, por ejemplo, que la colisión de las bolas de billar no es perfectamente elástica porque el sonido que se emite durante el impacto es parte de la energía disipada.

Om een ​​botsingsprobleem perfect te bepalen, is het noodzakelijk om de restitutiecoëfficiënt te kennen, of afwisselend de hoeveelheid energie die tijdens de botsing is verdwenen.

De restitutiecoëfficiënt is afhankelijk van de aard en het type interactie tussen de twee lichamen tijdens de botsing.

Aan de andere kant zal de relatieve snelheid van de lichamen vóór de botsing de intensiteit van de interactie en dus de invloed ervan op de restitutiecoëfficiënt bepalen. 

Hoe wordt de restitutiecoëfficiënt berekend?

Om te illustreren hoe de restitutiecoëfficiënt van een botsing wordt berekend, zullen we een eenvoudig geval nemen:

Stel dat de botsing van twee massaal bollen M1 = 1 kg En M2 = 2 kg Die beweging op een rechte wrijving (zoals in figuur 1).

De eerste sfeer beïnvloedt de initiële snelheid V1 = 1 m/s Ongeveer de tweede die oorspronkelijk in rust is, dat wil zeggen V2 = 0 m/s.

Het kan u van dienst zijn: eerste wet van thermodynamica: formules, vergelijkingen, voorbeelden

Na de botsing bewegen ze zo: de eerste stopt (V1 '= 0 m/s) en de tweede beweegt naar rechts met snelheid V2 '= 1/2 m/s.

Om de restitutiecoëfficiënt in deze botsing te berekenen, passen we de relatie toe:

V1 ' - V2 ' = -En (( V1 - V2 )) 

0 m/s - 1/2 m/s = - E (1 m/s - 0 m/s) => - 1/2 = - e => e = 1/2 .

Voorbeeld

In de ene -dimensionale botsing van de twee bollen van de vorige sectie werd de restitutiecoëfficiënt berekend, wat resulteerde in E = ½ .

Als e ≠ 1 is de botsing niet elastisch, dat wil zeggen, de kinetische energie van het systeem wordt niet bewaard en er is een hoeveelheid gedissipeerde energie Q (bijvoorbeeld verwarming van de bollen vanwege de botsing).

Bepaal de waarde van de energie die is verdwenen in joules. Bereken ook het percentage fractie van gedissipeerde energie.

Oplossing

De initiële kinetische energie van bol 1 is: 

K1i = ½ m1 v1^2 = ½ 1 kg (1 m/s)^2 = ½ j

Terwijl die van Sphere 2 nul is omdat hij aanvankelijk in rust is.

Dus de initiële kinetische energie van het systeem is ki = ½ j.

Na de botsing beweegt alleen de tweede bol met snelheid V2 '= ½ m/s, dus de uiteindelijke kinetische energie van het systeem zal zijn:

Kf = ½ m2 v2 '^2 = ½ 2 kg (½ m/s)^2 = ¼ j

Dat wil zeggen, de energie die in de botsing is verdwenen, is:

Q = ki - kf = (½ j - ¼ j) = 1/4 j

En de fractie van energie die in deze botsing is verdwenen, wordt als volgt berekend:

F = q / ki = ¼ / ½ = 0,5 dat wil zeggen dat 50% van de systeemergie is afgevoerd vanwege de inelastische botsing waarvan de restitutiecoëfficiënt 0,5 is.

Referenties

1. Bauer, W. 2011. Fysica voor engineering en wetenschappen. Deel 1. MC Graw Hill.
2. Figueroa, D. 2005. Serie: Physics for Science and Engineering. Deel 1. Kinematica. Uitgegeven door Douglas Figueroa (USB).
3. Ridder, r. 2017. Fysica voor wetenschappers en engineering: een strategiebenadering. Pearson.
4. Sears, Zemansky. 2016. Universitaire natuurkunde met moderne natuurkunde. 14e. ED. Deel 1.
5. Wikipedia. Hoeveelheid beweging.Hersteld van: is.Wikipedia.borg.