Hoe u de hoek van een driehoek kunt krijgen? (Voorbeeld)

Er zijn verschillende manieren van Bereken de zijkanten en hoeken van een driehoek. Deze zijn afhankelijk van het type driehoek waarmee u werkt.

Bij deze gelegenheid zal worden aangetoond hoe de zijkanten en hoeken van een rechter driehoek te berekenen, ervan uitgaande dat bepaalde driehoeksgegevens met kennissen met kennissen.

De elementen die zullen worden gebruikt, zijn:

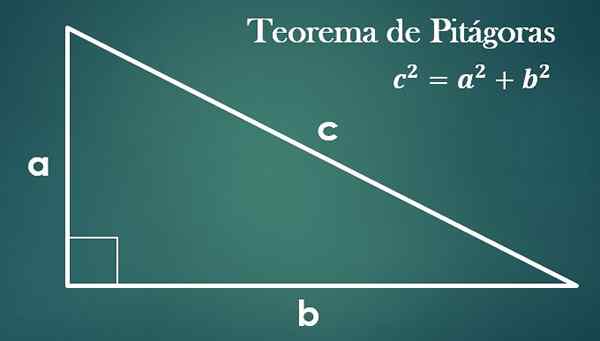
- de stelling van Pythagoras

Gegeven een rechthoekige driehoek met "a", "b" en hypotenusa "c", is het waar dat "c² = a²+b²".

- Gebied van een driehoek

De formule voor het berekenen van het gebied van een driehoek is a = (b × h)/2, waarbij "b" de lengte van de basis is en "h" de lengte van de hoogte.

- Hoeken van een driehoek

De som van de drie interne hoeken van een driehoek is 180 °.

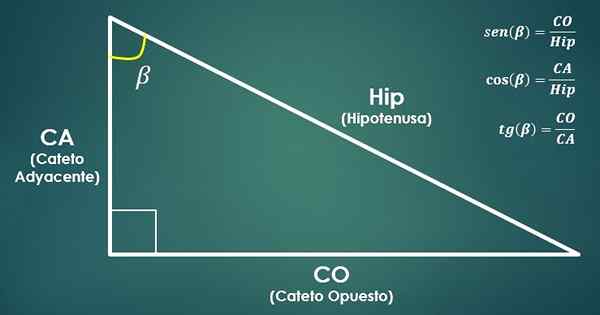
- Trigonometrische functies:

Overweeg een juiste driehoek. Vervolgens zijn de trigonometrische functies als volgt gedefinieerd sinus, cosinus en raaklijn van de bèta -hoek (β):

sin (β) = co/hyp, cos (β) = ca/heup en tan (β) = co/ca.

Hoe de zijkanten en hoeken van een rechter driehoek te berekenen?

Gegeven een ABC -rechthoekige driehoek, kunnen de volgende situaties worden gepresenteerd:

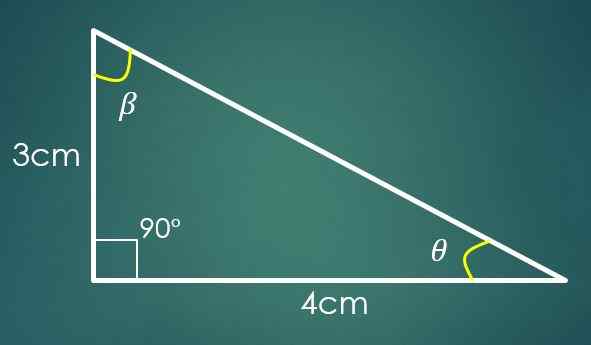
1- De twee benen zijn bekend

Als de cateto "a" 3 cm en de cateto "b" meet 4 cm, dan wordt de waarde van "c" de pythagoras -stelling gebruikt om te berekenen. Door de waarden van "A" en "B" te vervangen, wordt het verkregen dat C² = 25 cm², wat inhoudt dat C = 5 cm.

Als de hoek β nu tegengesteld is aan de categorie "B", dan is Sin (β) = 4/5. Bij het toepassen van de omgekeerde functie van de borst wordt in deze laatste gelijkheid verkregen dat β = 53,13º. Twee interne hoeken van de driehoek zijn al bekend.

Laat θ de hoek zijn die nog moet worden bekend, dan 90º+53.13º+θ = 180 °, waar het wordt verkregen dat θ = 36,87º.

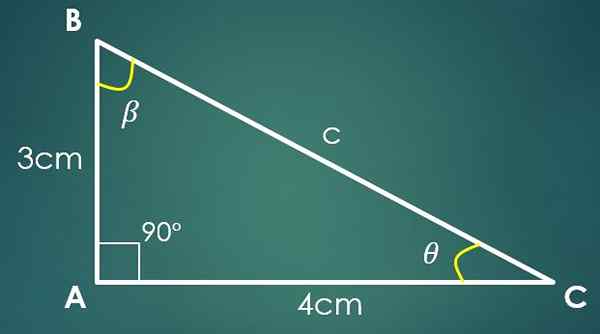
In dit geval is het niet nodig dat de bekende partijen de twee benen zijn, het belangrijkste is om de waarde van twee kanten te kennen.

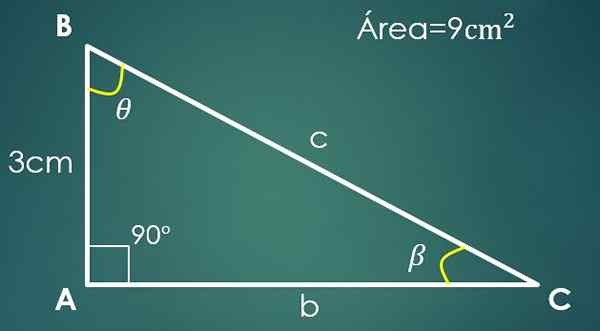
2- Een been en het gebied is bekend

Laat a = 3 cm het bekende been en 9 cm² het driehoekgebied.

In een rechthoekige driehoek kan een categorie als basis worden beschouwd en de andere als hoogte (omdat ze loodrecht zijn).

Stel dat "a" de basis is, daarom, 9 = (3 × h)/2, waar wordt verkregen dat de andere categorie 6 cm meet. Om de hypotenuse te berekenen, ga je verder zoals in het vorige geval en wordt verkregen dat c = √45 cm.

Als de hoek β nu tegengesteld is aan de "a" cateto, dan sin (β) = 3/√45. Bij het opruimen van β wordt verkregen dat de waarde ervan 26,57º is. U hoeft alleen de waarde van de derde hoek te weten θ.

Er wordt vervuld dat 90 °+26,57º+θ = 180 °, waar wordt geconcludeerd dat θ = 63,43º.

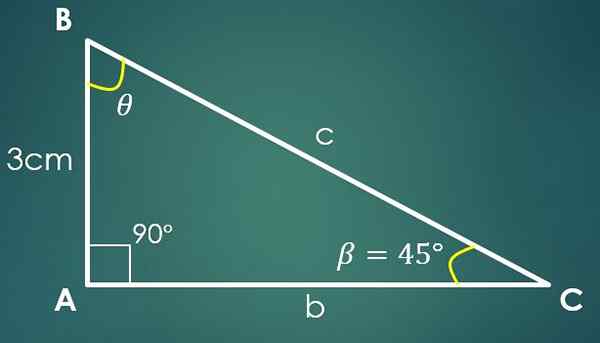
3- Een hoek en een cateto is bekend

Laat β = 45 ° de bekende hoek en a = 3 cm het bekende been, waarbij de cateto "a" tegen de hoek β is. Met behulp van de tangensformule wordt verkregen dat Tg (45 °) = 3/CA, waar het uitkomt dat Ca = 3 cm.

Met behulp van de Pythagoras -stelling wordt verkregen dat C² = 18 cm², dat wil zeggen C = 3√2 cm.

Het is bekend dat een hoek 90 ° meet en dat β 45 ° meet, vanaf hier wordt geconcludeerd dat de derde hoek 45 ° meet.

In dit geval hoeft de bekende zijde geen been te zijn, het kan een van de drie zijden van de driehoek zijn.