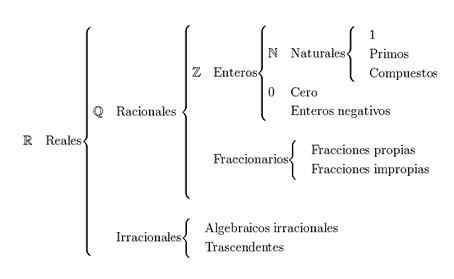
Classificatie van reële getallen

De belangrijkste Classificatie van reële getallen Het is verdeeld in natuurlijke getallen, hele getallen, rationele getallen en irrationele getallen. De reële getallen worden weergegeven met de letter r.

Echte getallen verwijzen naar de combinatie van rationele en irrationele getallengroepen. Om deze groepen te vormen, zijn er natuurlijke getallen en hele getallen nodig.

Er zijn veel manieren waarop de verschillende reële getallen kunnen worden gebouwd of beschreven, variërend van eenvoudiger vormen tot complexere vormen, afhankelijk van het wiskundige werk dat u wilt uitvoeren.

Hoe worden reële getallen geclassificeerd?

- Natuurlijke cijfers

Natuurlijke getallen worden weergegeven door letter (n) en zijn die worden gebruikt om te tellen (0,1,2,3,4 ...). Bijvoorbeeld "er is vijftien Rosas in de tuin "," De bevolking van Mexico is van 126 miljoenen van mensen "of" de som van twee En twee is vier". Opgemerkt moet worden dat sommige classificaties 0 omvatten als een natuurlijk nummer en andere niet. 

Twee kinderen die een som van twee natuurlijke getallen maken.

Natuurlijke cijfers omvatten niet die met een decimaal deel. Daarom is de bevolking van Mexico van 126.2 miljoenen mensen "of" maakt een temperatuur van 24.5 Celsius graden "Natuurlijke getallen konden niet worden overwogen.

In gemeenschappelijke taal, zoals basisscholen, kunnen natuurlijke getallen boekhoudnummers worden genoemd om negatieve gehele getallen en nul uit te sluiten.

Natuurlijke nummers zijn de bases waarmee vele andere sets van getallen kunnen worden gebouwd door uitbreiding: hele getallen, rationele getallen, reële getallen en complexe getallen, onder andere.

De eigenschappen van natuurlijke getallen, zoals de deelbaarheid en verdeling van primaire getallen, worden bestudeerd in de theorie. De problemen met het tellen en bestellen, zoals opsommingen en partitie, worden bestudeerd in de combinatorische.

Ze hebben verschillende eigenschappen, zoals: som, vermenigvuldiging, aftrekking, verdeling, enz.

Kan je dienen: hedendaagse wetenschap

Ordinale en kardinale nummers

Natuurlijke getallen kunnen ordinaal of kardinaal zijn.

Kardinale getallen zouden die zijn die worden gebruikt als natuurlijke getallen, zoals hierboven vermeld in de voorbeelden. "Hebben twee koekjes "," ik ben de vader van drie kinderen "," De doos omvat twee cadeaucrèmes ". 

Ordinals zijn die die de orde uiten of een positie aangeven. Bijvoorbeeld, in een race wordt de volgorde van aankomst van de lopers vermeld door de winnaar en het beëindigen van de laatste die naar de finish kwam.

Op deze manier zal worden gezegd dat de winnaar de "eerste" is, de volgende "tweede", de volgende "derde" enzovoort tot de laatste. Deze nummers kunnen worden weergegeven door een brief in hun rechtsboven om het schrijven te vereenvoudigen (1e, 2e, 3e, 4e, enz.)).

- Gehele getallen

De volledige getallen bestaan ​​uit die natuurlijke getallen en hun tegenstellingen, dat wil zeggen de negatieve getallen (0, 1, -1, 2, -2, 50, -50 ...). Net als natuurlijke cijfers omvatten deze niet degenen die een decimaal deel hebben.

Voorbeeld van hele getallen zou "gemiddeld 30e in Duitsland" zijn, "ik bleef om 0 na het bereiken van het einde van de maand", "om naar de kelder te gaan, moet je de liftknop" van de lift "markeren".

Op hun beurt kunnen hele getallen niet worden geschreven met een fractionele component. Bijvoorbeeld, nummers zoals 8.58 of √2 zijn geen hele getallen.

Hele getallen worden weergegeven met de letter (z). Z is een submail -groep van rationele nummers Q, die op zijn beurt de groep reële nummers vormen. Net als natuurlijke getallen is Z een oneindige boekhoudgroep.

Gehele getallen vormen de kleinste groep en de kleinste reeks natuurlijke nummers. In de theorie van algebraïsche getallen worden hele getallen soms irrationeel genoemd om ze te onderscheiden van algebraïsche gehele getallen.

Het kan u van dienst zijn: onderzoeksproject: partijen, hoe het is uitgewerkt en voorbeeld

- Rationele nummers

De set rationele getallen wordt weergegeven door letter (Q) en bevat al die getallen die kunnen worden geschreven als een fractie van hele getallen.

Dat wil zeggen, deze set omvat natuurlijke getallen (4/1), hele getallen (-4/1) en exacte decimale nummers (15,50 = 1550/100).

De verdeling van 1/6 kaas is een rationeel nummer.

De decimale expansie van een rationeel nummer eindigt altijd na een eindig aantal cijfers (bijv. 15,50) of wanneer dezelfde eindige reeks cijfers steeds opnieuw begint te worden herhaald (bijv. 0,345666666666666 ...). Daarom zijn de cijfers binnen de reeks rationele getallen opgenomen. Pure kranten of gemengde kranten.

Bovendien vertegenwoordigt elk herhaald of terminaal decimaal een rationeel aantal. Deze uitspraken zijn niet alleen waar voor basis 10, maar ook voor een ander basisnummer.

Een reëel getal dat niet rationeel is, wordt irrationeel genoemd. Irrationele getallen omvatten bijvoorbeeld √2, π en e. Omdat de hele reeks rationele getallen gevoelloos is en dat de groep reële getallen niet gevoelloos is, kan worden gezegd dat bijna alle reële getallen irrationeel zijn.

Rationele getallen kunnen formeel worden gedefinieerd als equivalentieklassen van hele paren (p, q) zodat q ≠ 0 of de equivalente relatie gedefinieerd door (p1, q1) (p2, q2) alleen als p1, q2 = p2q1.

De rationele getallen vormen, samen met de som en vermenigvuldiging, velden die de volledige getallen vormen en zijn opgenomen door een tak met geheel.

- Irrationele nummers

Irrationele getallen zijn allemaal reële getallen die geen rationele getallen zijn; Irrationele getallen kunnen niet worden uitgedrukt als breuken. De rationele getallen zijn de getallen die zijn samengesteld uit breuken van hele getallen.

Als gevolg van de zangeretest die zegt dat alle reële getallen niet -verwant zijn en dat het rationele als ze cijfers zijn, kan worden geconcludeerd dat bijna alle reële getallen irrationeel zijn.

Kan u van dienst zijn: traject en verplaatsing

Wanneer de straal van twee lijnsegmenten een irrationeel aantal is, kan worden gezegd dat deze lijnsegmenten onmetelijk zijn; wat betekent dat er onvoldoende lengte is, zodat elk van hen kan worden "meten" met een meervoudig geheel geheel.

Onder de irrationele getallen zijn de straal π van een cirkelcirkel naar zijn diameter, het aantal Euler (E), het gouden getal (φ) en de vierkantswortel van twee; Nog meer zijn alle vierkante wortels van natuurlijke nummers irrationeel. De enige uitzondering op deze regel zijn de perfecte vierkanten.

Opgemerkt kan worden dat wanneer irrationele getallen geplaatst worden uitgedrukt in een cijfersysteem (zoals decimale getallen) niet eindigen of herhalen.

Dit betekent dat ze geen reeks cijfers bevatten, de herhaling waardoor een lijn van representatie wordt gemaakt.

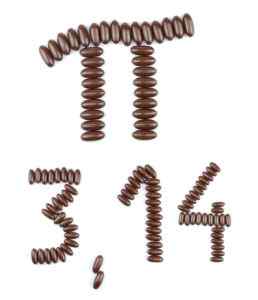Vereenvoudiging van het irrationele nummer pi.

Bijvoorbeeld: de decimale weergave van het nummer π begint met 3.14159265358979, maar er is geen eindig aantal cijfers dat π exact kan vertegenwoordigen, noch kunnen ze worden herhaald.

Het bewijs dat de decimale uitbreiding van een rationeel getal moet eindigen of herhalen is anders dan het bewijs dat een decimale extensie een rationeel getal moet zijn; Hoewel fundamenteel en enigszins lang, nemen deze tests wat werk aan.

Meestal nemen wiskundigen over het algemeen niet het idee van "eindigen of herhalen" om het concept van een rationeel nummer te definiëren.

Irrationele getallen kunnen ook worden behandeld via niet -continue breuken.

Referenties

1. Classifyng reële cijfers. Hersteld van chilimath.com.
2. Natuurlijk nummer. Hersteld van Wikipedia.borg.
3. Classificatie van getallen. Ditutor is hersteld.com.
4. Hersteld van Wikipedia.borg.
5. Irrationeel nummer. Hersteld van Wikipedia.borg.