Carnot -cyclusfasen, toepassingen, voorbeelden, oefeningen

Hij Carnotcyclus Het is de volgorde van thermodynamische processen die plaatsvinden in een carnotmotor, een ideaal apparaat dat alleen uit omkeerbare processen bestaat; dat wil zeggen degenen die, nadat ze hebben plaatsgevonden, kunnen terugkeren naar de beginstaat.

Dit type motor wordt als ideaal beschouwd, omdat het de dissipatie, wrijving of viscositeit ontbreekt die zich voordoet in echte machines, waardoor de thermische energie wordt veranderd in bruikbaar werk, hoewel de conversie niet 100% wordt uitgevoerd.

Figuur 1. Een stoomlocomotief. Bron: Pixabay

Een motor is gebouwd op basis van een stof die kan werken, zoals gas, benzine of stoom. Deze stof is onderworpen aan verschillende temperatuurveranderingen en ervaart op zijn beurt variaties in zijn druk en volume. Op deze manier is het mogelijk om een ​​zuiger in een cilinder te verplaatsen.

[TOC]

Wat is de carnotcyclus?

De carnotcyclus vindt plaats in een systeem genaamd Carnot of C -motor, een ideaal gas dat is vergrendeld in een cilinder en voorzien van een zuiger, die in contact staat met twee bronnen bij verschillende temperaturen t₁ en t₂ zoals die getoond in de volgende figuur links.

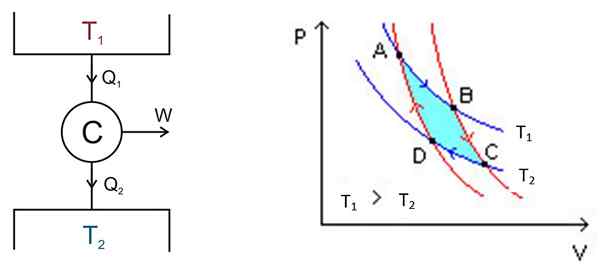Figuur 2. Links een schema van de C arnot -machine, rechts het PV -diagram. Bron van de linker figuur: keta - eigen werk, cc door 2.5, https: // commons.Wikimedia.org/w/index.PHP?Curid = 681753, rechterfiguur Wikimedia Commons.

Er zijn de volgende processen in een ruwe modus:

1. Een bepaalde hoeveelheid warmte wordt aan het apparaat geleverd_Ingang = Q₁ Van de thermische tank bij hoge temperatuur T₁.
2. De Carnot C -motor voert een werk uit dank aan deze verstrekte warmte.
3. Een deel van de gebruikte warmte: het afval Q_Uitgang, Het wordt overgebracht naar de thermische tank die zich bij een lagere temperatuur T bevat₂.

Carnot -cyclusfasen

De analyse wordt gemaakt door een P -V -diagram (druk -volume), zoals weergegeven in figuur 2 (rechterfiguur). Het doel van de motor kan zijn om de thermische afzetting 2 kou te houden, waardoor warmte uit het extraheren. In dit geval is het een Koelmachine. Als u integendeel de thermische afzetting wilt verwarmen 1, dan is het een Warmtepomp.

Het p -v -diagram toont drukveranderingen - motortemperatuur onder twee omstandigheden:

- Het handhaven van de constante temperatuur (isotherme proces).

- Geen warmteoverdracht (thermische isolatie).

De twee isothermische processen moeten worden aangesloten, wat wordt bereikt door middel van thermische isolatie.

Punt

U kunt op elk punt in de cyclus beginnen, waarbij gas bepaalde druk-, volume- en temperatuuromstandigheden heeft. Het gas lijdt een reeks processen en kan terugkeren naar de startomstandigheden om een ​​andere cyclus te beginnen, en altijd de uiteindelijke interne energie is hetzelfde als de initiële. Omdat energie wordt bewaard:

Werk gedaan door C = invoer warmte - vertrekwarmte

Δw = q_Ingang - Q_Uitgang

Het gebied dat is opgenomen in deze cyclus of lus, in turquoise in de figuur, is precies gelijk aan het werk dat door de Carnot -motor is gedaan.

Punten A, B, C en D zijn gemarkeerd in figuur 2. Het begint op het punt om de blauwe pijl te volgen.

Eerste fase: isothermische uitbreiding

De temperatuur tussen punten A en B is T₁. Het systeem absorbeert warmte van thermische afzetting 1 en lijdt een isotherme expansie. Dan neemt het volume toe en neemt de druk af.

De temperatuur blijft echter in t₁, Sinds wanneer het gas uitzet het koelt. Daarom blijft de interne energie ervan constant.

Het kan u van dienst zijn: Graff Van Generator: Partijen, hoe het werkt, applicaties

Tweede fase: adiabatische expansie

Op punt B begint het systeem een ​​nieuwe uitbreiding waarin het systeem niet wint of warmte verliest. Dit wordt bereikt door het in calorische isolatie te plaatsen zoals eerder aangegeven. Daarom is het een adiabatische uitbreiding die blijft wijzen op C na de rode pijl. Het volume neemt toe en de druk neemt af totdat het de laagste waarde bereikt.

Derde fase: isothermische compressie

Start bij punt C en eindig in D. De isolatie wordt verwijderd en het systeem komt in contact met thermische afzetting 2, waarvan de temperatuur T₂ Het is minder. Het systeem levert afvalwarmte op aan de thermische tank, de druk begint te stijgen en het volume om te verminderen.

Vierde fase: adiabatische compressie

Gereikt om punt D te bereiken, gaat het systeem terug naar thermische isolatie, de druk neemt toe en het volume neemt af totdat het bereiken van de oorspronkelijke omstandigheden van het punt a. Dan wordt de cyclus opnieuw herhaald.

Carnot's stelling

Carnot's stelling werd voor het eerst gepostuleerd in het begin van de 19e eeuw door de Franse natuurkundige Sadi Carnot. In het jaar 1824 publiceerde Carnot, die deel uitmaakte van het Franse leger, een boek waarin hij het antwoord op de volgende vraag stelde: onder welke omstandigheden een thermische machine heeft maximale efficiëntie? Carnot heeft vervolgens het volgende vastgesteld:

Geen thermische motor die tussen twee thermische afzettingen loopt, is efficiënter dan de Carnot -motor.

De η -opbrengst van een thermische motor wordt gegeven door de verhouding tussen het werk dat W en de geabsorbeerde warmte Q:

Prestaties = werk gedaan/geabsorbeerd warmte

Op deze manier is de prestaties van elke thermische motor I: η = w/q. Hoewel de prestaties van een Carnot R -motor η '= w/q' zijn, kunnen ze in het geval van beide motoren dezelfde taak uitvoeren.

Carnot's stelling stelt dat η nooit groter is dan η '. Anders valt het in tegenspraak met de tweede wet van de thermodynamica, volgens welke een proces waarbij het resultaat is dat warmte van een lichaam van lagere temperatuur onmogelijk is om naar een andere hogere temperatuur te gaan zonder externe hulp te ontvangen. Daarom:

η _< η^'

Carnot's stelling demonstratie

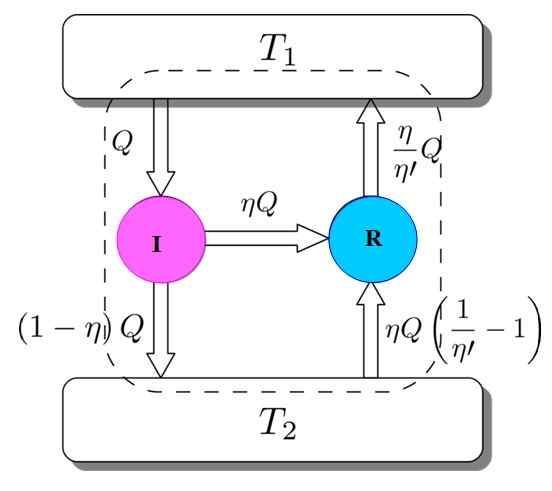
Om aan te tonen dat dit zo is, beschouw de Carnot -motor die werkt als een koelkastmachine aangedreven door een I -motor. Dit is mogelijk omdat de Carnot -motor werkt door omkeerbare processen, zoals aan het begin gespecificeerd.

figuur 3. Carnot's stelling demonstratie. Bron: Netheril96 [CC BY-SA 3.0 (https: // creativeCommons.Org/licenties/by-sa/3.0)]

Jullie hebben allebei: ik en r werken met dezelfde thermische afzettingen en er wordt aangenomen dat η _> η^'. Als onderweg een tegenstelling wordt bereikt met de tweede wet van de thermodynamica, wordt Carnot's stelling aangetoond door reductie tot absurditeit.

Figuur 3 helpt het proces te volgen. De I -motor neemt een hoeveelheid warmte Q, die op deze manier zich verdeelt: werk doen aan R equivalent aan w = ηq en de rest is de warmte overgebracht (1 -η) Q naar de thermische tank T₂.

Omdat de energie wordt bewaard, wordt alles vervuld:

EN_Ingang = Q = werk w + warmte toegewezen aan t₂ = ηq + (1 -η) q = e_Uitgang

Nu neemt de Carnot R -koelkastmachine de thermische tank 2 een hoeveelheid warmte gegeven door:

Het kan u van dienst zijn: Imantation: wat bestaat, methode en voorbeelden

(η / η ') (1 -η') q =

In dit geval moet ook energie worden bewaard:

EN_Ingang = ηq + (η / η ') (1 -η') q = (η / η ') q = q' = e_Uitgang

Het resultaat is de overdracht naar de thermische tank T₂ van een hoeveelheid warmte gegeven door (η / η ') q = q'.

Als η groter is dan η ', betekent dit dat de thermische afzetting met de hoogste temperatuur meer warmte is aangekomen dan ik oorspronkelijk heb genomen. Aangezien geen extern middel, zoals een andere thermische bron, heeft deelgenomen, is de enige manier waarop het kan gebeuren, dat de koudste thermische afzetting de warmte oplevert.

Dit is het niet eens met de tweede wet van de thermodynamica. Er wordt dan geconcludeerd dat het niet mogelijk is dat η^' Lager zijn dan η, daarom kan de I -motor niet meer prestaties hebben dan de carnot r -machine.

Stelling Corollary en beperkingen

De CARNOT -stelling Corollary stelt dat twee carnotmachines dezelfde efficiëntie hebben als beide werken met dezelfde thermische afzettingen.

Dat betekent dat de stof niet uitmaakt, de prestaties zijn onafhankelijk en kunnen niet worden verhoogd door deze te veranderen.

De conclusie van de vorige analyse is dat de carnotcyclus de top van het ideale haalbare thermodynamische proces is. In de praktijk zijn er veel factoren die de efficiëntie verminderen, bijvoorbeeld het feit dat isolatie nooit perfect is en in adiabatische fasen is er eigenlijk calorie -uitwisseling met de buitenkant.

In het geval van een auto wordt het motorkamer verwarmd. Aan de andere kant gedraagt ​​het gas- en luchtmengsel zich niet precies als een ideaal gas, het uitgangspunt van de carnotcyclus. Dit om slechts enkele factoren te noemen die een drastische prestatievermindering veroorzaken.

Voorbeelden

Een zuiger in een cilinder

Als het systeem een ​​zuiger is vergrendeld in een cilinder zoals in figuur 4, stijgt de zuiger tijdens de isothermische expansie, zoals te zien is in het eerste schema van de extreme links en stijgt ook tijdens de adiabatische expansie.

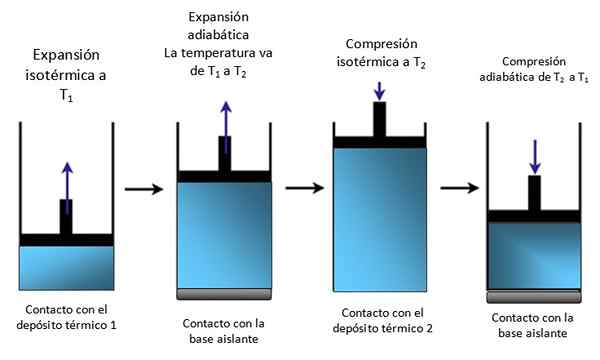Figuur 4. Beweging van een zuiger in een cilinder. Bron: zelf gemaakt.

Vervolgens isotherm gecomprimeerd, warmte geven en blijven adiabatisch comprimeren. Het resultaat is een beweging waarin de zuiger stijgt en naar beneden in de cilinder en kan worden overgebracht naar andere delen van een bepaald apparaat, zoals bijvoorbeeld een autorotemotor, die een paar produceert, of een stomende machine.

Verschillende omkeerbare processen

Naast de uitbreiding en compressie van een ideaal gas in een cilinder, zijn er andere ideale omkeerbare processen waarmee een carnotcyclus bijvoorbeeld kan worden geconfigureerd:

- Retourbewegingen in afwezigheid van wrijving.

- Een ideale veer die wordt gecomprimeerd en gedecomprimeerd en die nooit misvormingen zijn.

- Elektrische circuits waarin er geen weerstand is die energie afwijkt.

- Magnetisatie- en demagnetisatiecycli waarin er geen verliezen zijn.

- Een batterij laden en downloaden.

Een kerncentrale

Hoewel het een zeer complex systeem is, is een eerste benadering van wat nodig is om energie te produceren in kernreactor degene die volgt:

- Een thermische bron, bestaande uit een materiaal dat radioactief als uranium uiteenvalt.

Kan u van dienst zijn: huidige atoommodel

- De gootsteen of koude thermische afzetting die de atmosfeer zou zijn.

- De "carnot machine" die een vloeistof gebruikt, bijna altijd stromend water, dat warmte van de thermische bron wordt geleverd om het in stoom te veranderen.

Wanneer de cyclus wordt uitgevoerd, wordt elektriciteit verkregen als een netto werk. Wanneer getransformeerd in stoom op hoge temperatuur, wordt water bereikt tot een turbine, waarbij energie wordt omgezet in beweging of kinetische energie.

De turbine activeert op zijn beurt een elektrische generator die de energie van zijn beweging transformeert in elektriciteit. Naast het fistente materiaal zoals uranium, kunnen fossiele brandstoffen natuurlijk als warmtebron worden gebruikt.

Opgeloste oefeningen

-Voorbeeld 1: Efficiëntie van een thermische machine

De efficiëntie van een thermische machine wordt gedefinieerd als de verhouding tussen het outputwerk en het toegangswerk, en is daarom een ​​dimensieloze hoeveelheid:

Maximale efficiëntie = (q_Ingang - Q _Uitgang) /Q_Ingang

Het aangeven van maximale efficiëntie als E_maximaal, Het is mogelijk om zijn temperatuurafhankelijkheid aan te tonen, wat de gemakkelijkste variabele is om te meten, zoals:

En_maximaal = 1 - (T₂/T₁))

Waar T₂ Het is de temperatuur van de gootsteen en t₁ Het is de thermische brontemperatuur. Omdat het laatste groter is, blijkt de efficiëntie altijd minder te zijn dan 1.

Stel dat een thermische machine in staat is om op de volgende manieren te werken: a) tussen 200 K en 400 K, b) tussen 600 K en 400 K. Wat is de efficiëntie in elk geval?

Oplossing

a) In het eerste geval is de efficiëntie:

En_Max1 = 1 - (200/400) = 0.vijftig

b) Voor de tweede modus zal de efficiëntie zijn:

En_Max2 = 1- (400/600) = 0.33

Hoewel het temperatuurverschil hetzelfde is tussen beide modi, is de efficiëntie dat niet. En nog opmerkelijker is dat de meest efficiënte modus bij lagere temperatuur werkt.

-Voorbeeld 2: geabsorbeerde warmte en afgestudeerde warmte

Een thermische machine van 22 % produceert 1530 J werk. Zoek: a) De hoeveelheid warmte die wordt geabsorbeerd door thermische afzetting 1, b) de hoeveelheid warmte weggegooid naar thermische tank 2.

a) In dit geval wordt de efficiëntiedefinitie gebruikt, aangezien het werk dat is uitgevoerd, niet van de temperaturen van de thermische afzettingen beschikbaar is. Efficiëntie van 22% betekent dat E _Maximaal = 0.22, daarom:

Maximale efficiëntie = werk /q_Ingang

De hoeveelheid geabsorbeerde warmte is precies Q_Ingang, Dus je hebt vrijgemaakt:

Q_Ingang = Werk/efficiëntie = 1530 J/0.22 = 6954.5 J

b) De hoeveelheid warmte toegewezen aan de koudste tank is van δW = q_Ingang - Q_Uitgang

Q_Uitgang = Q_Ingang - ΔW = 6954.5 -1530 J = 5424.5 J.

Een andere manier is van En_maximaal = 1 - (T₂/T₁)). Omdat temperaturen niet bekend zijn, maar deze zijn gerelateerd aan warmte, kan efficiëntie ook worden uitgedrukt als:

En_maximaal = 1 - (Q_Bekledend/Q_geabsorbeerd))

Referenties

1. Bauer, W. 2011. Fysica voor engineering en wetenschappen. Deel 1. MC Graw Hill. 654-657
2. Kernenergie. Werking van een kerncentrale. Hersteld van: energie-nucleair.netto
3. Serway, r., Jewett, J. (2008). Natuurkunde voor wetenschap en engineering. Deel 1. 7e. ED. Cengage leren. 618-622.
4. Tippens, p. 2011. Fysica: concepten en toepassingen. 7e editie. MacGraw Hill. 414-416.
5. Walker, J.2008. Natuurkunde. 4e ed.Addison Wesley. 610-630